文章目錄
- 一、算法原理
- 二、案例分析
- 2.1 構建指標層判斷矩陣
- 2.2 求各指標權重
- 2.2.1 算術平均法(和積法)
- 2.2.2 幾何平均法(方根法)
- 2.3 一致性檢驗
- 2.3.1 求解最大特征根值
- 2.3.2 求解CI、RI、CR值
- 2.3.3 一致性判斷
- 2.4 分別求解方案層權重向量及一致性檢驗
- 2.4.1 景色
- 2.4.2 吃住
- 2.4.3 價格
- 2.4.4 人文
- 2.5 計算各方案得分
- 三、python 代碼
- 3.1 和積法計算權重
- 3.2 方根法計算權重
- 3.3 python庫 np.linalg.eig
一、算法原理
-
層次分析法(analytic hierarchy process),簡稱AHP,是指將與決策總是有關的元素分解成目標、準則、方案等層次,在此基礎之上進行定性和定量分析的決策方法。該方法是美國運籌學家匹茨堡大學教授薩蒂于20世紀70年代初,在為美國國防部研究"根據各個工業部門對國家福利的貢獻大小而進行電力分配"課題時,應用網絡系統理論和多目標綜合評價方法,提出的一種層次權重決策分析方法。
-
傳統定性分析方法類似專家打分、專家判斷等,僅能將指標簡單地劃分為幾個層級(類似非常重要、比較重要、一般、比較不重要、非常不重要),這樣導致部分存在差別但是不大的指標得到了同樣的權重,受主觀因素影響,無法對最終決策做出更好的幫助。層次分析法將不同指標間一一比對,主觀與客觀相結合,很好地解決了以上問題。
-
判斷矩陣量化值參照表:
| 因素i比因素j | 量化值 |
|---|---|
| 同等重要 | 1 |
| 稍微重要 | 3 |
| 較強重要 | 5 |
| 強烈重要 | 7 |
| 極端重要 | 9 |
| 兩相鄰判斷的中間值 | 2,4,6,8 |
| 倒數 | 假設因素i相比因素j重要程度量化值為3,相反就是1/3 |
二、案例分析
目的:選擇某個城市旅游
方案:南京、桂林、三亞
考慮因素:景色、吃住、價格、人文
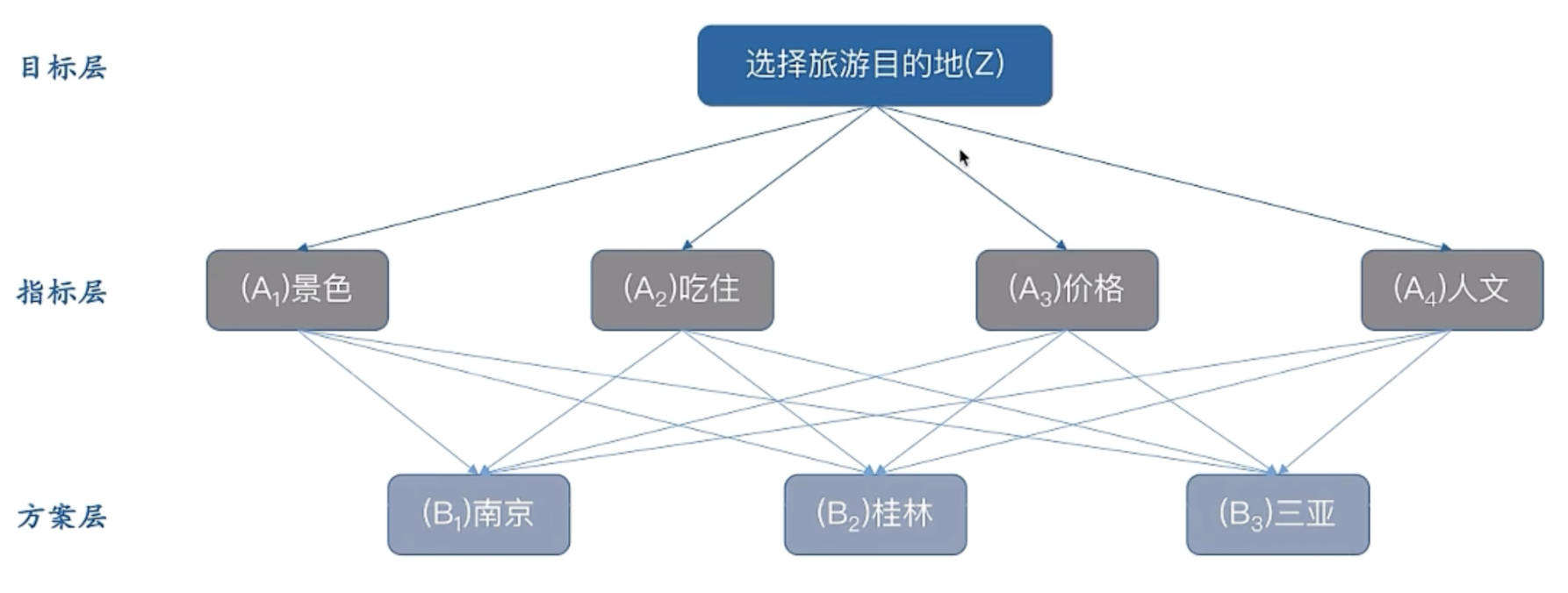
2.1 構建指標層判斷矩陣

構建判斷矩陣,理論上需要專家打分。
2.2 求各指標權重
2.2.1 算術平均法(和積法)
-
按列求和:如 1 + 4 + 1 / 2 + 3 = 8.5 1+4+1/2+3 = 8.5 1+4+1/2+3=8.5。
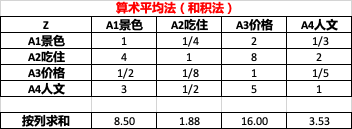
-
將指標層判斷矩陣按列歸一化(即按列求占比),如:
0.12 = 1 / 8.5 0.12 = 1 / 8.5 0.12=1/8.5
0.47 = 4 / 8.5 0.47 = 4 / 8.5 0.47=4/8.5
0.06 = 1 / 2 / 8.5 0.06 = 1/2 / 8.5 0.06=1/2/8.5
0.35 = 3 / 8.5 0.35 = 3 / 8.5 0.35=3/8.5

-
將歸一化后的矩陣按行求平均,得到權重向量w

2.2.2 幾何平均法(方根法)
-
每行各元素相乘(行乘積),如 1 ? 1 / 4 ? 2 ? 1 / 3 = 0.1667 1*1/4*2*1/3 = 0.1667 1?1/4?2?1/3=0.1667
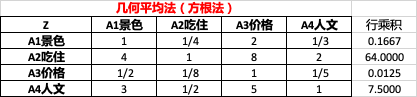
-
對乘積列每個元素開n次方(n為矩陣階數,此處n=4),如 0.1667 4 = 0.6389 \sqrt[4]{0.1667}=0.6389 40.1667?=0.6389.

-
然后對開方列求列占比,得到權重向量w,如 0.1171 = 0.6389 / 5.4566 0.1171=0.6389 / 5.4566 0.1171=0.6389/5.4566.

2.3 一致性檢驗
2.3.1 求解最大特征根值
得到權重向量后,可以計算出原判斷矩陣的最大特征根值,公式為:
λ m a x = 1 n ∑ i = 1 n ( A W i ) W i \lambda_{max}=\dfrac{1}{n}\sum_{i=1}^{n}{\dfrac{(AW_{i})}{W_{i}}} λmax?=n1?i=1∑n?Wi?(AWi?)?
其中,n為矩陣階數,此處n=4。
求解步驟(以和積法求解權重為例)
-
求 A W AW AW,其中 0.4705 = 1 ? 0.1176 + 1 4 ? 0.5175 + 2 ? 0.0611 + 1 3 ? 0.3038 0.4705=1*0.1176+\dfrac{1}{4}*0.5175+2*0.0611+\dfrac{1}{3}*0.3038 0.4705=1?0.1176+41??0.5175+2?0.0611+31??0.3038

-
求 A W W \dfrac{AW}{W} WAW?,如 4.0016 = 0.4705 / 0.1176 4.0016=0.4705/0.1176 4.0016=0.4705/0.1176
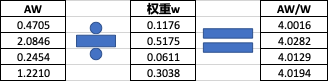
-
求 1 n s u m ( A W W ) \dfrac{1}{n}sum(\dfrac{AW}{W}) n1?sum(WAW?),此處 s u m ( A W W ) = 16.0621 sum(\dfrac{AW}{W})=16.0621 sum(WAW?)=16.0621

-
綜上求得 λ m a x = 1 4 ? 16.0621 = 4.0155 \lambda_{max}=\dfrac{1}{4}*16.0621=4.0155 λmax?=41??16.0621=4.0155。
2.3.2 求解CI、RI、CR值
- 計算CI
C I = λ ? n n ? 1 = 4.0155 ? 4 4 ? 1 = 0.0052 CI=\dfrac{\lambda-n}{n-1}=\dfrac{4.0155-4}{4-1}=0.0052 CI=n?1λ?n?=4?14.0155?4?=0.0052
- 計算RI
根據查表,得知 R I RI RI為0.89

- 計算CR
C R = C I R I = 0.0052 0.89 = 0.0058 CR=\dfrac{CI}{RI}=\dfrac{0.0052}{0.89}=0.0058 CR=RICI?=0.890.0052?=0.0058
2.3.3 一致性判斷
CR = 0.0058 < 0.1,即通過一致性檢驗。
2.4 分別求解方案層權重向量及一致性檢驗
2.4.1 景色
-
構建判斷矩陣
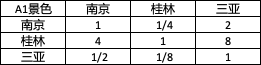
-
計算權重向量以及一致性檢驗.(步驟如上文,為了簡便文章,本次計算采用python代碼,以和積法求解權重,下文將詳細介紹)

2.4.2 吃住
-
構建判斷矩陣
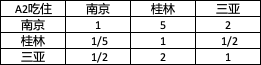
-
計算權重向量以及一致性檢驗.(步驟如上文,為了簡便文章,本次計算采用python代碼,以和積法求解權重,下文將詳細介紹)

2.4.3 價格
-
構建判斷矩陣
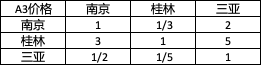
-
計算權重向量以及一致性檢驗.(步驟如上文,為了簡便文章,本次計算采用python代碼,以和積法求解權重,下文將詳細介紹)

2.4.4 人文
-
構建判斷矩陣
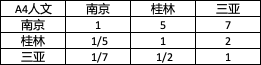
-
計算權重向量以及一致性檢驗.(步驟如上文,為了簡便文章,本次計算采用python代碼,以和積法求解權重,下文將詳細介紹)

2.5 計算各方案得分
綜合得分 = s u m ( 單項得分 ? 對應指標權重 ) 綜合得分=sum(單項得分*對應指標權重) 綜合得分=sum(單項得分?對應指標權重)

可以看出,南京得分0.5675為最高,最終方案應選擇南京。
三、python 代碼
3.1 和積法計算權重
import numpy as np
import pandas as pd''' 層次分析法判斷矩陣權重向量計算--和積法 '''
def get_w_anc(factors_matrix):# RI字典RI_dict = {1:0,2:0,3:0.52,4:0.89,5:1.12,6:1.26,7:1.36,8:1.41,9:1.46,10:1.49,11:1.52,12:1.54,13:1.56,14:1.58,15:1.59}# 矩陣階數shape = factors_matrix.shape[0]# 按列求和column_sum_vector = np.sum(factors_matrix, axis=0)# 指標層判斷矩陣歸一化normalization_matrix = factors_matrix / column_sum_vector# 按行求歸一化后的判斷矩陣平均值,得到權重WW_vector = np.mean(normalization_matrix, axis=1)# 原判斷矩陣 乘以 權重向量AW_vector = np.dot(factors_matrix, W_vector)# 原判斷矩陣 ?? 權重向量 / 權重AW_w = AW_vector / W_vector# 求特征值lamda = sum(AW_w) / shape# 求CI值CI = (lamda - shape) / (shape - 1)# 求CR值CR = CI / RI_dict[shape]print("權重向量為:",list(W_vector))print("最大特征值:",lamda)print("CI值為:",CI)print("RI值為:",RI_dict[shape])print("CR值為:",CR)if CR < 0.1:print('矩陣通過一致性檢驗')else:print('矩陣未通過一致性檢驗')print("---------------------------")return W_vectorif __name__ == "__main__":# 指標層判斷矩陣factors_matrix = np.array([[1,1/4,2,1/3],[4,1,8,2],[1/2,1/8,1,1/5],[3,1/2,5,1]])# 景色view_matrix = np.array([[1,1/4,2],[4,1,8],[1/2,1/8,1]])# 吃住board_matrix = np.array([[1,5,2],[1/5,1,1/2],[1/2,2,1]])# 價格price_matrix = np.array([[1,1/3,2],[3,1,5],[1/2,1/5,1]])# 人文humanity_matrix = np.array([[1,5,7],[1/5,1,2],[1/7,1/2,1]])w_A = get_w_anc(factors_matrix)print("景色:")w_view = get_w_anc(view_matrix)print("吃住:")w_board = get_w_anc(board_matrix)print("價格:")w_price = get_w_anc(price_matrix)print("人文:")w_humanity = get_w_anc(humanity_matrix)# 將景色、吃住、價格、人文權重向量合并w_B = np.vstack((w_view, w_board,w_price,w_humanity))# 求出最終得分score = np.dot(w_A,w_B)print("最終得分向量:",score)
- 運行結果

3.2 方根法計算權重
這里只列出計算權重部分
- 原指標層判斷矩陣
# 指標層判斷矩陣
factors_matrix = np.array([[1,1/4,2,1/3],[4,1,8,2],[1/2,1/8,1,1/5],[3,1/2,5,1]
])
- 求行乘積
# 求行乘積
array1 = factors_matrix.prod(axis=1, keepdims=True)
- 對乘積列每個元素開n次方(n為矩陣階數,此處n=4)
n = 4
array2 = np.power(array1, 1/n)
- 對開方列求列占比,得到權重向量w
array2 / np.sum(array2)
3.3 python庫 np.linalg.eig
# 計算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(factors_matrix)# 需要注意的是,對于一個nxn的矩陣,最多可能有n個特征值和特征向量,因此,需要挑選出最大的特征值進行一致性判斷
# 找到最大特征值的索引
max_eigenvalue_index = np.argmax(eigenvalues)# 提取最大特征值和對應的特征向量
max_eigenvalue = eigenvalues[max_eigenvalue_index]
max_eigenvector = eigenvectors[:, max_eigenvalue_index]print("最大特征值:", max_eigenvalue)
print("對應的特征向量:", max_eigenvector)
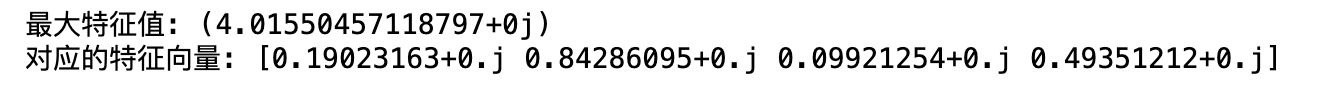
- 參考:層次分析法(AHP)步驟詳解-嗶哩嗶哩
- 參考:層次分析法原理及計算過程詳解)



)





函數)

)

)





