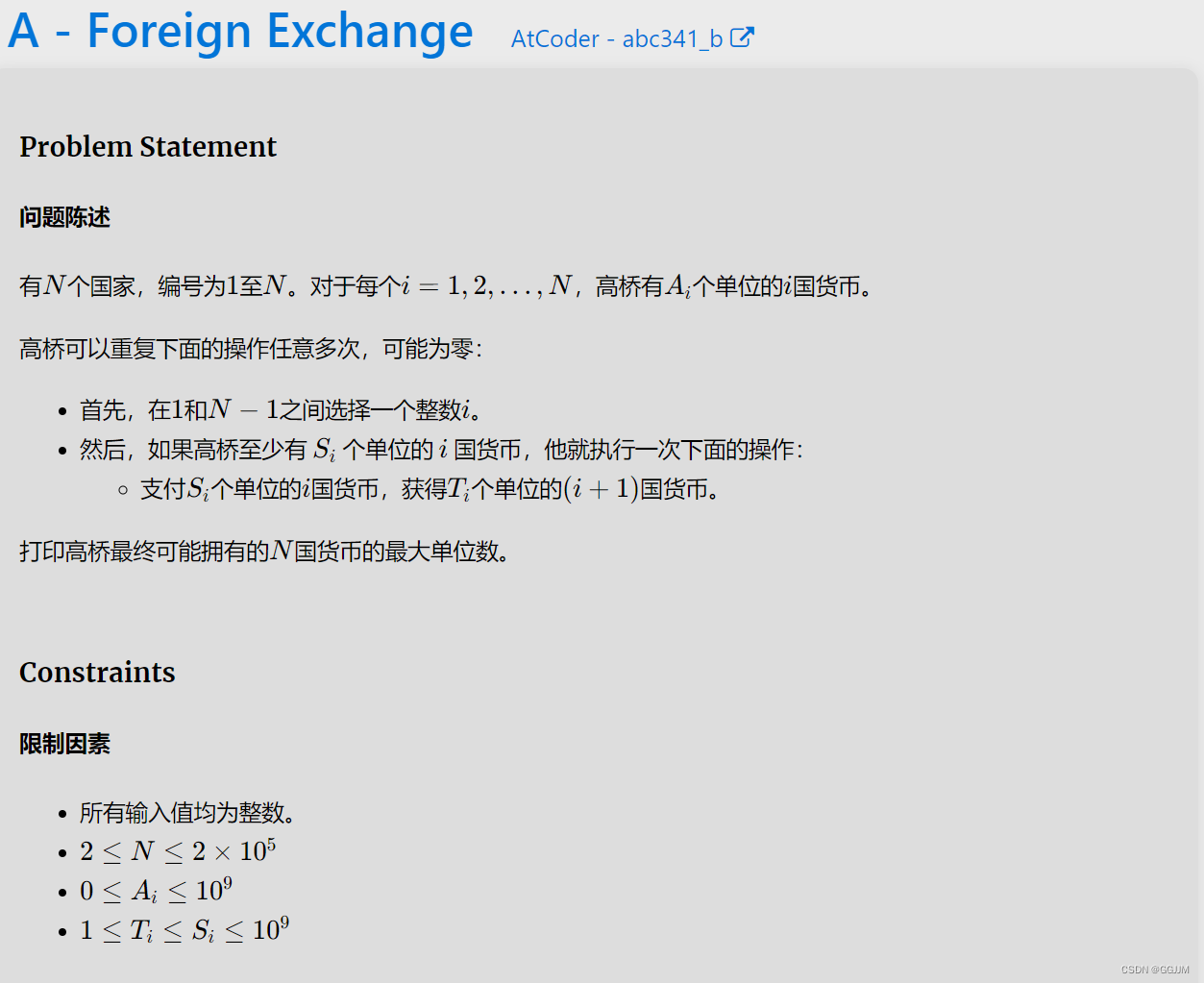
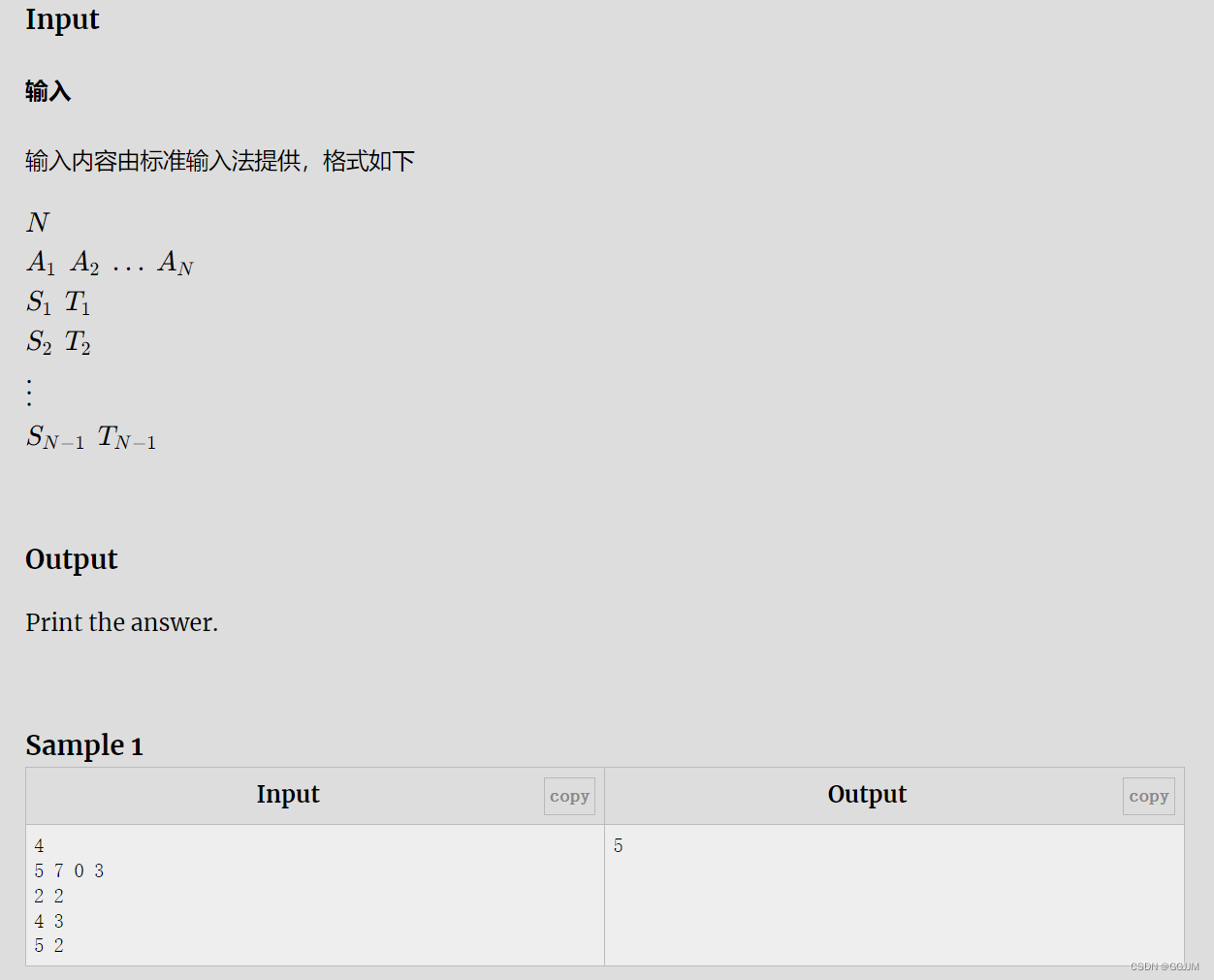
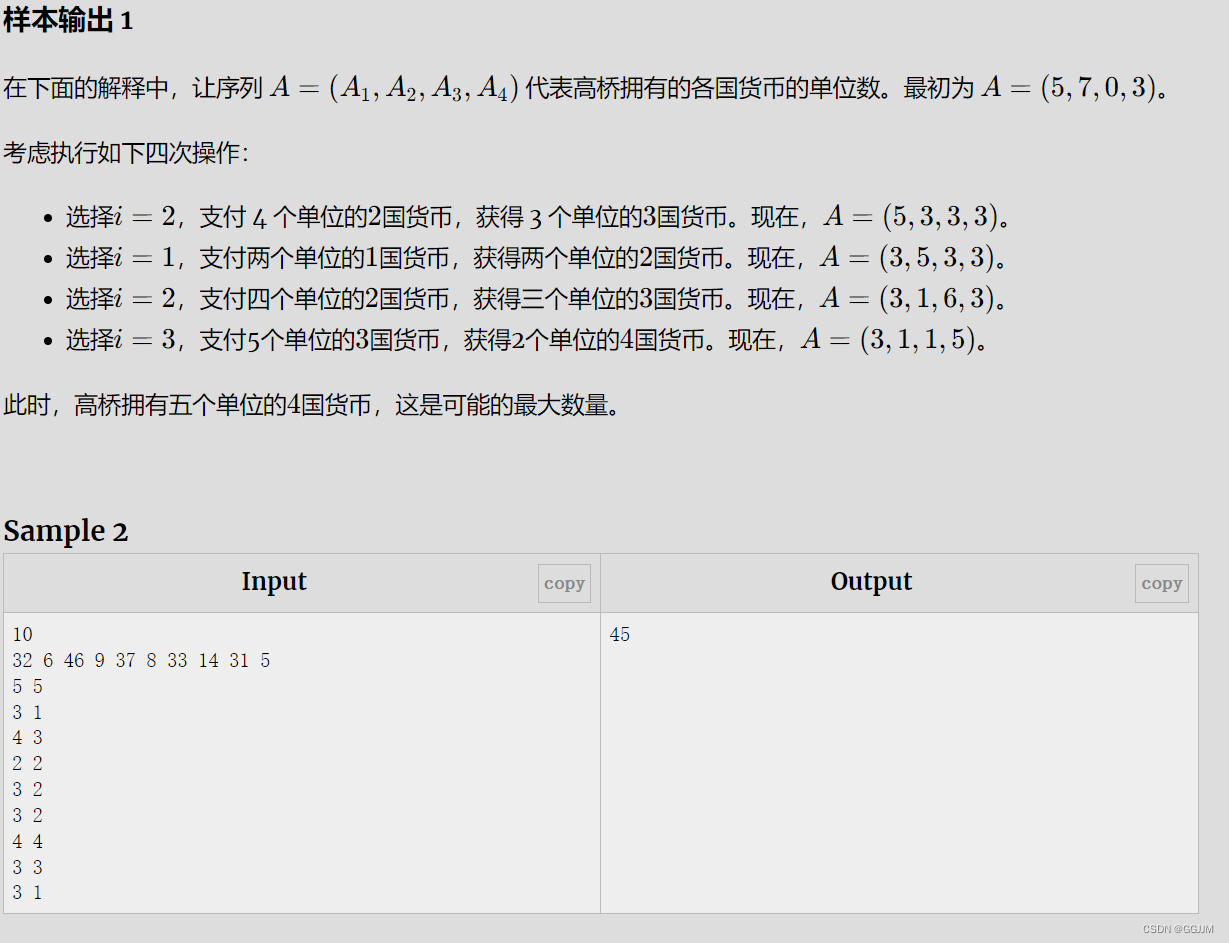
解題思路
簡單模擬。
代碼
#include <bits/stdc++.h>
using namespace std;
long long g[2000000];
long long n;
int main()
{long long x,y,z,sum=0,k=0;scanf("%lld",&n);for(x=1;x<=n;x++)scanf("%lld",&g[x]);for(x=1;x<n;x++){scanf("%lld%lld",&y,&z);k=g[x]/y;g[x+1]+=z*k;}printf("%lld",g[x]);return 0;
}
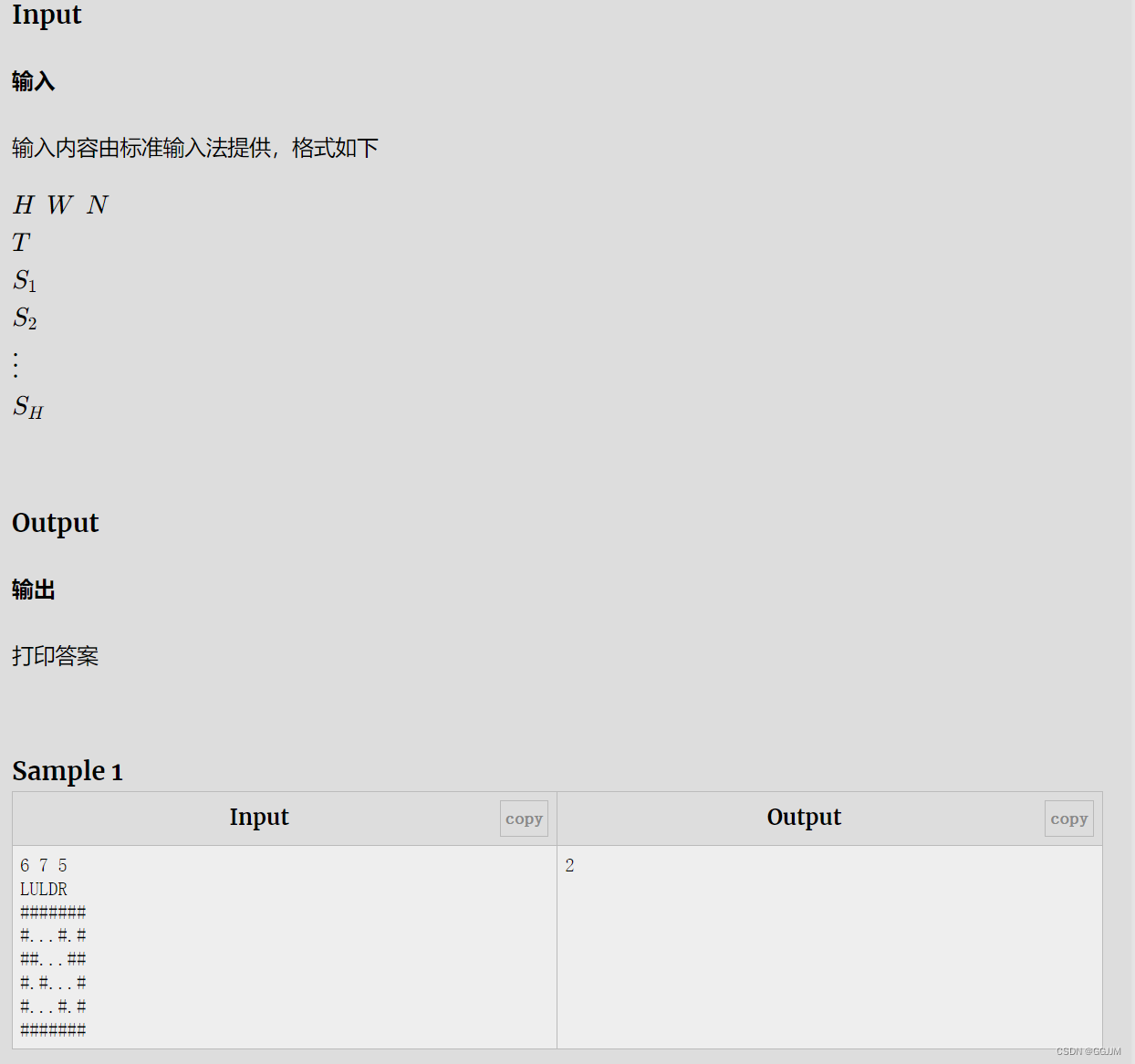

解題思路
運用dfs的方法,但搜索方向和順序都是固定的。
代碼
#include <bits/stdc++.h>
using namespace std;
char g[510][510];
int h,w,n;
char t[510];
int m[510];
int ne[5][2]={{0,0},{1,0},{0,1},{-1,0},{0,-1}};
int main()
{int x,y,z,l,r,tx,ty,sum=0;scanf("%d%d%d",&h,&w,&n);scanf("%s",t);for(x=0;t[x]!='\0';x++){switch(t[x]){case 'L':m[x]=4;break;case 'U':m[x]=3;break;case 'R':m[x]=2;break;case 'D':m[x]=1;break;}}for(x=1;x<=h;x++){getchar();scanf("%s",g[x]+1);}for(x=1;x<=h;x++){for(y=1;y<=w;y++){if(g[x][y]=='.'){l=x;r=y;for(z=0;z<n;z++){tx=l+ne[m[z]][0];ty=r+ne[m[z]][1];if(g[tx][ty]!='.')break;l=tx;r=ty;}if(z==n)sum++;}}}printf("%d",sum);return 0;
}

解題思路
排序一下然后模擬就行了。
代碼
#include <bits/stdc++.h>
using namespace std;
long long g[110];
int main()
{long long t,n,sum=0;long long x,y,z;scanf("%d",&t);for(x=0;x<t;x++){sum=0;scanf("%lld",&z);for(y=1;y<=z;y++)scanf("%lld",&g[y]);sort(g+1,g+z+1);for(y=1;y<z;y++)sum+=g[y+1]-g[y];printf("%lld\n",sum);}return 0;
}

解題思路
運用并查集來模擬連接各個村子,然后檢查有幾個城鎮沒有鏈接就將它鏈接就行了(要小心多棵樹出現的情況)。
代碼
#include <bits/stdc++.h>
using namespace std;
int j[1010];
struct ss
{int x;int y;
}g[1010*1010];
int find1(int x)
{if(j[x]==x)return x;return j[x]=find1(j[x]);
}
void unit(int x,int y)
{j[find1(y)]=find1(x);
}
void sset(int b)
{for(int x=1;x<=b;x++)j[x]=x;
}
int main()
{int n,m;int x,y,z,sum;while(1){scanf("%d",&n);if(n==0)break;sset(n);sum=0;scanf("%d",&m);for(x=0;x<m;x++){scanf("%d%d",&g[x].x,&g[x].y);if(find1(g[x].x)!=find1(g[x].y)){unit(g[x].x,g[x].y);}}for(x=2;x<=n;x++){if(find1(1)!=find1(x)){unit(1,x);sum++;}}printf("%d\n",sum);}return 0;
}# [藍橋杯 2013 省 B] 翻硬幣
## 題目背景
小明正在玩一個“翻硬幣”的游戲。
## 題目描述
桌上放著排成一排的若干硬幣。我們用 `*` 表示正面,用 `o` 表示反面(是小寫字母,不是零),比如可能情形是 `**oo***oooo`,如果同時翻轉左邊的兩個硬幣,則變為 `oooo***oooo`。現在小明的問題是:如果已知了初始狀態和要達到的目標狀態,每次只能同時翻轉相鄰的兩個硬幣,那么對特定的局面,最少要翻動多少次呢?
## 輸入格式
兩行等長字符串,分別表示初始狀態和要達到的目標狀態,每行長度小于 1000。
數據保證一定存在至少一種方案可以從初始狀態和要達到的目標狀態。
## 輸出格式
一個整數,表示最小操作步數。
## 樣例 #1
### 樣例輸入 #1
```
**********
o****o****
```
### 樣例輸出 #1
```
5
```
## 樣例 #2
### 樣例輸入 #2
```
*o**o***o***
*o***o**o***
```
### 樣例輸出 #2
```
1
```
代碼
#include <bits/stdc++.h>
using namespace std;
char g[1010];
char j[1010];
int main()
{int x,y,z=0;scanf("%s%s",g,j);for(x=0;g[x]!='\0';x++){if(g[x]!=j[x]){g[x]=j[x];if(g[x+1]=='*')g[x+1]='o';elseg[x+1]='*';z++;}}printf("%d",z);return 0;
})


)







-ControlNet(線稿約束))


)




