移相電路就是對輸入信號(一般是正弦波)進行相位控制，而不改變其幅度，本推文以移相電路為例，展示模擬電路的反饋設計技巧與方法：
一、全通濾波器實現移相

以上是兩種移相電路 的原理，其輸出幅度保持不變，移動的相位隨R3和C而改變，在C和R3確定時其移相是arctan函數，非線性的，當WR3C較小時，近似線性arctan(x)=x,|x|<=0.5，仿真伯德特的相位如下：

上圖可見，在WR3C較小時，是線性相移，即確定最最高頻率Wmax后可以反向計算R3C<=0.5/Wmax,確定線性相移應用的時間常數R3C。

二、反饋控制設計舉例
現在需要設計一個電路，實現輸入頻率在一定范圍內變化、輸入信號的初始相位變化時，輸出信號始終超前輸入信號90°，而輸出信號幅度保持與輸入信號幅度相同。這該如何實現？

應用前述的全通濾波器，好像有希望實現，關鍵是要能調整C與R3,而且要剛好調整到對輸入信號移相90°，這是問題的關鍵。我們把問題細分一下：

1）如何改變C或R3？
2) 如何檢測相位差？這其實就是要根據相位差來反饋控制C或R3的變化，可以采用模擬控制也可用數字控制方式。

先說1），改變C當然不能人去手動調節，要用電信號自動調節，首先想到的就是反向偏置的變容二極管,本推文我們不選擇改變C，如果是改變R3那么如何做？當然不能用普通電位器了

，我們還是需要能電控改變阻值的東東：

a）不少人可能首先想到的是數字電位器，這個有些問題：首先太復雜，意味著你要使用單片機，而且數字電位器都是離散電阻值，假設一步對應100歐姆，1.5khz時需要900歐姆，剛好合適，而1.525khz輸入頻率，如果需要923.56歐，就完了，因為一步對應100歐姆的數字電位器只有900歐姆、1000歐姆，沒有923.56歐姆，會影響控制精度，所以數字電位器不是最佳方案。那么你非要使用數字電位器又該怎么辦？那也不是沒有辦法，只是精度差一些：比如，你可以參考PWM控制的思路，在20次控制中，1000*(20-x)/20+900*x/20=923.56,計算出x次選擇900歐，剩下(20-x)選擇1000歐。

b）還有就是選擇JFET管，工作在可變電阻區，這是非常好的方案，只是要控制JFET的工作電壓和擴展JFET的線性，下面詳述

再說2），這里關鍵是需要一個鑒相器，來檢測相位差，二極管鑒相器、二極管平衡環狀鑒相器、乘法器....都可以做鑒相器，這里為了簡單選擇乘法器做鑒相器

先給出整體仿真電路和仿真實驗結果：

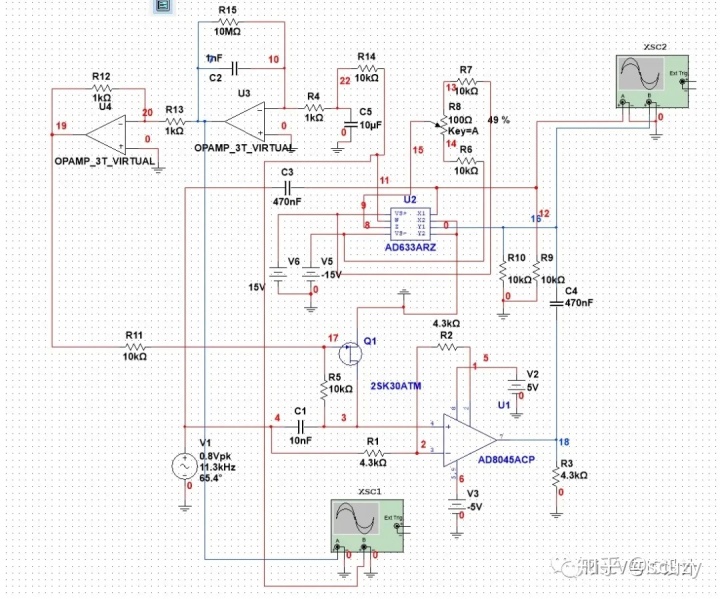
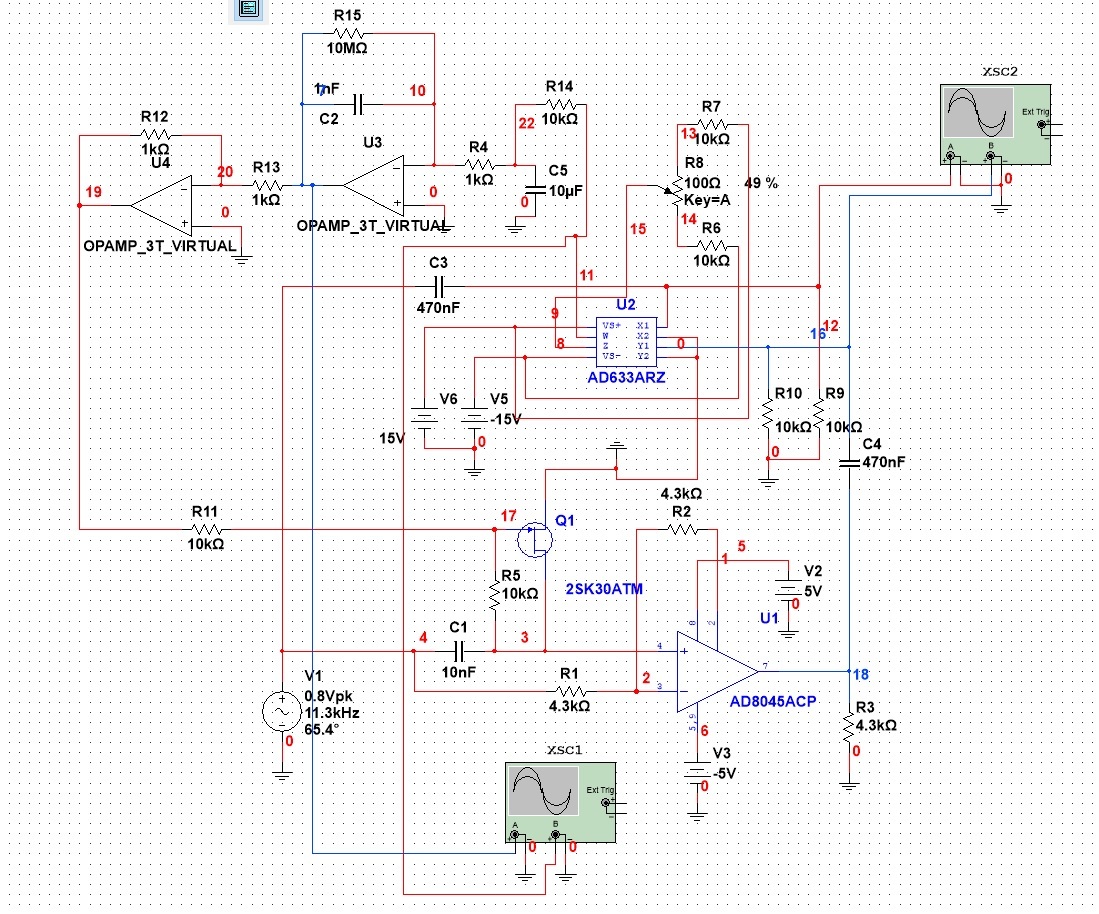
下面看看反饋跟蹤控制電路，其由鑒相器和JFET可變電阻構成：

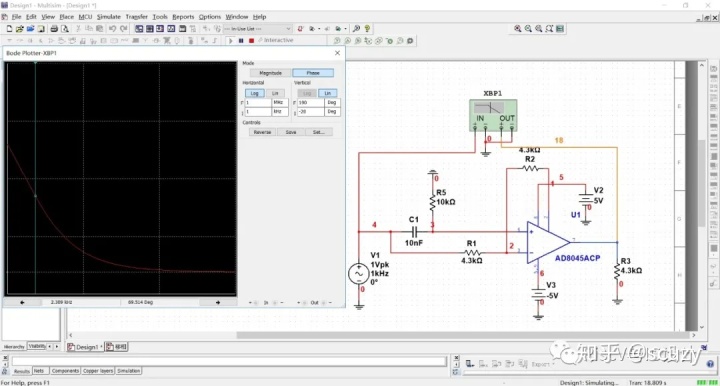
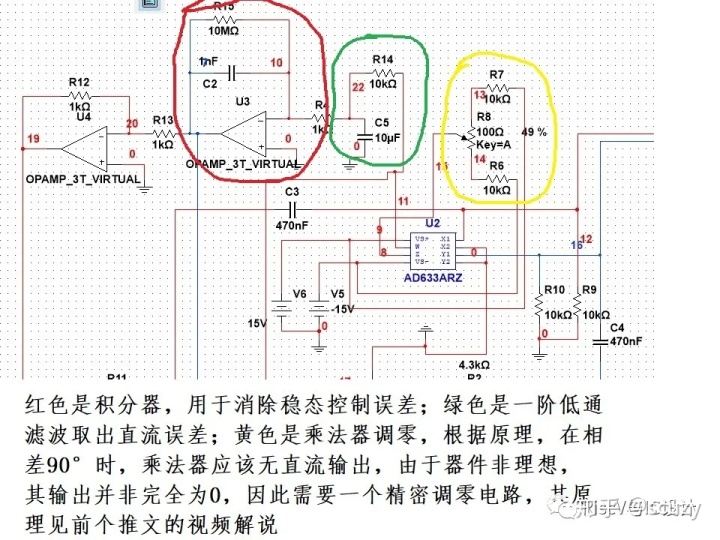
1）鑒相器這里采用的是乘法器，把輸出信號Asin(wt+Po)與輸入信號Asin(wt+P1)相乘，sina*sinb=-0.5[cos(a+b)-cos(a-b)],當兩者差90°時結果只有cos2wt 二倍頻分量，無直流分量,而非90°相位差時，會有一個直流分量0.5*cos(Po-P1), 推文中使用一個一階RC取出直流分量，然后對直流分量進行積分，這個積分器是必須的，其作用就是如果誤差沒有消除就不斷增強調節作用，此處如果換成放大器就沒有持續調節作用了，其實這就是PID控制中的積分環節，目的就是消除最終的穩態誤差！此電路只是臨時起意設計的，參數還沒有優化計算。

2）JFET可變電阻

jFET的輸出電流ID與VGS(柵源電壓)、VDS(漏源電壓)關系如下，可以推導出其輸出導納gDS

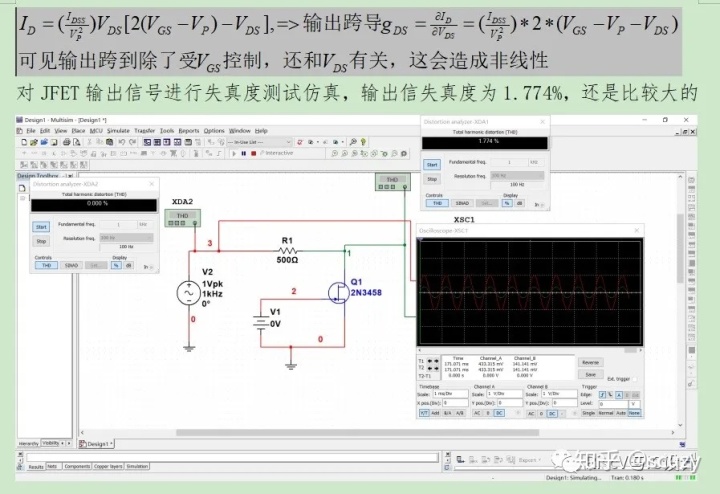
現在如下圖所示，通過R3/R2引入對Vds信號的反饋，目的是減小JFET輸出電阻的非線性，造成非線性的原因從上圖的gDS公式可見其還是Vds的函數，因此我們的做法還是負反饋！引入對Vds信號的負反饋來抑制Vds對ID的影響！

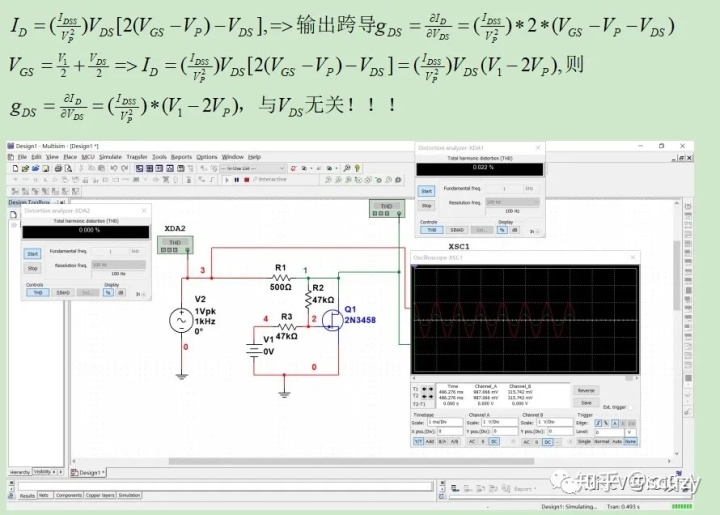
失真補償以后，失真度降為0.022%，這改善非常明顯，記住善于應用負反饋者，如果模擬電路世界的天下一分為四，你已得其一！是不是有點當年諸葛大神的隆中對三分天下的意思？

這種JFET低失真可變電阻很有用，例如下圖的低失真系數的正弦波振蕩器：

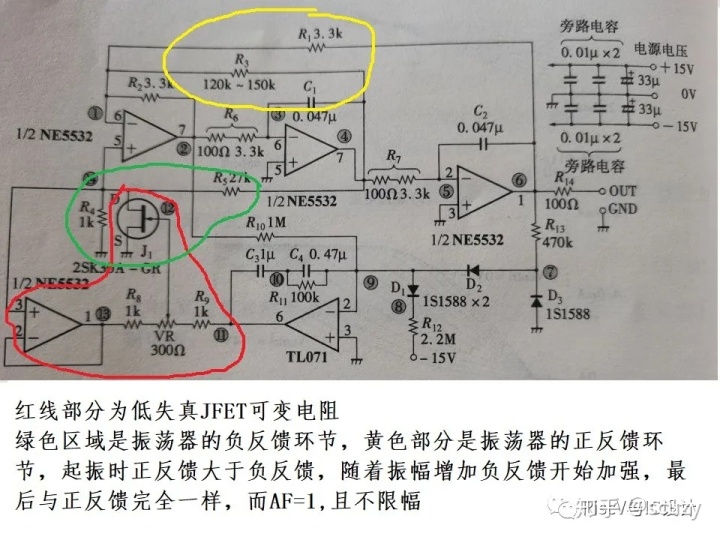
紅色區域左下角的1:1運放就是為了隔離R8/R9/VR對R4的負載效應; TL071也是反饋控制中的積分環節，目的一樣是消除穩態誤差；D2/D3構成主要的信號幅度信息提取網絡，采用半波整流電路取出正半周信號，通過積分器其實就是半波整流輸出信號的平均直流分量，該分量與正弦波的幅度成比例：

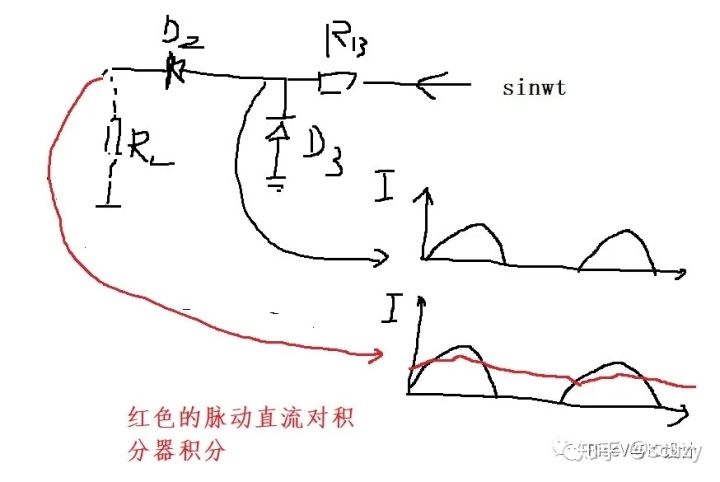
二極管半波整流雖然簡單而且不精確，但是和積分器搭配卻是很常見的信號幅度提取與反饋控制的手段！

關注微信公眾號: RiscV與IC設計