文章目錄

• 寫在前面
• 1. 從幾何變換到奇異值分解
• 2. 代數角度理解奇異值與奇異向量
  • 2.1 從正交基映射推導SVD
  • 2.2 特征值分解求解奇異值和奇異向量
    • 2.2.1 求解過程
    • 2.2.2 推論
  • 2.3 SVD的另一種形式
• 3. 幾何角度理解奇異值與奇異向量
  • 3.1 從坐標變換理解
    • 3.1.1 從例子到一般
    • 3.1.2 兩個問題
  • 3.2 形變的角度理解奇異值
• 4. 我覺得的最好的奇異值解讀
• 5. 特征值分解和奇異值分解區別
• 6. 奇異值分解在PCA中的應用
• 參考文獻

寫在前面

讀完本篇文章后，你應該可以知道：

奇異值分解到底是什么？
奇異值和奇異向量有什么代數意義？
奇異值和奇異向量有什么幾何意義？
如何利用特征值分解求奇異值和奇異向量？
奇異值的個數如何確定？
奇異值分解是否唯一？
奇異值分解什么時候和特征值分解相等？
奇異值分解和特征值分解的區別？

1. 從幾何變換到奇異值分解

這部分的內容是[1]中部分內容的翻譯，這幾張圖片大家應該見過很多次。

來看一個二維平面坐標系的例子，在由(1,0)T和(0,1)T確定的二維平面坐標系中：

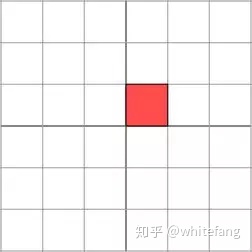
向量(x,y)T左乘M矩陣，將會得到一個新的向量(新的點)。為了更容易理解變換過程，我們主要關注向量(1,1)T和(1,0)T,(0,1)T,(0,0)T圍城的矩形的形變過程。

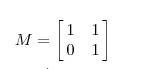
左乘矩陣M的效果在坐標系中的表現如下：

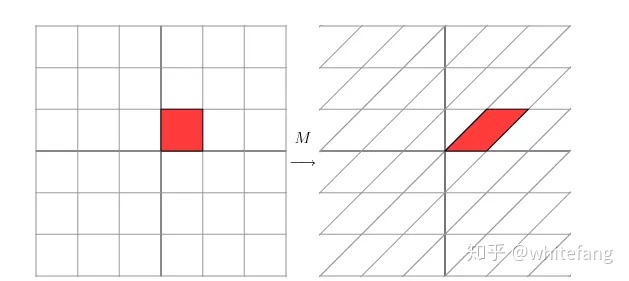
直接從圖上看不出什么，我們把原先的坐標系逆時針旋轉30度，然后左乘M看看效果：

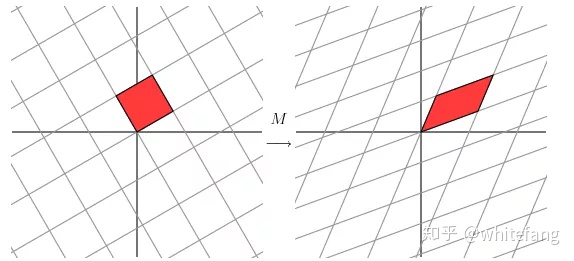
好像也沒什么特殊的，把原先的坐標系逆時針旋轉60度看看：

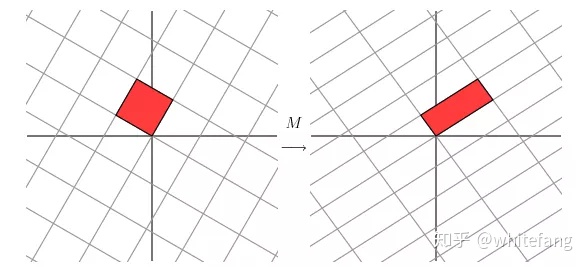
右邊的網格幾乎快要正交了，也就是說，原先的正交基逆時針旋轉60度后，再經過M變換，幾乎可以得到一組新的正交基。

實際上，如果我們把坐標軸逆時針旋轉58.28度，就會得到如下效果：

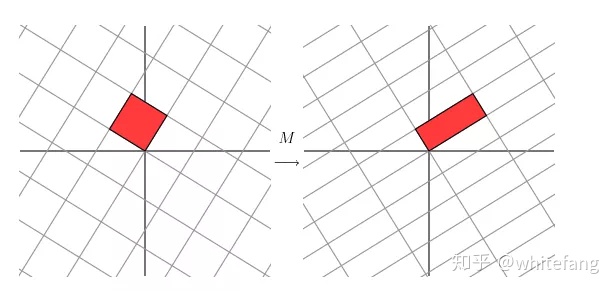
從幾何上看，旋轉后的正交基(1,0)T和(0,1)T，在經過M變換后，得到了另外一組正交基。這其實就是SVD分解的一種解釋，即M可以將一組正交基映射到另一組正交基。

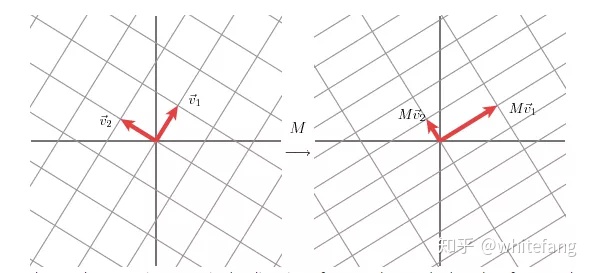
記映射后的向量Mv1為u1,Mv2為u2,Mv1的模為σ1，Mv2的模為σ2。

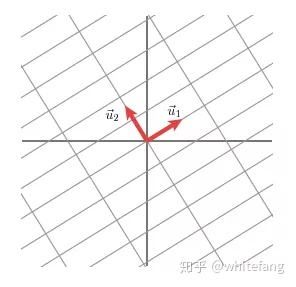
接下來我們就可以推導了：

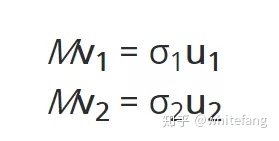
在v1和v2確定的二維平面中，任意一點x可以表示為：

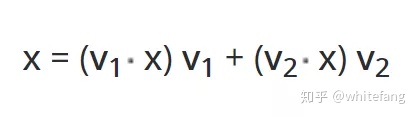
在《利用SVD進行推薦（1）矩陣相乘的本質》中我們講過，小括號里的點積就是x在v1和v1坐標軸上的投影值(坐標)。我們對這個平面中任意一點x左乘矩陣M進行變換，來看看結果：

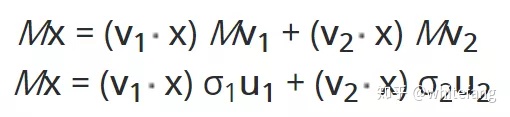
向量點積表示為矩陣乘法就是：

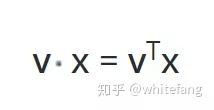
所以變換結果可以進一步推演為：

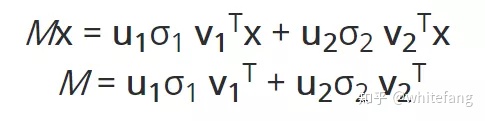
我們得到了M有關u,v,σ的表達式。將表達式轉為矩陣表達形式，即為：

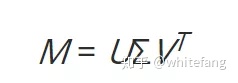
其中U中的每一列向量ui為映射后的一個單位基向量，V中的每一個列向量vj為原先被映射的單位基向量。這里的推導過于簡略，下面我們看看更為嚴格的推導。

2. 代數角度理解奇異值與奇異向量

奇異值分解在代數上表現就是A將一組正交基轉化為另一組正交基。我們來看一下具體推導。

2.1 從正交基映射推導SVD

2.1內容主要來自[5]，靖王你真帥！

假設找到了這樣一組正交基：

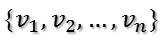
而mxn的實矩陣A將其映射為：

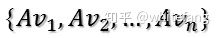
我們要使他們兩兩正交，也就是：

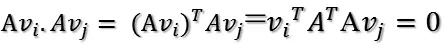
根據假設，有：

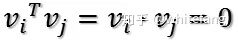
在這種情況下，如果取vi為AT的特征向量的話，那么就有：

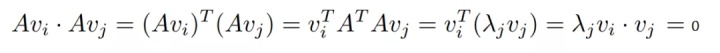
這樣我們就找到了正交基使其映射后還是正交基了。現在我們將映射后的正交基單位化。因為：

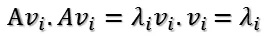
也就是：

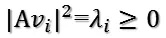
所以取單位向量為：

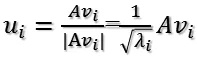
由此可得：

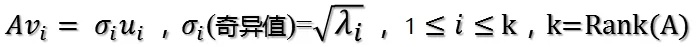
從上述公式來看，左奇異向量ui是映射后正交基的單位化形式，奇異值σi就是映射后的正交基的模的大小，而右奇異向量vi就是被映射的正交基。此處也可以看出奇異值一定非負(當然本身的定義就是這樣)。

當k < i < m時，對u1，u2，…，uk進行擴展u(k+1),…,um，使得u1，u2，…，um為m維空間中的一組正交基，即：

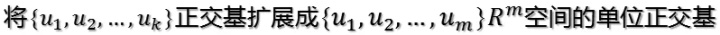
同樣的，對v1，v2，…，vk進行擴展v(k+1),…,vn（這n-k個向量存在于A的零空間中，即Ax=0的解空間的基），使得v1，v2，…，vn為n維空間中的一組正交基，即:

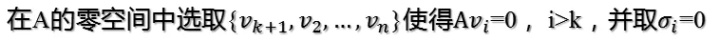
然后我們就可以得到：

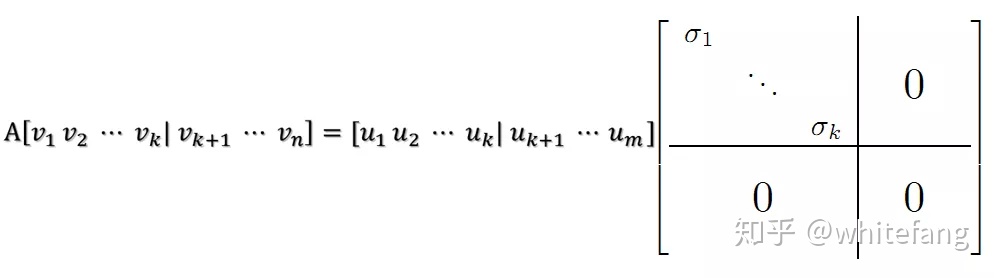
從而A的SVD分解為：

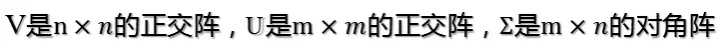
根據論文[3]的分析，任意mxn的實矩陣A=UΣVT，都可以看成一種線性轉化, 從n維空間到m維空間的轉化。n維空間和m維空間分別由V和U的列向量所形成的基向量確定。

2.2 特征值分解求解奇異值和奇異向量

2.2.1 求解過程

對任意mxn實矩陣A的奇異值分解A=

，有：

這不就是特征值分解嗎。也就是說

是

的特征向量，其對應的特征值是

，同理

是

的特征向量，其對應的特征值也是

。可以從這個角度出發求解特征值和特征向量。

實際上，對于mxn維的實矩陣A，

和

都是半正定的實對稱矩陣(特征值為非負數)，且具有相同的非零特征值。且k=rank(

)=rank(

)=rank(A)

這里的分析還可以解釋2.1中對角陣S上的i為什么最多取到k=rank(A)，假設可以取到k+1，按照本節中的推導，奇異值

是找不到對應的非零特征值的，顯然

=0。

或者說得專業些，

是實對稱矩陣，存在n階正交矩陣V，使得

相似于對角矩陣

(對角線上是

的全部特征值)。相似的矩陣有相同的特征多項式，進而有相同的特征值，當然秩更要相同了。所以r(S)=r(

)=r(

)=r(A)。即對角陣S非零奇異值的個數=

非零特征值的個數=對稱矩陣

的秩=A的秩。

2.2.2 推論

好了我們可以總結下了，對于任意實矩陣A的奇異值分解，它的右奇異向量(V的列向量)是

的特征向量，它的左奇異向量(U的列向量)是

的特征向量，而奇異值是這兩個對稱矩陣相同的非零特征值的平方根(實際上它們兩個非零特征值一模一樣)。

SVD分解只告訴我們總是存在這樣一個分解，并沒有說這個分解是唯一的。很顯然：特征值次序就可以不一樣，顯然SVD分解不唯一。但是我們常常把奇異值按照從大到小的順序排列，這樣S就可以由A唯一確定了。[7]和[8]告訴了我們SVD分解什么情況下是唯一的，感興趣可以看看。

那什么時候SVD分解和特征值分解相等呢？ [10]里面給出了一種說法：

2.3 SVD的另一種形式

實矩陣A的奇異值分解

可以表示為：

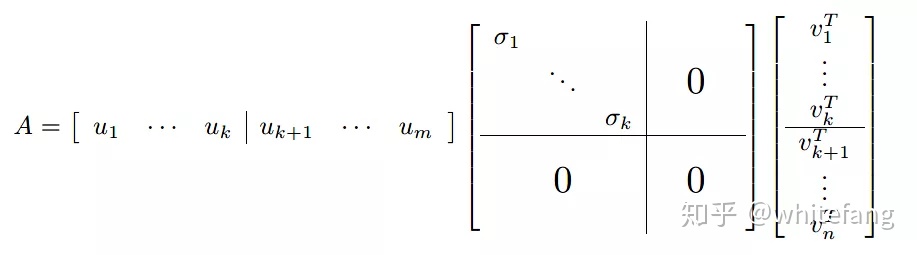
其中k=rank(A)，即矩陣A的秩。參照2.2我們知

，這些奇異值和這兩個對稱矩陣的相同特征值是一一對應關系(平方根)，顯然k<=min(m,n)。

使用矩陣的分塊乘法，得：

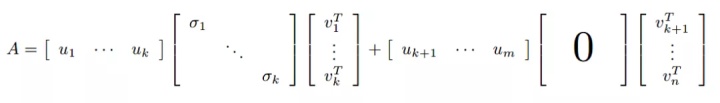
后面一項是0，所以可以化為：

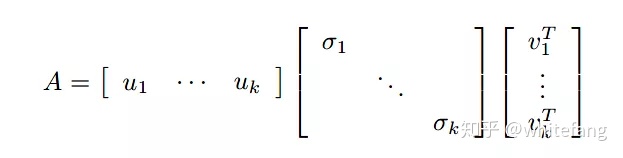
如果我們令X為mxk的矩陣,Y為kxn的矩陣：

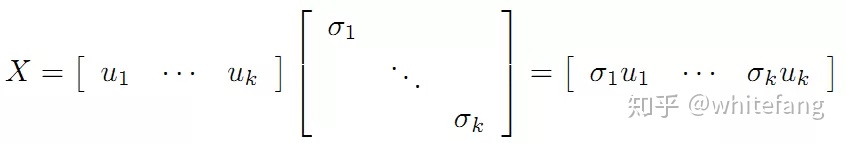
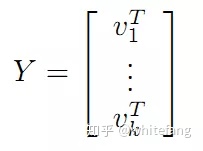
那么A可以表示為：

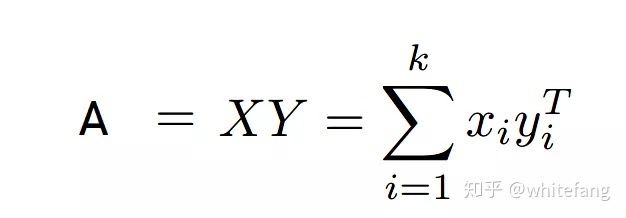
我們把它展開為向量的外積形式，這就是SVD的另一種表達形式：

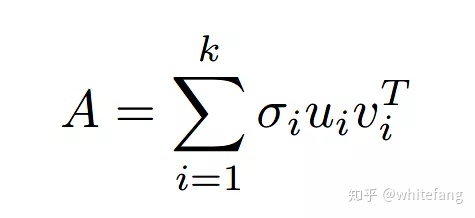
那么向量x左乘矩陣A是什么呢？我們看看：

是個標量，所以有：

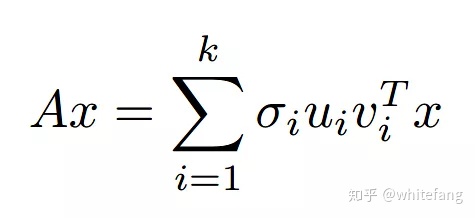
此時Ax已經表示成了

的線性組合，每一項線性系數是

和

的乘積，由矩陣乘法的本質可知，此時

可以看成x在V坐標系下

軸上的坐標。結論呼之欲出：在A的作用下，x由n維空間轉化到了m維空間中。下一章我們將從空間幾何的角度對這個轉化進行理解。

3. 幾何角度理解奇異值與奇異向量

3.1 從坐標變換理解

3.1.1 從例子到一般

我直接復制[9]中的一個例子過來，作者是西電的張劍湖大佬：

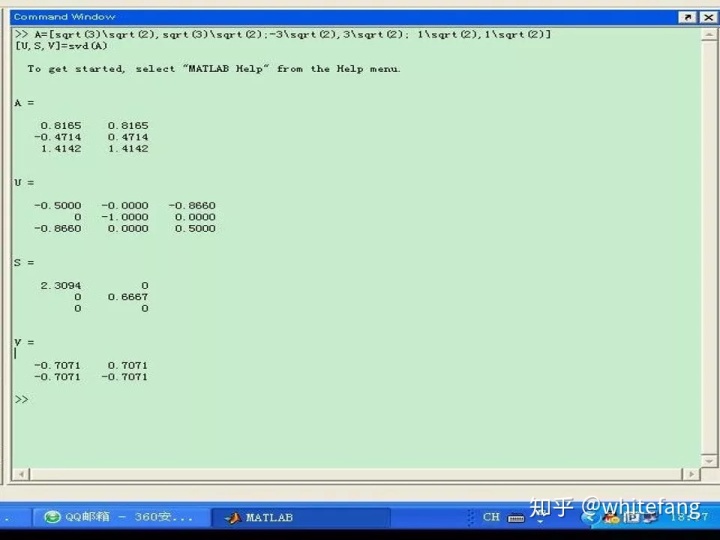
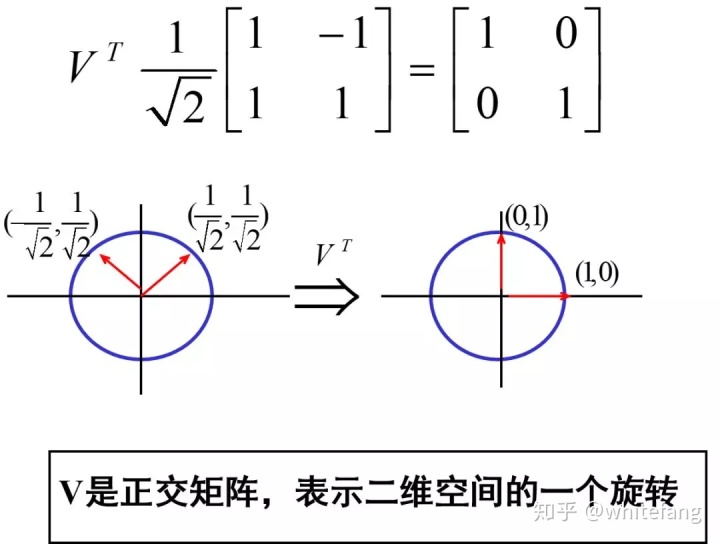
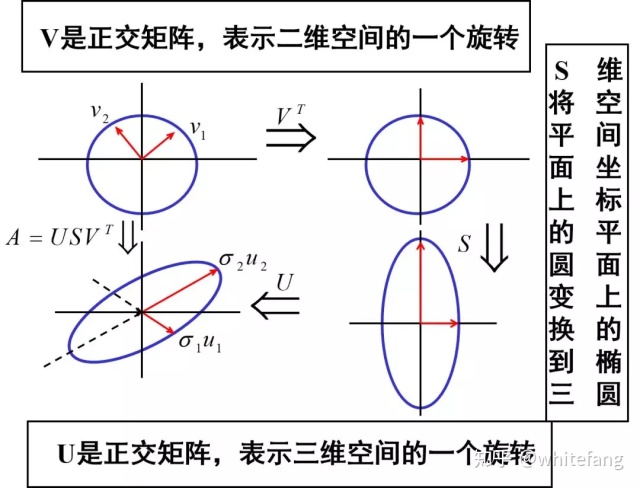
矩陣乘法的本質一文中提到過，向量左乘正交矩陣可以達到將向量旋轉的效果。我們還看了一個2階非對稱方陣的實例，它的奇異值變換就是對向量進行旋轉-縮放-旋轉的過程。當時并沒有講維度變化這個細節。

我們對更一般的形式進行分析：從奇異值分解的角度出發，

，

就是x在V每個列向量所確定的軸進行投影，是先將x映射到V坐標系中(此時x維度和V確定的空間維度相同，也可以理解為

坐標系表示的空間的維度，最后映射到

坐標系中(此時

和

坐標系維度相同，可以理解為

3.1.2 兩個問題

第一個問題是，為什么不是在

中進行長度為

的伸縮，而在

坐標系中向量的模長卻為

呢？

是這樣的，拿v1舉例吧，它太過特殊，在V坐標系中的投影坐標是(1,0,…,0)T。而Σ不僅把這個n維的進行了擴維，將n維的(1,0,…,0)T變為m維的(1,0,…,0)，同時還進行了第一維度上長度為

的伸縮成為了(

,0,…,0)。

所以，在投影到

坐標系之前，v1已經轉化成一個m空間的向量，它的模長就是

。而這個m維空間無論用哪組單位正交基來表示，只不過相當于對向量進行旋轉換了方向，向量本身的模是不變的。

第二個問題是，如果如問題1所述，那為什么投影到

坐標系中，坐標值恰好與U中的基向量是對應的？

實際上在代數上就是這樣沒有為什么。從幾何角度，我們還是在二維中進行分析吧。假設B點逆時針旋轉θ度即為A點，順時針θ度為C點。

,

坐標系和

,

坐標系就是U和

。現在對于B(

,0)，我們要向

,

坐標系中投影，由其相對關系可知，其投影坐標值其實就相當于A點在x,y坐標系中的投影坐標值，也就是(cosθ,sinθ)T*

。

發現了吧，當v1乘以對角陣S維度擴展到m時，此時它的坐標是有一個默認的坐標系的，就如下圖中的x,y坐標系。而U和

空間也如下圖中關系所示，它們使用默認坐標系中的坐標來表示自己。在默認坐標系下x和y軸向的伸縮變換在

,

中的表示，就如同

,

坐標軸向的伸縮變換在x中的表示，當然使用

,

坐標軸的基向量的表示啊。

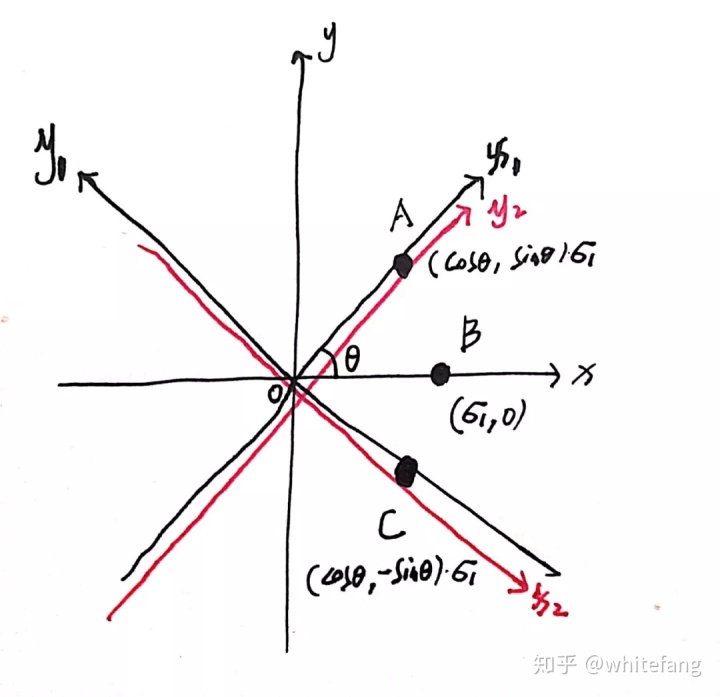
我們可以發現，對于x,y坐標系中的向量OB(

,0)，無論是逆時針轉到了坐標系

,

中變為(cosθ,sinθ)T*

，還是轉到

,

坐標系中成為(cosθ,-sinθ)T*

，它的模是不變的。這與問題一是呼應的。

3.2 形變的角度理解奇異值

在[2]中，馬同學從翻繩游戲開始，對奇異值進行了生動形象的分析，[6]中7.4節也有形變的分析，還有相關例題。感興趣的可以看一看。

4. 我覺得的最好的奇異值解讀

在知乎問題"奇異值的物理意義是什么？"下，看到一位大牛對奇異值的解讀[12]，個人認為是對奇異值的一種最好的解讀。感謝知乎用戶“老雞蛋”。

5. 特征值分解和奇異值分解區別

• 適用條件 特征值分解必須是可對角化矩陣(所以必須是方陣。n階方陣可對角化的定義是相似于一個對角矩陣，充要條件是A有n個線性無關的特征向量[11])，奇異值分解則適用于任意矩陣。
• 特征值/奇異值個數 特征值個數與矩陣的秩沒有必然關系，n階實對稱矩陣的非零特征值個數等于矩陣的秩；非零奇異值個數等于矩陣的秩。
• 幾何意義 關于幾何意義之前講的比較多，內容較多本文就不再贅述。[10]中對于奇異值分解的幾何意義給出了一個很直觀的講法：

6. 奇異值分解在PCA中的應用

在"利用SVD進行推薦（2）特征值與特征向量的直觀理解"中我們講過，對于樣本A，PCA的計算過程就是計算協方差矩陣

，然后求前k個最大特征值對應的特征向量得到投影矩陣，從而達到降維的目的。當樣本非常多的時候，計算協方差矩陣，還要進行特征值分解，這個計算量挺大的。

我們發現SVD分解

中，左奇異向量

不就是

的特征向量嗎？那我們就可以利用SVD分解來計算投影矩陣了。

[13]中Pinard大神說，有些SVD分解算法可以不用求

而直接得到A的右奇異矩陣V，也就是可以直接得到U(

的右奇異矩陣是U)，那這就很nice了。

參考文獻

[1] http://www.ams.org/publicoutreach/feature-column/fcarc-svd
[2] https://www.matongxue.com/madocs/306.html
[3] http://www-users.math.umn.edu/~lerman/math5467/svd.pdf
[4] 張紹飛. 矩陣論教程.第2版[M]. 2012.
[5]https://blog.csdn.net/zhongkejingwang/article/details/43053513
[6] Lay D , Lay. 線性代數及其應用[M]. 機械工業出版社, 2017.
[7] http://rakaposhi.eas.asu.edu/s10-cse494-mailarchive/msg00030.html
[8] https://math.stackexchange.com/questions/644327/how-unique-are-u-and-v-in-the-singular-value-decomposition
[9] https://wenku.baidu.com/view/389fabcebceb19e8b8f6ba97.html
[10] https://www.zhihu.com/question/49959130
[11] 申亞男, 張曉丹, 李為東. 線性代數.第2版[M]. 機械工業出版社, 2015.
[12] https://www.zhihu.com/question/22237507
[13] https://www.cnblogs.com/pinard/p/6251584.html

更多精彩內容請移步公眾號:推薦算法工程師