
傳統的計算快速傅里葉變換的Cooley-Tukey算法效率極高,因其主要由蝶形運算構成,所以代碼形式也非常簡單,只是需要將輸入或者輸出按照位反轉的方式重新排序。
這個重新排序的步驟并不是必須的。Clive Temperton于1991年在Self-Sorting In-Place Fast Fourier Transforms一文中給出了適用于混合基數的原地FFT算法,不需要對輸入或輸出重新排序。本文將介紹這種算法的原理并給出基數2(Radix-2)情況下的具體構造和C++實現。作為FFT算法研究成果的集大成者,FFTW已應用了這種算法。
FFT7071專欄?fourier.v.ariant.cn
預備:內存中的矩陣轉置
設x[t]為一個長度為M*N的向量,t也可表示為Ma+b。以M=5,N=3為例,x[0…14]={101, 102, 103,…, 115},如果將x視作一個5行3列的矩陣,那么a列b行的矩陣元素即是x[Ma+b]:
a= 0, 1, 2
b=0 101 106 111
b=1 102 107 112
b=2 103 108 113
b=3 104 109 114
b=4 105 110 115將這個矩陣轉置,不難發現轉置后的y[0…14]={101, 106, 111, 102,…, 110, 115}
a= 0, 1, 2, 3, 4
b=0 101 102 103 104 105
b=1 106 107 108 109 110
b=2 111 112 113 114 115y與x的關系是y[Nb+a]=x[Ma+b]。這個轉置變換也可以用一個置換矩陣P表示:y=Px。
展開:DFT變換式
記長度為
展開DFT變換得到以下表達式:
其中
利用
上式的求和等價于:
其中大括號內的求和相當于將y中的元素從地址0開始每相鄰的N個為一組總共M個長度為N的DFT。如果將y看作M行N列的矩陣,這是對每一列的變換,變換的結果依次乘以
至此,長度為MN的變換分解為了長度為M和N的兩遍短變換。如果上式中不將第一遍DFT的結果乘以
題外話:將中間結果寫到另一處存儲區x',并且以x'為輸入做第二遍變換,結果寫回x,如此往復可以解決變換無法在原地進行的問題,這即是Stockham FFT算法。但是如此一來FFT需要額外的等于x長度的內存,即需要額外O(N)的空間。因為置換群中的元素均可分解為2置換,也就是對換的乘積,置換矩陣也可做如此分解,將轉置操作變換成一系列對換,從而可在原地進行,僅需要O(1)額外空間。然而轉置只能分解為數量巨大的對換,這種操作的效率不高。這也預示著,充分利用內存中數據的對換,可以保持O(1)的額外空間需求,同時使FFT在原地進行且順序正確。
展開:DFT變換矩陣和素因子算法
運用上文得出的分解到DFT的矩陣形式:
實際變換的是y(也就是轉置的x),第一遍DFT作于相鄰的N個元素(每列),將結果逐個乘以一個旋轉因子,再變換間隔為N的每組元素(每行),這個過程對應DFT矩陣的一種分解,也就是素因子分解FFT算法的基本構造:
其中W為下標相應長度的DFT矩陣;P為x[Ma+b]轉置到y[Nb+a]的置換矩陣;I為M或N階的單位矩陣;D為M*N階對角矩陣,第bN+d行對角線上的值為exp(2πibd/(MN))。?是矩陣的Kronecker積,定義如下:
例如:
Kronecker積滿足結合律:
滿足“混合乘積”性質:
以
繼續分解
運用“混合乘積”的性質將上式拆分為矩陣積:
對于長度為
可以得到:
這種分解正是時間抽取(DIT)基數2(Radix-2)的Cooley-Tukey算法,下文中只考慮此種FFT,頻率抽取(DIF)在附錄中討論。
已知T對應Cooley-Tukey算法每次迭代在整個輸入向量上的所有蝶形運算,上式中的
2^3 2^2 2^1 2^0
[b] [b] [b] [a] = 2b+a
[a] [b] [b] [b] = 8a+b可知
2^3 2^2 2^1 2^0
[k3] [k2] [k1] [k0]
[k0] [k3] [k2] [k1] - P16
[k0] [k1] [k3] [k2] - P8
[k0] [k1] [k2] [k3] - P4很明顯T之前所有
對換:蝶形運算和對換
設DFT的長度為N,則x[t]中的t在二進制下有N位,定義
2^3 2^2 2^1 2^0
[k3] [k2] [k1] [k0]
[k0] [k2] [k1] [k3] - Q03
[k0] [k1] [k2] [k3] - Q12在N=2M或2M+1的情況下:
轉置P無法簡單地在原地計算,而Q僅包含數量較少的對換,因此可以在原地完成。目前為止以T和Q組成的DFT矩陣W分解仍然表示先重排數據再開始蝶形運算的迭代,如果將T和Q結合起來,就能省略重排數據的操作,但是這要求T和Q可交換。為了證明這一點,首先需要求出Q的表達式。
觀察
0000 0000
0001 -> 1000
0010 0010
0011 -> 1010
0100 0100
0101 -> 1100
0110 0110
0111 -> 1110
1000 -> 0001
1001 1001
1010 -> 0011
1011 1011
1100 -> 0101
1101 1101
1110 -> 0111
1111 1111可以發現
這里
在為二進制數添加前綴的操作下
00000 00000 10000 10000
00001 -> 01000 10001 -> 11000
00010 00010 10010 10010
00011 -> 01010 10011 -> 11010
00100 00100 10100 10100
00101 -> 01100 10101 -> 11100
00110 00110 10110 10110
00111 -> 01110 10111 -> 11110
01000 -> 00001 11000 -> 10001
01001 01001 11001 11001
01010 -> 00011 11010 -> 10011
01011 01011 11011 11011
01100 -> 00101 11100 -> 10101
01101 01101 11101 11101
01110 -> 00111 11110 -> 10111
01111 01111 11111 11111因此對于N位二進制數:
為二進制數添加后綴的操作使
設
因此對于所有的
已知一次蝶形運算的迭代
令
可見

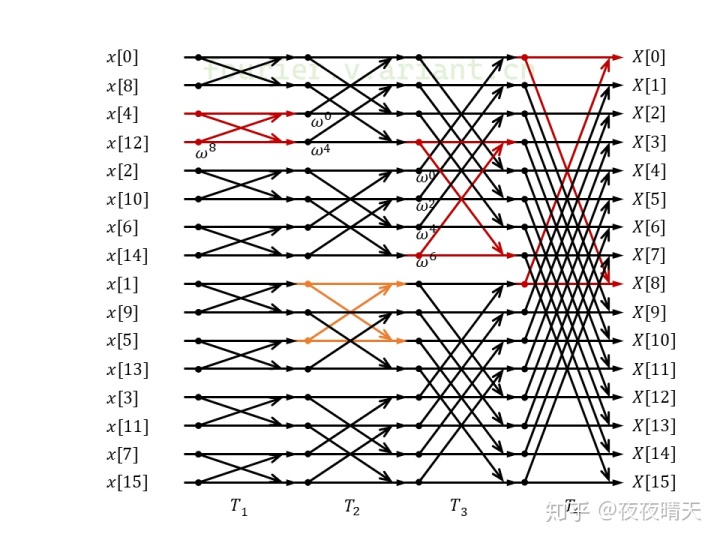
下圖中畫出來N=16的基數2變換,輸入和輸出的順序均是正確的;圖中用顏色標出了某些蝶形運算,使蝶形運算的配對更清晰。注意其中成對蝶形運算的4個輸入輸出均在原地,并且與傳統Cooley-Tukey算法相比沒有計算量的差別。

下圖是作為對比的傳統Cooley-Tukey算法。
附錄:本文算法的C++實現
/* copyright 2020, github.com/zhxxch, all rights reserved. */
#include <complex>
#include <iterator>
#include <cmath>
#include <cassert>
#include <cstddef>
template<typename iter_t>
#if __cplusplus > 201703L
requires std::random_access_iterator<iter_t>
#endifinline void fft_in_place(iter_t arr_begin,iter_t arr_end, const bool is_inverse) {using cplx_t = typename std::iterator_traits<iter_t>::value_type;using real_t = typename cplx_t::value_type;const size_t length= std::distance(arr_begin, arr_end);assert("requires length = pow(2,n)"&& (length & (length - 1)) == 0);constexpr real_t pi= 3.141592653589793238462643383;size_t sub_ft_size = 1;size_t num_sub_ft = length / sub_ft_size;size_t num_sub_ft_pair = num_sub_ft / 2;for(; sub_ft_size < num_sub_ft_pair;sub_ft_size *= 2, num_sub_ft /= 2,num_sub_ft_pair /= 2) {for(size_t coupled_group_pos = 0;coupled_group_pos < length;coupled_group_pos += 2 * num_sub_ft_pair) {for(size_t sub_ft_pos = coupled_group_pos;sub_ft_pos< coupled_group_pos + num_sub_ft_pair;sub_ft_pos += 2 * sub_ft_size) {for(size_t i = sub_ft_pos, nth_pow = 0;i < sub_ft_pos + sub_ft_size;i++, nth_pow += num_sub_ft_pair) {const cplx_t W = exp((is_inverse ? 1. : -1.)* cplx_t(0, 2 * nth_pow * pi)/ (real_t)length);const cplx_t parit00= arr_begin[i];const cplx_t parit01= arr_begin[num_sub_ft_pair+ i]* W;const cplx_t parit10= arr_begin[i + sub_ft_size];const cplx_t parit11= arr_begin[num_sub_ft_pair + i+ sub_ft_size]* W;arr_begin[i] = parit00 + parit01;arr_begin[i + sub_ft_size]= parit00 - parit01;arr_begin[num_sub_ft_pair + i]= parit10 + parit11;arr_begin[num_sub_ft_pair + i+ sub_ft_size]= parit10 - parit11;}}}}for(; sub_ft_size < length; sub_ft_size *= 2,num_sub_ft /= 2, num_sub_ft_pair /= 2) {for(size_t sub_ft_pos = 0; sub_ft_pos < length;sub_ft_pos += 2 * sub_ft_size) {for(size_t i = sub_ft_pos, nth_pow = 0;i < sub_ft_pos + sub_ft_size;i++, nth_pow += num_sub_ft_pair) {const cplx_t parit1= arr_begin[i + sub_ft_size]* exp((is_inverse ? 1. : -1.)* cplx_t(0, 2 * nth_pow * pi)/ (real_t)length);const cplx_t parit0 = arr_begin[i];arr_begin[i] = parit0 + parit1;arr_begin[i + sub_ft_size]= parit0 - parit1;}}}
}
使用方法-FFT
fft_in_place(arr.begin(), arr.end(), 0);
使用方法-IFFT
fft_in_place(arr.begin(), arr.end(), 1);
arr的長度必須是2的冪。
附錄:時間抽取與頻率抽取
以
換為使用Q表達的形式則為:
因此Q作用于蝶形運算的輸出。
)











:開啟net.tcp端口)


![Sgen.exe: Speed up XmlSerializer's Startup Performance [.NET 2.0, XML Serialization]](http://pic.xiahunao.cn/Sgen.exe: Speed up XmlSerializer's Startup Performance [.NET 2.0, XML Serialization])



