快速排序 C++

本文圖示借鑒自清華大學鄧俊輝老師數據結構課程。

快速排序的思想

快速排序是分治思想的典型應用。該排序算法可以原地實現，即空間復雜度為 $O(1)$，而時間復雜度為 $O(nlogn)$ 。

算法將待排序的序列 $S$ 分為兩個子序列 $S_L$ 和 $S_R$ ，隨著這種子序列的劃分，可以保證問題的規模在不斷縮小，即有：
$$max(|S_L|,|S_R|)<n$$
并要求左側子序列 $S_L$ 中的最大值不大于右側子序列 $S_R$ 中的最小值，即有：
$$max(S_L)\le min(S_R)$$
這樣在遞歸地再對子序列進行劃分之后，原序列自然有序。遞歸的終止條件為劃分子序列的平凡情況，即子序列的規模為1。

我們將劃分兩個子序列的點稱為 pivot（軸點） ，在軸點左側的元素，均不比它更大；在軸點右側的元素，均不比它更小。軸點的位置，即為該元素在最終排序完成的序列中的位置。

即將原序列按如下劃分：
$$[l,r]=[l,pivot)+pivot+(pivot,r]$$
但是對于待排序的序列，我們并不知道誰是軸點，甚至，有可能原序列中所有元素都不是軸點，比如將一個已排序的序列循環右移一位，則此時所有元素都不在自己的排序位置上，都不是軸點。

好在我們可以通過對待排序的序列的元素進行移動交換，從而使得某個元素成為軸點，在遞歸之后，所有元素都成為軸點，這時所有元素都位于自己的排序位置上，整個排序算法完成。

可以看到，整個算法的框架是遞歸地選取軸點并劃分子序列，究竟怎樣劃分，怎樣劃分效率更高，是快排算法的關鍵之處。

算法框架

我們先給出整個快排算法的遞歸框架，其中關鍵的 partition 劃分函數我們會在后面詳細介紹，整體框架是一個遞歸函數：

void quickSort(vector<int>& vec, int l, int r) {if (l<r) {int pivot = partition(vec, l, r);quickSort(vec, l, pivot-1);quickSort(vec, pivot+1, r);}
}

當 l 不小于 r 時，即 l 已經等于 r，此時即為遞歸退出的平凡情況：子序列只有一個元素。在此之前，我們都需要不斷地執行 if 語句中的內容：得到傳入序列的一個軸點，并分別遞歸地處理該軸點兩側的子序列。

最終當傳入的子序列規模為1是，即 l<r 的判斷條件不成立，達到返回條件，整個遞歸過程開始返回。

partition

版本1

接下來我們來介紹最為關鍵的 partition 函數。

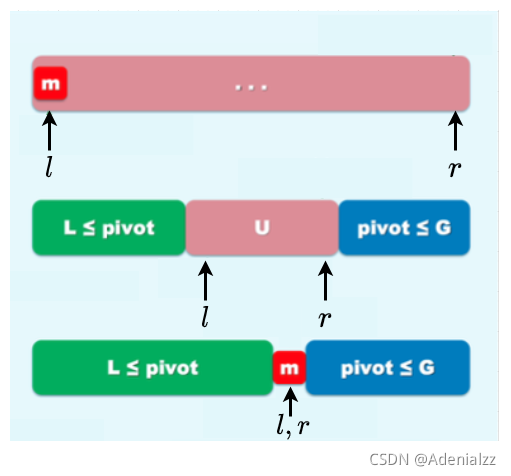
我們先任選一個元素作為軸點的 “培養對象” 并備份，在我們劃分完畢之后，該元素可以 “名正言順” 地位于自己應該處于的最終排序位置，不妨就取序列的最左端元素。

然后將兩個指針分別放在整個序列的左右兩端，分別向中間靠攏。

我們將

• 未確定區域稱為 $U$ （圖中粉色部分），初始為全集
• 確定大于軸點的部分稱為 $G$ （圖中藍色部分），初始為空集
• 確定小于軸點的部分稱為 $L$ （圖中綠色部分），初始為空集

交替地將左右兩端的指針向中間移動，分別檢查移動時當前元素與軸點 pivot 的大小關系，若小于軸點，則歸入 $L$；若大于軸點，則歸入 $R$ 。

當左右兩指針相等時，該位置即為我們的 “培養對象” 軸點應該處于的排序位置，將備份的軸點放入該位置即可。最后同樣返回軸點位置。

整個過程中，左右指針所指的位置交替空閑。所謂空閑即是指其中元素可以被覆蓋。一開始時，我們將 ”培養對象“ 備份，故其位置是 “空閑” 的，在隨后的交還過程中，左右指針總有一個所指的位置是空閑的。

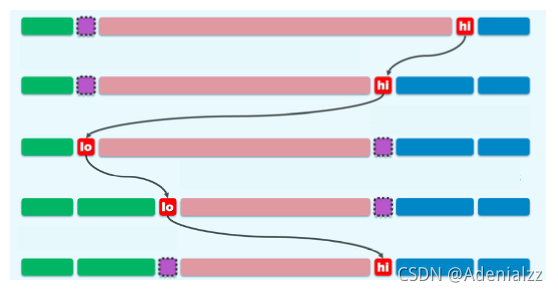
可以參考上圖，圖中紫色部分即為 “空閑” 的。紅色的 lo、hi 分別對應我們描述中的左右指針。

代碼實現如下：

int partition(vector<int>& vec, int l, int r) {int pivot = vec[l];while(l < r) {while (l<r && pivot<=vec[r]) r--;swap(vec[r], vec[l]);while (l<r && pivot>=vec[l]) l++;swap(vec[r], vec[l]);}vec[l] = pivot;return l;
}

版本2

對于 partition 函數，還有一種實現的方式，可以稱為 LGU 的方式，在這種方式中，L 仍舊排在原序列的最左端，而中間是 G ，最右端是 U。

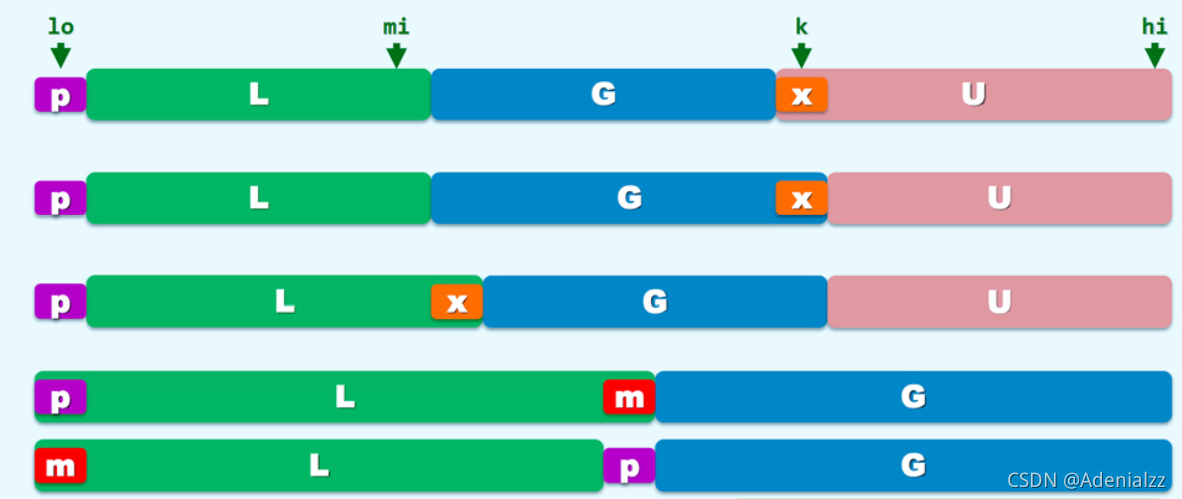
同樣可以選取最左端的元素作為 pivot 。

然后一根指針從序列的最左端遍歷到最右端，分別判斷每個當前元素與 pivot 的關系，并分別劃分到 L 或 G 中。

如果是劃分到 G 中，直接將 k++ 即可；而如果是劃分到 L 中，則需要將 G 滾動后移一個元素，并將當前元素交換到 L 的末尾。

代碼實現如下：

int partition(vector<int>& vec, int l, int r) {int m = l, pivot = vec[l];for (int k=l+1; k<=r; k++) {if (pivot > vec[k])swap(vec[++m], vec[k]);}swap(vec[l], vec[m]);return m;
}

這里中間判斷中的 if 分支是判斷當前元素小于軸點 pivot ，需要將當前元素加入到 L 中，將當前元素 vec[k] 與 L 的最后一個元素 vec[++m] 互換，然后k++；而它對應的 else 分支，即當前元素小于軸點 pivot，需要將當前元素加入到 G 中，此時只需將 k++。兩個分支都需要 k++，直接放在循環變量的更新中。

最后同樣返回軸點位置。