高并發內存池性能瓶頸分析與基數樹優化(9)

文章目錄

前言
一、性能瓶頸分析
- 操作步驟及其環境配置
- 分析性能瓶頸
二、基數樹優化
- 單層基數樹
- 二層基數樹
- 三層基數樹
三、使用基數樹來優化代碼
總結

前言

??到了最后一篇嘍，嘻嘻！
??終于是要告一段落了，接下來我們將學什么呢，再說吧，可能得把Linux的一些內容給補完

一、性能瓶頸分析

操作步驟及其環境配置

??我們的代碼此時與 malloc 之間還是有差距的，所以現在我們來分析一下我們的代碼

??這里就要借助 VS 的一些神奇妙妙功能了，首先先確保在 Debug 環境下運行，依次點擊“調試→性能探查器”進行性能分析

在這里插入圖片描述
??同時我們屏蔽一下 malloc / free 的 BenchMark 函數，而是就對我們自己的內存池進行分析

int main()
{size_t n = 10000;cout << "==========================================================" << endl;BenchmarkConcurrentMalloc(n, 4, 10);cout << endl << endl;//BenchmarkMalloc(n, 4, 10);cout << "==========================================================" << endl;return 0;
}

??接下來我們點擊勾選“檢測”，再點擊“開始”進行
在這里插入圖片描述

??接著會彈出這個頁面，說明此時此刻你沒配置，當然了，我一開始也沒有

在這里插入圖片描述

??那具體要怎么配置呢？直接就來個講解吧！先右鍵項目名稱，然后再點擊屬性

在這里插入圖片描述

??然后再依次 點擊配置屬性 -> 點擊鏈接器 -> 點擊高級 -> 將配置文件設置為是(/PROFILE)

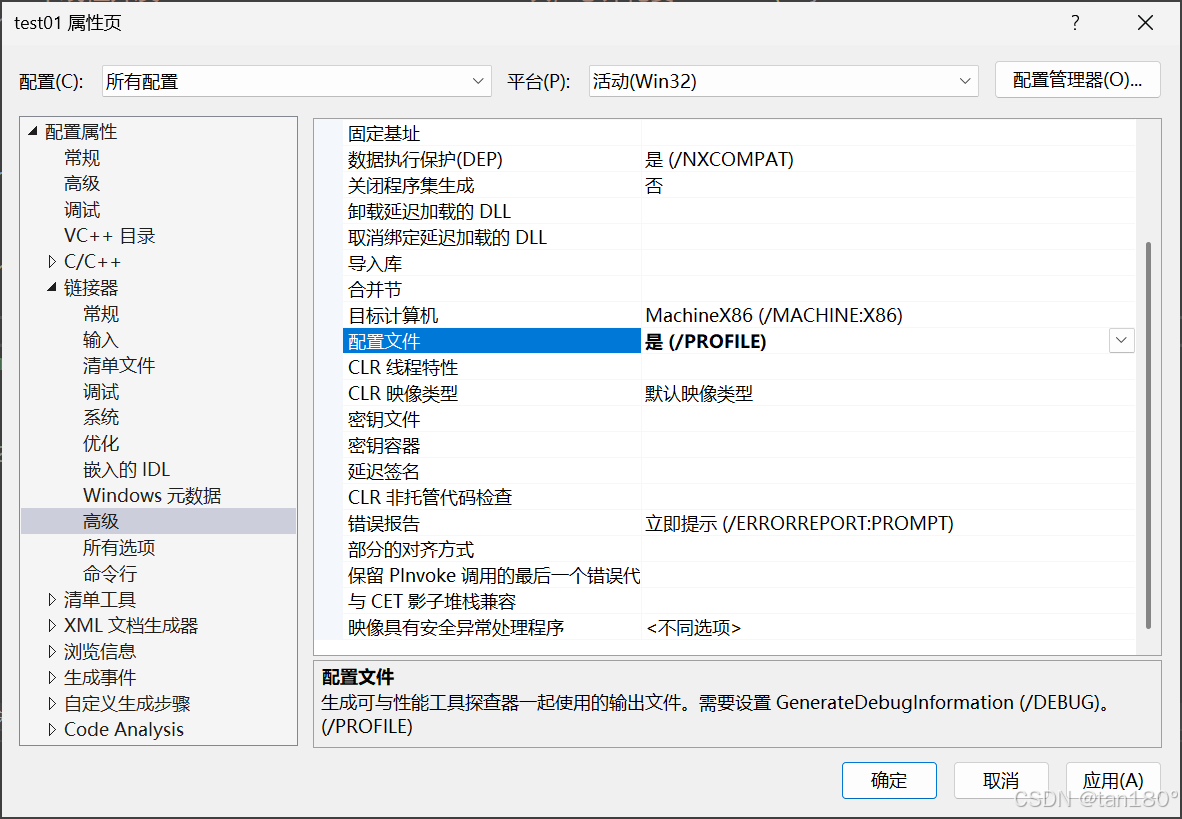
在這里插入圖片描述
????好了這下你就配置好了，那么我們接下來繼續啟動性能分析器，看看到底怎么個說法

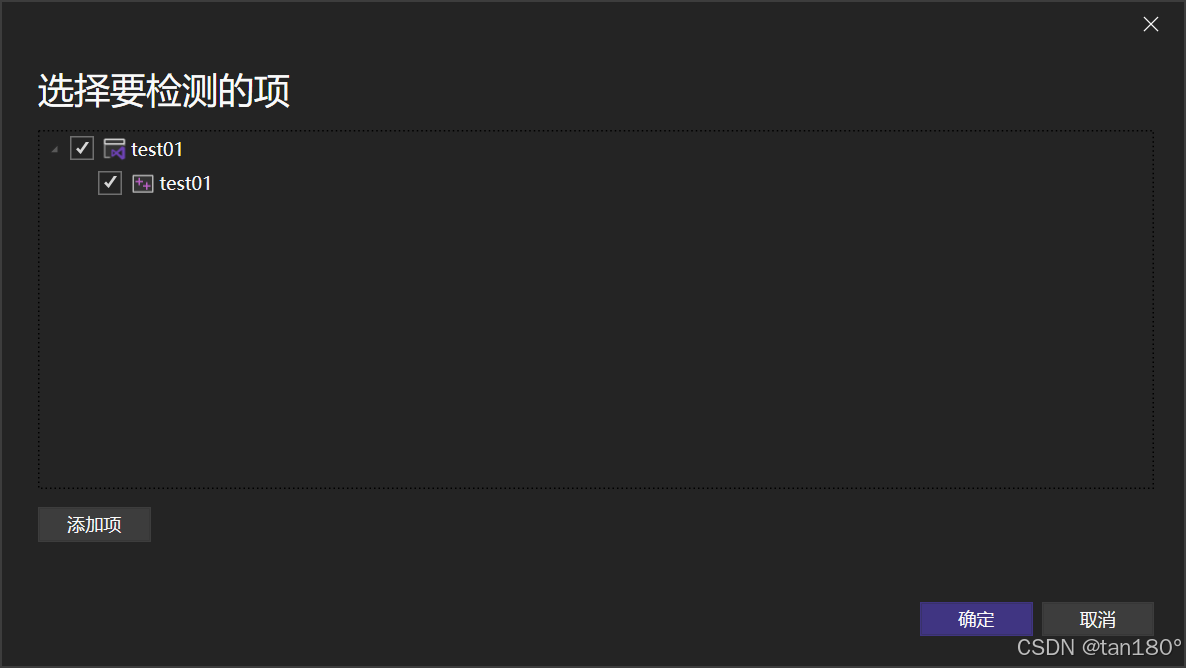
在這里插入圖片描述
????接下來就靜靜等待結果就好了

分析性能瓶頸

????通過分析結果可以看到，ConcurrentAlloc 和 ConcurrentFree 這兩個函數占用了接近60%的時間
在這里插入圖片描述

????接著將視圖修改為調用方/被調用方，這樣看起來更加直觀

在這里插入圖片描述
????點擊占用時間最多的 Allocate ，再點擊占用時間最多的 FetchFromCentralCache ，再點擊占用時間最多的 FetchRangeObj ，再點擊占用時間最多的 GetOneSpan ，再點擊進去就是 lock函數占用最多時間了，事實上 ConcurrentAlloc 也同樣如此，就是因為鎖競爭導致了浪費那么多的時間

????針對此瓶頸，我們想到了使用基數樹進行性能優化

二、基數樹優化

??基數樹實際上就是一個分層的哈希表，根據所分層數不同可分為單層基數樹、二層基數樹、三層基數樹等。

??或者我們不如先來想想為什么要加鎖，無非就是因為STL底層不保證線程安全，因為 unordered_map的底層數據結構是紅黑樹，在訪問映射關系的時候如果另一個線程進行添加映射的時候，可能由于插入或者旋轉導致讀取線程發生錯誤，而基數樹就可以完全避免這個問題，至于N層只是說根據不同環境下的不同選擇

單層基數樹

????因為我是在 32位環境下寫的，所以我將選擇這個基數樹，當然原理都是一樣的，如果你是64位環境下，那我還是建議你用三層基數樹吧

????單層基數樹實際采用的就是直接定址法，每一個頁號對應 span 的地址就存儲數組中在以該頁號為下標的位置。

在這里插入圖片描述
????最壞的情況下我們需要建立所有頁號與其 span 之間的映射關系，因此這個數組中元素個數應該與頁號的數目相同，數組中每個位置存儲的就是對應 span 的指針

//單層基數樹
template <int BITS>
class TCMalloc_PageMap1
{
public:typedef uintptr_t Number;explicit TCMalloc_PageMap1(){size_t size = sizeof(void*) << BITS; //需要開辟數組的大小size_t alignSize = SizeClass::_RoundUp(size, 1 << PAGE_SHIFT); //按頁對齊后的大小array_ = (void**)SystemAlloc(alignSize >> PAGE_SHIFT); //向堆申請空間memset(array_, 0, size); //對申請到的內存進行清理}void* get(Number k) const{if ((k >> BITS) > 0) //k的范圍不在[0, 2^BITS-1]{return NULL;}return array_[k]; //返回該頁號對應的span}void set(Number k, void* v){assert((k >> BITS) == 0); //k的范圍必須在[0, 2^BITS-1]array_[k] = v; //建立映射}
private:void** array_; //存儲映射關系的數組static const int LENGTH = 1 << BITS; //頁的數目
};

????當我們需要建立映射時就調用set函數，需要讀取映射關系時，就調用get函數

????比如32位平臺下，以一頁大小為8K為例，此時頁的數目就是2 ^ 32 ÷ 2 ^ 13 = 2 ^ 19 ，因此存儲頁號最多需要19個比特位，此時傳入非類型模板參數的值就是32 ? 13 = 19。由于32位平臺下指針的大小是4字節，因此該數組的大小就是2 ^ 19 × 4 = 2 ^ 21 = 2 M ，內存消耗不大，是可行的。但如果是在64位平臺下，此時該數組的大小是2 ^ 51 × 8 = 2 ^ 54 = 2 ^ 24 G ，這顯然是不可行的，實際上對于64位的平臺，我們需要使用三層基數樹

????其實又是時間換空間的思想，這真是一個經久不衰的結論

下面是DS大人給出的結合比喻的解析
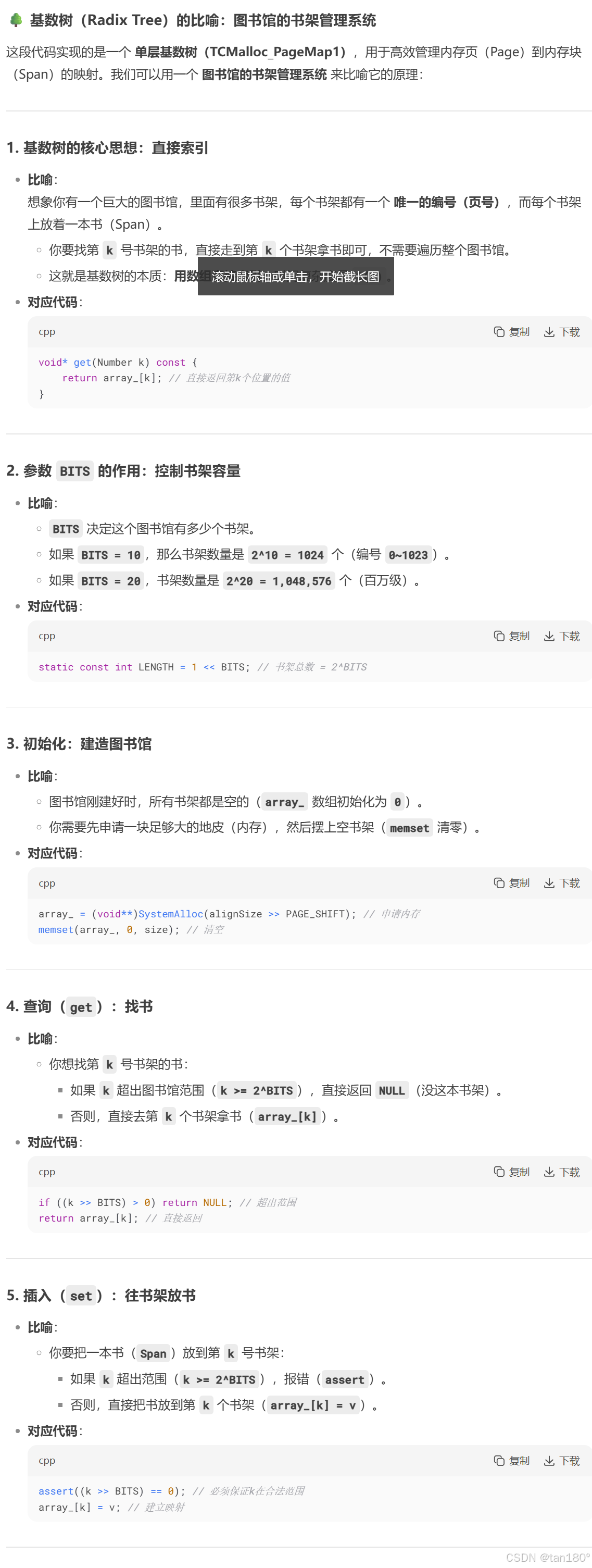
在這里插入圖片描述

二層基數樹

????這里還是以 32位平臺下，一頁的大小為 8K 為例來說明，此時存儲頁號最多需要 19個比特位。而二層基數樹實際上就是把這 19個比特位分為兩次進行映射。

????比如用前5個比特位在基數樹的第一層進行映射，映射后得到對應的第二層，然后用剩下的比特位在基數樹的第二層進行映射，映射后最終得到該頁號對應的span指針。

????在二層基數樹中，第一層的數組占用 2 ^ 5 × 4 = 2 ^ 7 Byte 空間，第二層的數組最多占用 2 ^ 5 × 2 ^ 14 × 4 = 2 ^ 21 = 2 M 。二層基數樹相比一層基數樹的好處就是，一層基數樹必須一開始就把 2 M 的數組開辟出來，而二層基數樹一開始時只需將第一層的數組開辟出來，當需要進行某一頁號映射時再開辟對應的第二層的數組就行了

//二層基數樹
template <int BITS>
class TCMalloc_PageMap2
{
private:static const int ROOT_BITS = 5;                //第一層對應頁號的前5個比特位static const int ROOT_LENGTH = 1 << ROOT_BITS; //第一層存儲元素的個數static const int LEAF_BITS = BITS - ROOT_BITS; //第二層對應頁號的其余比特位static const int LEAF_LENGTH = 1 << LEAF_BITS; //第二層存儲元素的個數//第一層數組中存儲的元素類型struct Leaf{void* values[LEAF_LENGTH];};Leaf* root_[ROOT_LENGTH]; //第一層數組
public:typedef uintptr_t Number;explicit TCMalloc_PageMap2(){memset(root_, 0, sizeof(root_)); //將第一層的空間進行清理PreallocateMoreMemory(); //直接將第二層全部開辟}void* get(Number k) const{const Number i1 = k >> LEAF_BITS;        //第一層對應的下標const Number i2 = k & (LEAF_LENGTH - 1); //第二層對應的下標if ((k >> BITS) > 0 || root_[i1] == NULL) //頁號值不在范圍或沒有建立過映射{return NULL;}return root_[i1]->values[i2]; //返回該頁號對應span的指針}void set(Number k, void* v){const Number i1 = k >> LEAF_BITS;        //第一層對應的下標const Number i2 = k & (LEAF_LENGTH - 1); //第二層對應的下標assert(i1 < ROOT_LENGTH);root_[i1]->values[i2] = v; //建立該頁號與對應span的映射}//確保映射[start,start_n-1]頁號的空間是開辟好了的bool Ensure(Number start, size_t n){for (Number key = start; key <= start + n - 1;){const Number i1 = key >> LEAF_BITS;if (i1 >= ROOT_LENGTH) //頁號超出范圍return false;if (root_[i1] == NULL) //第一層i1下標指向的空間未開辟{//開辟對應空間static ObjectPool<Leaf> leafPool;Leaf* leaf = (Leaf*)leafPool.New();memset(leaf, 0, sizeof(*leaf));root_[i1] = leaf;}key = ((key >> LEAF_BITS) + 1) << LEAF_BITS; //繼續后續檢查}return true;}void PreallocateMoreMemory(){Ensure(0, 1 << BITS); //將第二層的空間全部開辟好}
};

????下面又是DS大人給出的解釋

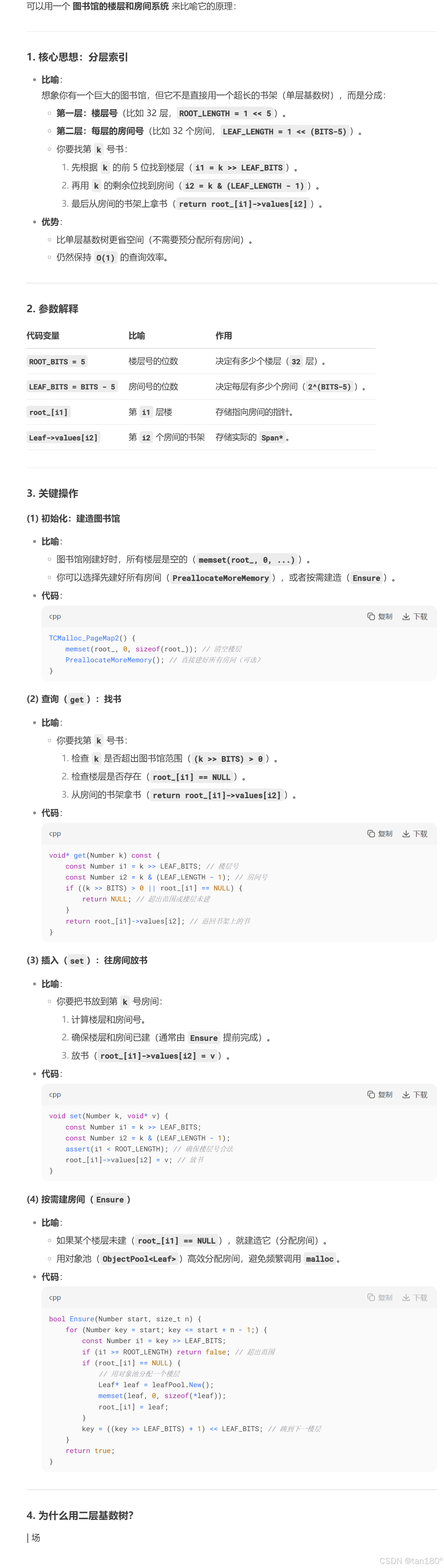
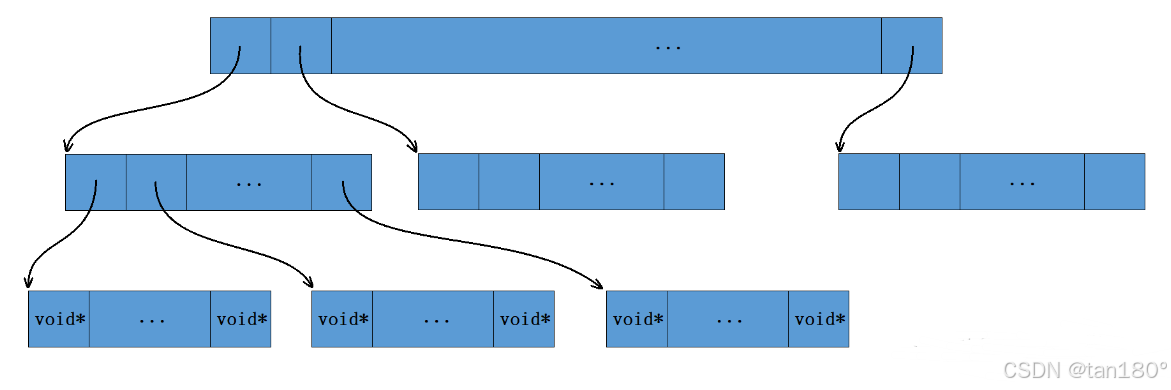
在這里插入圖片描述

三層基數樹

????原理圖如下，其實還是很好看的
在這里插入圖片描述

//三層基數樹
template <int BITS>
class TCMalloc_PageMap3
{
private:static const int INTERIOR_BITS = (BITS + 2) / 3;       //第一、二層對應頁號的比特位個數static const int INTERIOR_LENGTH = 1 << INTERIOR_BITS; //第一、二層存儲元素的個數static const int LEAF_BITS = BITS - 2 * INTERIOR_BITS; //第三層對應頁號的比特位個數static const int LEAF_LENGTH = 1 << LEAF_BITS;         //第三層存儲元素的個數struct Node{Node* ptrs[INTERIOR_LENGTH];};struct Leaf{void* values[LEAF_LENGTH];};Node* NewNode(){static ObjectPool<Node> nodePool;Node* result = nodePool.New();if (result != NULL){memset(result, 0, sizeof(*result));}return result;}Node* root_;
public:typedef uintptr_t Number;explicit TCMalloc_PageMap3(){root_ = NewNode();}void* get(Number k) const{const Number i1 = k >> (LEAF_BITS + INTERIOR_BITS);         //第一層對應的下標const Number i2 = (k >> LEAF_BITS) & (INTERIOR_LENGTH - 1); //第二層對應的下標const Number i3 = k & (LEAF_LENGTH - 1);                    //第三層對應的下標//頁號超出范圍，或映射該頁號的空間未開辟if ((k >> BITS) > 0 || root_->ptrs[i1] == NULL || root_->ptrs[i1]->ptrs[i2] == NULL){return NULL;}return reinterpret_cast<Leaf*>(root_->ptrs[i1]->ptrs[i2])->values[i3]; //返回該頁號對應span的指針}void set(Number k, void* v){assert(k >> BITS == 0);const Number i1 = k >> (LEAF_BITS + INTERIOR_BITS);         //第一層對應的下標const Number i2 = (k >> LEAF_BITS) & (INTERIOR_LENGTH - 1); //第二層對應的下標const Number i3 = k & (LEAF_LENGTH - 1);                    //第三層對應的下標Ensure(k, 1); //確保映射第k頁頁號的空間是開辟好了的reinterpret_cast<Leaf*>(root_->ptrs[i1]->ptrs[i2])->values[i3] = v; //建立該頁號與對應span的映射}//確保映射[start,start+n-1]頁號的空間是開辟好了的bool Ensure(Number start, size_t n){for (Number key = start; key <= start + n - 1;){const Number i1 = key >> (LEAF_BITS + INTERIOR_BITS);         //第一層對應的下標const Number i2 = (key >> LEAF_BITS) & (INTERIOR_LENGTH - 1); //第二層對應的下標if (i1 >= INTERIOR_LENGTH || i2 >= INTERIOR_LENGTH) //下標值超出范圍return false;if (root_->ptrs[i1] == NULL) //第一層i1下標指向的空間未開辟{//開辟對應空間Node* n = NewNode();if (n == NULL) return false;root_->ptrs[i1] = n;}if (root_->ptrs[i1]->ptrs[i2] == NULL) //第二層i2下標指向的空間未開辟{//開辟對應空間static ObjectPool<Leaf> leafPool;Leaf* leaf = leafPool.New();if (leaf == NULL) return false;memset(leaf, 0, sizeof(*leaf));root_->ptrs[i1]->ptrs[i2] = reinterpret_cast<Node*>(leaf);}key = ((key >> LEAF_BITS) + 1) << LEAF_BITS; //繼續后續檢查}return true;}void PreallocateMoreMemory(){}
};

????當然要注意的是此時只有當要建立某一頁號的映射關系時，再開辟對應的數組空間，而沒有建立映射的頁號就可以不用開辟其對應的數組空間，此時就能在一定程度上節省內存空間

三、使用基數樹來優化代碼

????此時將 PageCache類當中的 unorder_map 用基數樹進行替換即可，由于當前是 32位平臺，因此這里隨便用幾層基數樹都可以

// 單例模式
class PageCache
{
public://...
private://std::unordered_map<PAGE_ID, Span*> _idSpanMap;TCMalloc_PageMap1<32 - PAGE_SHIFT> _idSpanMap;
};

????當我們需要建立頁號與span的映射時，就調用基數樹當中的set函數。

_idSpanMap.set(span->_pageId, span);

????而當我們需要讀取某一頁號對應的span時，就調用基數樹當中的get函數

Span* ret = (Span*)_idSpanMap.get(id);

????并且現在 PageCache類向外提供的，用于讀取映射關系的 MapObjectToSpan函數內部就不需要加鎖了（因為基數樹空間固定，支持并發訪問）

//獲取從對象到span的映射
Span* PageCache::MapObjectToSpan(void* obj)
{PAGE_ID id = (PAGE_ID)obj >> PAGE_SHIFT; //頁號Span* ret = (Span*)_idSpanMap.get(id);assert(ret != nullptr);return ret;
}

????最后看看效果吧，下面是添加了基數樹優化后的對比，依次是固定內存大小、不固定內存大小

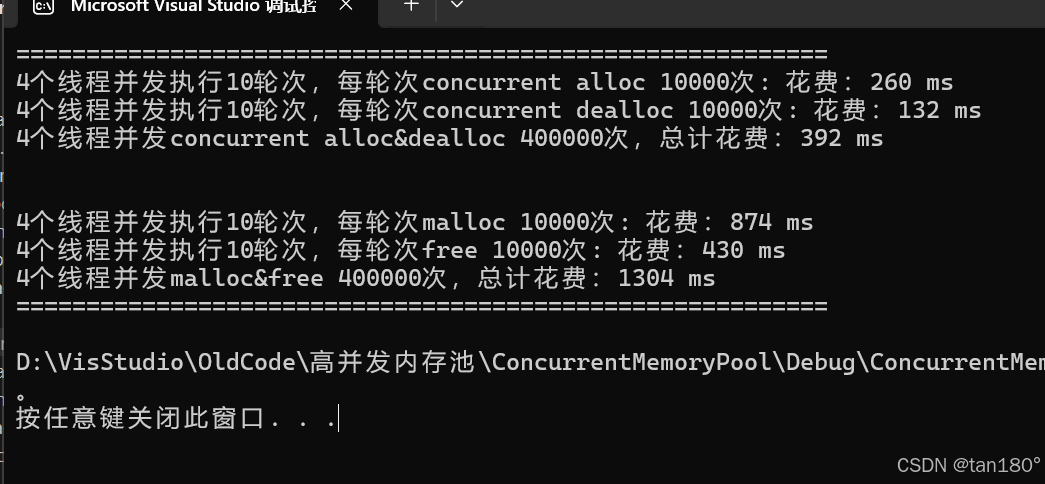
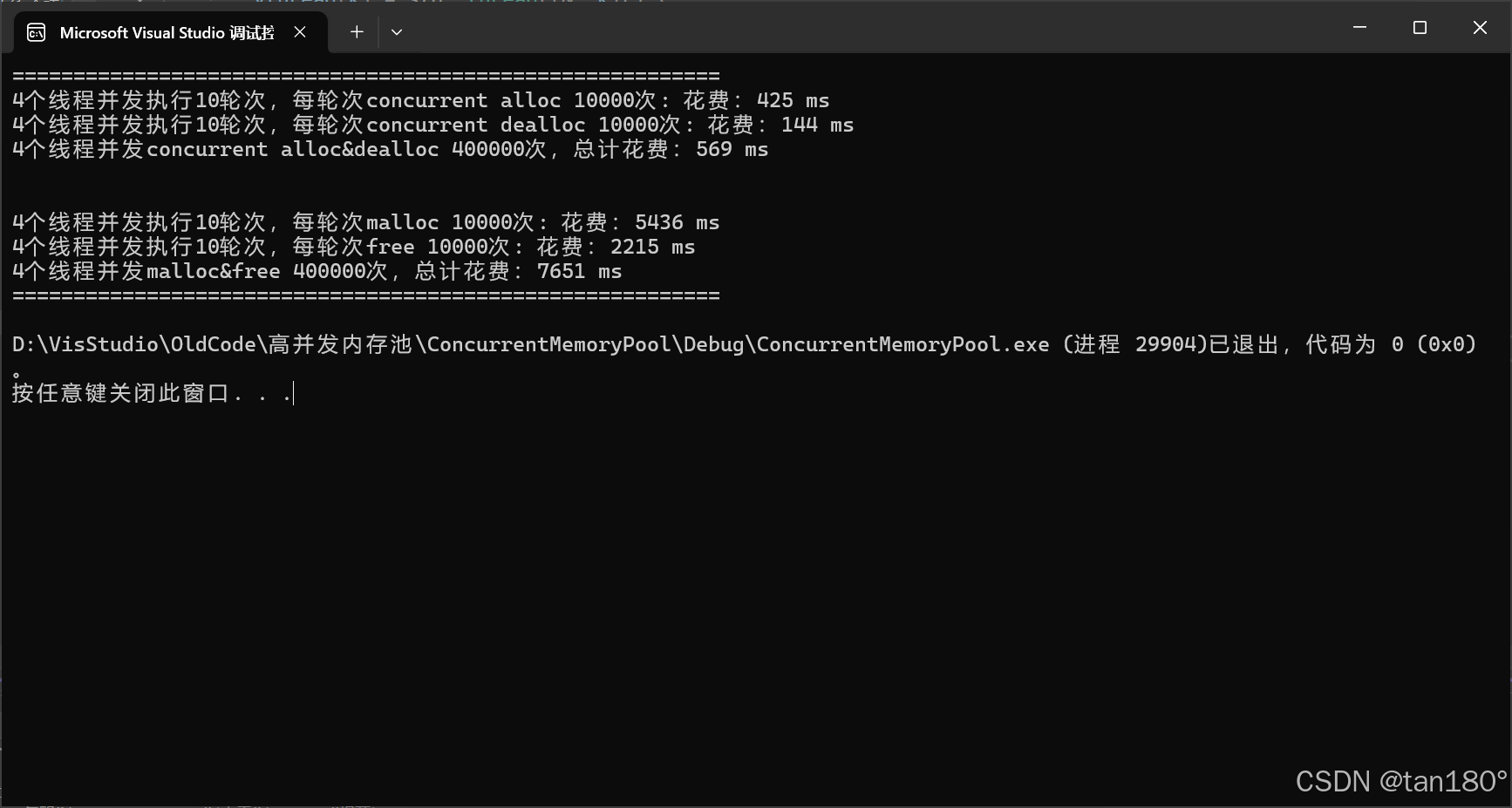
在這里插入圖片描述

????可以看到在不固定內存大小的前提下，由于 central cache 的桶鎖機制，對比差距更大了

總結

??代碼的世界里，沒有“完美”，只有“不斷迭代”，這個內存池是我的第一個項目，也是第一個孩子，過去學到的“鎖優化”“內存對齊”“數據結構”不再是抽象概念，而是解決實際問題的工具，C++本身就與性能優化及其相關，通過這個項目也是領悟到了鎖的魅力，真切感受到了工程能力的成長

??下一步可以怎么繼續加深學習呢，或許可以嘗試將內存池嵌入實際應用（如HTTP服務器）？不過那是之后的事了呢，但是我現在需要休息一下~