許多教育統計的初學者都表示這幾個分布感到學起來非常吃力,結合最近上課的體會以及答疑的情況,覺得很有必要在這里簡單地對這部分內容進行澄清和梳理,以助理解。
首先,“為什么要學習這幾個分布”可能是許多人糾結的問題,明明已經在電腦中裝了SPSS軟件了,那么復雜而繁瑣的公式不應該直接內置在軟件之中就可以了嗎?為什么還要花費功夫去學習它們呢?我只能說,在你對這部分內容不甚了解的情況下,你很難意識到其重要性。這些分布都各有所長,也就因為自然界和社會系統中這些分布存在的廣泛性,使得教育統計領域許多習以為常的假設背后都有充分的根據,例如為什么心理能力測量數據的相關性可以選用皮爾遜(Pearson)系數、為什么樣本的數量要在30個以上、為什么只有達到“顯著性水平”,才能說不同的變量之間存在統計意義上的差異等……諸如這樣的例子背后,都與數據的這些分布特征有關,正是由于知道如果從某個總體中抽取一定的數據作為樣本,這些數據將會存在著一定的分布規律,我們才能大膽地根據樣本數據對總體的情況進行大膽而有把握的判斷和推理……因此,簡而言之,當你能理解這些分布的時候,至少讓你在根據數據結果做出推斷的時候,對自己所得出的結論堅信不疑。
好了,解答完學習必要性的疑惑后,終于要進入正題了。
1.正態分布(Normal Distribution)
第一個我們要討論的概念就是正態分布,正態分布是所有概率分布中最重要的形式,如果沒有它,也就沒有接下來的那幾個分布。正態分布的特征表明被測事物處于穩定的狀態下,測量數據的波動是由于偶然因素引起的,所以在實踐中有廣泛的應用。在穩定的系統環境(如自然、人類社會等),許多事物和現象都會服從正態分布,例如人的身高、體重和智商;各種商品的尺寸和質量;自然環境的溫度、濕度和降雨量;考試的成績等。正態分布的重要性還體現在用樣本數據來推斷總體時,當樣本的數量足夠大的時,可以利用樣本的某些特征數據服從正態分布,進行推斷,獲得準確的結果。
正態分布一般記作? x~N(μ, σ^2),它的分布函數表達式為?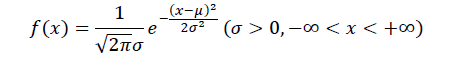
其中,π是圓周率;e是自然對數的底;x為隨機變量的取值;μ為正態分布的均值(期望),σ^2是正態分布的方差。
正態分布的函數圖像是一條“中間高,兩端低,左右對稱的曲線”(如下圖所示)。
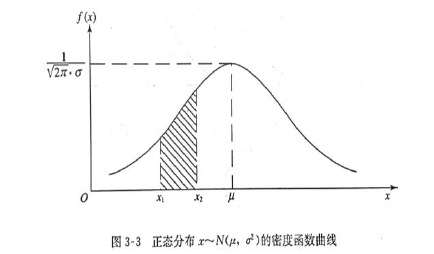
特別的,當μ=0,σ^2=1時,我們稱X服從標準正態分布:X~N(0,1).
由于其分布函數比較復雜,函數圖像將隨著不同的和方差發生著變化,人們將一般的正態分布進行標準化,即對于一般的正態分布x~N(μ, σ^2),只要令Z=(x-μ)/σ,則轉化為標準正態分布 Z~N(0,1).為了便于計算,人們制作出相應的數值表,方便對不同的數據代入值進行查詢,這就是標準正態分布表(如下表)。

正態分布表是我們學習教育統計到目前為止接觸到的第一個表,它比較特殊,每一個Z值都會對應一個Y值和P值,其中P值是我們比較關心的,也就是概率大小,如圖所示,當Z_0=1.00的時候,直線Z=0,直線Z=1,正態曲線以及Z軸所圍成的面積(也就是陰影部分)的概率大小為0.34134,寫成數學表達式則為P{Z≤1.00}=0.34134。由于正態曲線是對稱的,因此正態分布表所能查到的數據只有非負數,至于Z負半軸部分則很容易根據正半軸的情況進行推算。
利用正態分布以及標準正態分布表還有許多其他的實際應用,如將原始分轉化為標準分數;根據錄取率計算錄取的上線分數等。關于正態分布的內容就先介紹這么多,如有興趣的可以參考相關書籍深入了解。(張敏強.《教育與心理統計學》[M].北京:人民教育出版社,2010,11:88-100)
正態分布部分性質的證明:

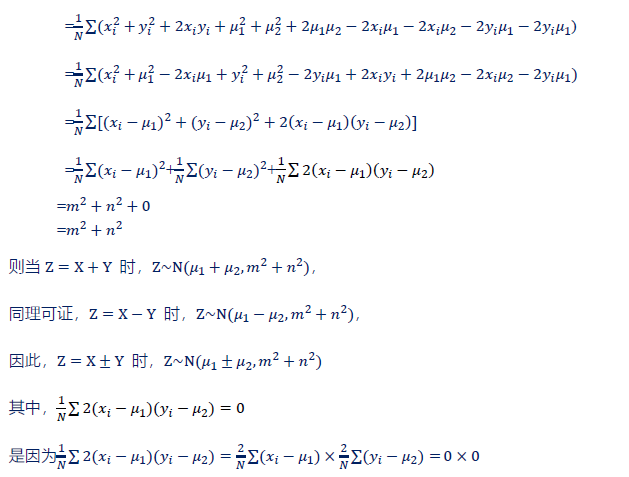

2. 均值分布(Meandistribution)(μ分布,? μ-distribution)
現在開始討論第二個分布,第一個分布是正態分布,正態分布是自然環境或者人類社會中普遍存在的數據分布特征,那么均值分布又是怎么來的呢?顧名思義,只要你從總體中隨機抽取若干組(如m)相同容量(如n)的數據,然后將每一組都求平均值,那么這m個平均值的分布情況就形成了均值分布(它的標準化形式稱為μ分布),而這樣的均值分布在一般情況下和正態分布的特征基本一致,因此均值分布也是正態分布,只是它的形狀一般會比總體更往對稱軸靠攏了而已。
那么,如果用數學語言來描述它的定義,即為設X服從正態分布,其均值為μ,方差為σ^2,則X~N(μ ,σ^2 ?),設x_1,x_2,…,x_n是總體X抽取的隨機樣本,則X?=1/n ∑_(i=1)^n?x_i 樣本的平均數。由于從總體中可以抽出多組的容量為n的樣本,則存在多個X?,此時X ?也服從正態分布,平均數為μ,方差為σ^2/n, 記作X?~(μ,σ^2/n)
為方便查表,作變換,
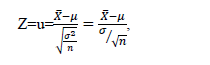
則Z~N(0,1)標準正態分布,又稱為Z分布,或u~N(0,1) , u分布。
對于均值分布,我們需要熟悉的是這個分布的均值μ和方差σ^2/n,標準差σ?√n,以及將一般均值分布轉化為標準正態分布的方法:Z=u=(X?-μ)/(σ?√n),然后能根據正態分布表查值即可。
由于均值分布通常會用來進行假設檢驗,我們會接觸到另外一個概念,顯著性水平α,那么α和標準正態曲線(Z表)有什么聯系呢?請看下圖(雙側檢驗為例),由于對稱和雙側檢驗,所以每邊的尾端陰影部分概率大小均為它的一半 α/2,它與標準正態分布表中的對應關系為α/2=0.5-P,也即P=0.5-α/2,我們可以很容易地根據正態分布表的近似P值查到相應的Z值和Y值。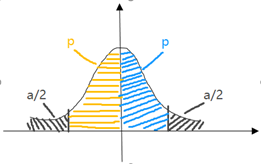
? ? ? U分布的簡單應用:

3.? 卡方(χ^2)分布(Chi-Square distribution)
卡方分布又是怎么來的呢?χ^2的符號就是“卡方分布”的縮寫記號而已,相當于一般函數的記號f(x)一樣,不能把它當作x^2!之所以卡方分布的符號記成平方的形式,是由于卡方分布的由來與平方有關,試看它的定義:
設X~N(0,1), x_1, x_2,…,x_n是總體X抽取的隨機樣本,則〖x_1〗^2+〖x_2〗^2+?+〖x_n〗^2是服從以n為自由度的χ^2分布,記作χ^2 ?~〖χ^2〗_((n)),自由度df=n.(自由度(degreeof freedom,df)就是所有類別中可以自由改變的類別數,在卡方分布中這n個樣本數據都是可以自由更換的,只要它們是來自N(0,1)總體就可以了。)
由此可知,卡方分布就是n項標準正態分布中抽出來的樣本數據的平方和的分布特征,它的密度函數為:

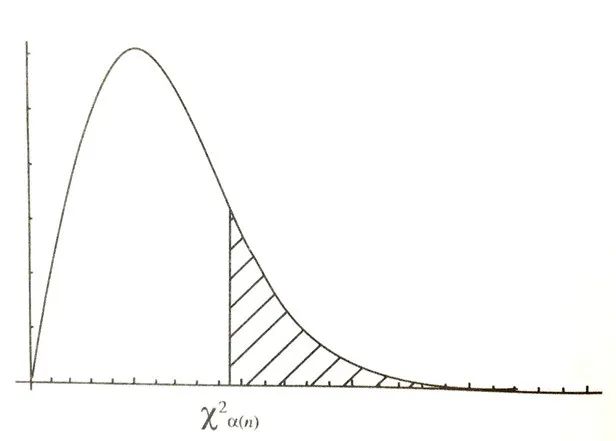
其中橫坐標表示卡方函數的取值x,,縱坐標表示x所對應的p(x)概率大小,概率密度圖像與橫坐標圍成的面積之和為1。卡方分布是一個正偏態分布(一般看函數圖像均值偏向小的一邊為正,偏向大的一邊為負)。隨著每次抽取的隨機變量X的個數不同,其分布的形狀會發生變化,n越小,分布偏斜;n越大,則會越接近于正態分布;當自由度n趨向無窮時,卡方分布即為正態分布。到此可見,無論是均值分布還是卡方分布,其圖像都與正態分布存在著千絲萬縷的聯系。
由于卡方分布密度函數計算比較復雜,因而人們編制了χ^2分布表,表中列出了χ^2變量在不同自由度下的臨界值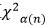 (單側) [如果是雙側檢驗,為了便于記憶,則記一邊為
(單側) [如果是雙側檢驗,為了便于記憶,則記一邊為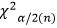 ,另一邊為
,另一邊為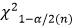 ,因為它的函數圖像并不對稱,因此不能將兩邊陰影部分的面積都當成是α/2]。
,因為它的函數圖像并不對稱,因此不能將兩邊陰影部分的面積都當成是α/2]。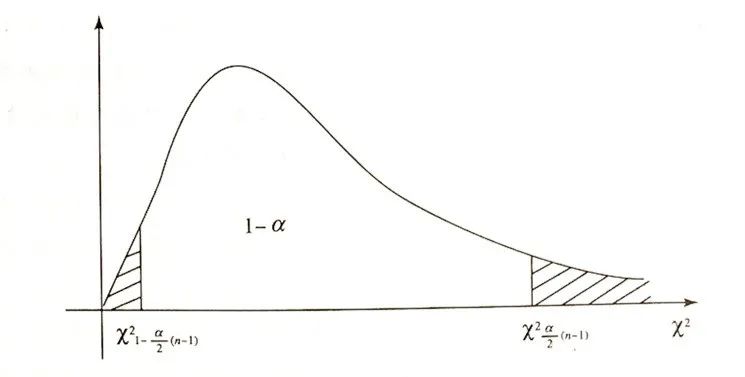
卡方分布多用于卡方檢驗,這部分內容將在后面學習非參數假設檢驗的時候進行深入介紹,目前需要掌握的就是能看懂卡方分布表,以及了解卡方統計量如何構造:如果樣本數據來自(標準)正態分布,則計算這些數據平方和的方法就可以視為一個卡方統計量。
例如,當對總體方差進行估計區間估計時。

如有興趣了解更多,還可訪問
https://www.statisticshowto.datasciencecentral.com/probability-and-statistics/chi-square/
4. t分布(t-distribution)
從卡方分布開始,我們就是通過構造統計量,從而得到相應的分布規律;同樣的,t分布的產生也是如此。結合參數估計的實際應用,對于t分布的由來,我更想將其與參數估計聯系在一起。
由前面的u分布可知,當總體方差σ^2未知時,要對總體的均值u進行估計,就需要利用u分布的基本性質,利用標準正態分布的轉化方法構造出統計量 Z=(X ?-μ)/(σ?√n),從而可以得到對總體均值進行區間估計的方法。
而如果總體方差σ^2未知,同樣要對總體的均值μ進行估計,那么又應該如何解決這個問題呢?我們看到,(X ?-μ)/(σ?√n)表達式中的σ此時也變成了未知,則沒辦法直接繼續使用上一種情況的方法構造出統計量,但是我們又知道,樣本的方差的調整值 S_(n-1)^2可以看成總體方差的一個無偏估計,那么就可以用這個無偏估計值來取代上一種情況統計量中的σ,即(X ?-μ)/(S?√n),這樣一來,我們就引出了t分布統計量的基本形式:
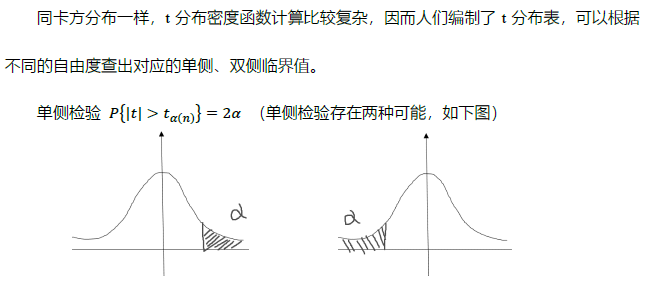

T分布在后面的假設檢驗中將扮演關鍵的作用,如相關樣本的 t檢驗、獨立樣本 t檢驗中都是對 t分布的實際應用。
如有興趣了解更多,還可訪問
https://www.statisticshowto.datasciencecentral.com/probability-and-statistics/t-test/
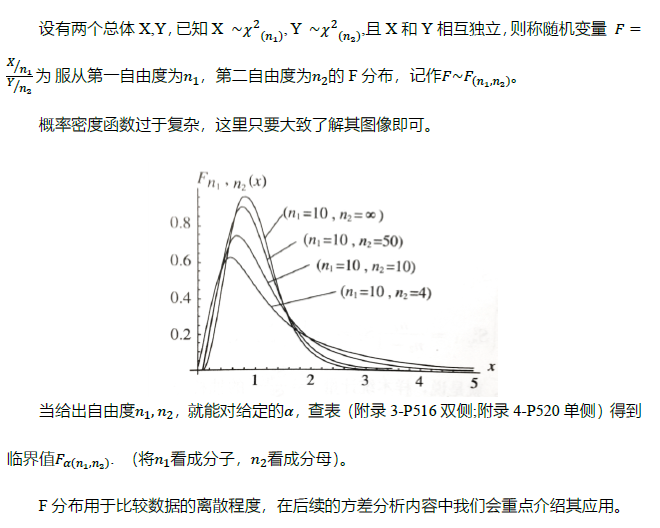
5. F分布( F-distribution)
?對于F分布,目前只要知道它的基本定義以及會查 F分布表就可以了。
如有興趣了解更多,還可訪問
https://www.thoughtco.com/f-distribution-3126583
由于編輯時間倉促,疏漏之處在所難免,如發現問題,歡迎批評指正!
參考文獻:
張敏強. 教育與心理統計學[M].北京:人民教育出版社,2010,11: 105-133.
劉新平 等. 教育統計與測評導論[M].北京:科學出版社,2013,11: 43-60.
[美]亞瑟?阿倫 等著,方雙虎 等譯. 心理統計學(第5版)[M].北京:中國人民大學出版社,2017,10:98-124.


)



)


...)



)





