一、麥克斯韋基于四元數觀點導出散度與旋度

已知的最早的關于散度和旋度的描述都來自麥克斯韋1873年的《A Treatise on Electricity and Magnetism》（電磁通論）一書。因此，為了探明散度和旋度的物理意義，有必要回到那本1873年的專著來看。

麥克斯韋的觀點（四元數觀點）

麥克斯韋很大程度上繼承了哈密頓的四元數觀點。四元數論認為，四維空間中的一點可以通過通過

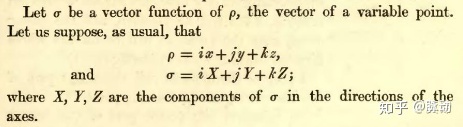
隨后，麥克斯韋對

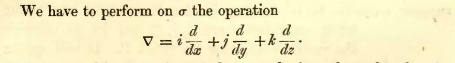
根據四元數的乘法規則，

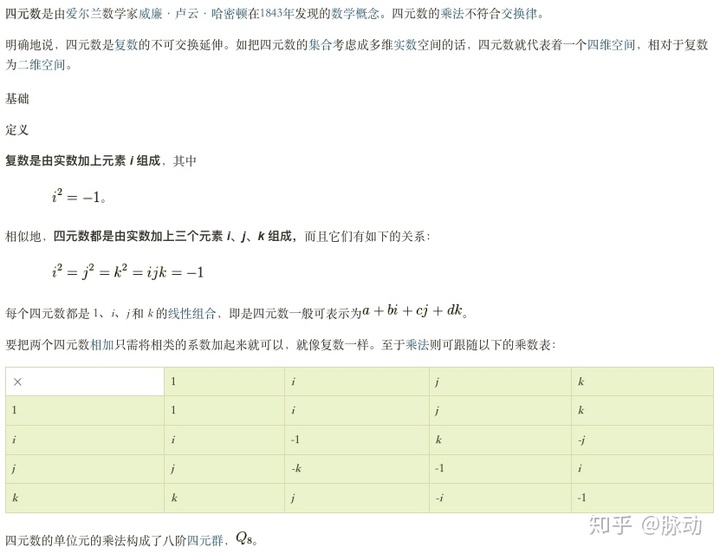
可以得到所乘結果的標量部和向量部分別是

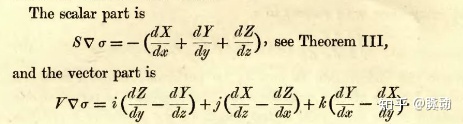
麥克斯韋發現，算子的標量部和向量部分別可以和兩個定理對應起來。這兩個定理就是位于其書中鋪墊部分的第21節的定理三

通量指向一個閉合曲面內部的面積分，可以表示成在曲面內部所求散度的體積分

以及第24節的定理四

沿一條閉合曲線計算的一個線積分，可以用以該曲線為邊的一個曲面上的面積分表示出來。

其實這兩個定理就是高數中的高斯公式（將閉合曲面積分換成體積分）和斯托克斯公式（將環路線積分換成曲面積分）。
也就是說，麥克斯韋的思路是：通過數學計算證明高斯公式和斯托克斯公式 → 通過四元數計算得到

麥克斯韋認為，標量部的結果可以這么解釋。假設
麥克斯韋建議把算子的標量部稱為 convergence（散度）。早期教材也有稱為斂度的。

至于算子的向量部，麥克斯韋認為，可以假設從該向量的方向來看。同樣地，審視

麥克斯韋建議把算子的向量部稱為 curl 或 version（旋度）。

參考：知乎解答 和 四元數的運算規則

二、現代電動力學里的物理意義

1. 矢量場
   的散度

設閉合曲面

圍著體積

，當

時，

對

的

通量與

之比的極限稱為

的散度，即

2. 矢量場

設閉合曲線

圍著面積

，當

時，

對

的環量與

之比的極限稱為

的旋度沿著該面法線的分量，即

3. 標量場

設沿線元

上，標量場

的數值改變

，

稱為梯度沿著

方向上的分量，即

4. 由以上定義可得積分變換

于是在直角坐標系中利用微分算子

參考：《電動力學》

三、數學上的總結

矢量微分算子

在

1. 梯度

函數

2. 散度

矢量

3. 旋度

矢量

4. 拉普拉斯算子

表示為

它作用于函數

它作用于矢量

5. 常用運算

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

梯度的旋度為零

(10)

旋度的散度為零

(11)

參考：漁樵《數學物理方法》

四、 一些不同的解釋

（1）通量是單位時間內通過的某個曲面的量；散度是通量強度。

環流量是單位時間內環繞的某個曲線的量；旋度是環流量強度。

（2）散度：單位體積的通量。旋度：單位面積的環量。梯度：單位長度的變量。

（3）散度是閉合曲面圍成空間中的通量除以圍成空間體積，然后令曲面無限小。

旋度是閉合曲線圍成面積中的環流除以圍成范圍面積，然后令曲線無限小。（這個閉合曲線圍成的面要選擇環流最大的那個面，而旋度的方向就是這個最大面的法線方向）

（4）從物理的角度這樣理解：

散度就是點電荷的電量密度，可以通過對電量密度的體積分求電通量，反之亦然；

旋度就是導線的電流密度，可以通過對電流密度面積分求圍繞導線一圈的磁場強度的閉合環路積分，反之亦然。同時旋度方向可理解為導線的電流方向。

（5）看了回答，感覺都沒有回答到物理問題的核心。

不管是經典力學還是量子力學梯度對應的是空間動量，旋度對應的是空間角動量。
所有矢量都可以化為梯度場和旋度場。此即霍姆赫茲定理。梯度場的旋度為零，對應動量守恒。旋度場的散度為零，對應角動量守恒。

（6）流體力學

Divergence(散度)和Curl(旋度)的主要作用目前看來好像就是方便積分，其中Divergence Theorem和Stokes Theorem可以轉化散度和旋度的復雜的積分到簡單一點的形式。(其實也不是每一個轉了之后都變得更好的)
物理上的理解也許采用流體力學的版本較好，一個點的散度測量水流流進和流出這個點的速率，一個點的旋度測量這個點水流旋轉的快慢。

參考：知乎解答