- 目錄:
- 1、使用場景
- 2、優缺點
- 3、算法原理
- 3.1、傳統向量空間模型的缺陷
- 3.2、Latent Semantic Analysis (Latent Semantic Indexing)
- 3.3、算法實例
- 4、文檔相似度的計算
- 5、對應的實踐Demo
目錄:
1、使用場景
文本挖掘中,主題模型。聚類算法關注于從樣本特征的相似度方面將數據聚類。比如通過數據樣本之間的歐式距離,曼哈頓距離的大小聚類等。而主題模型,顧名思義,就是對文字中隱含主題的一種建模方法。比如從“人民的名義”和“達康書記”這兩個詞我們很容易發現對應的文本有很大的主題相關度,但是如果通過詞特征來聚類的話則很難找出,因為聚類方法不能考慮到到隱含的主題這一塊。
那么如何找到隱含的主題呢?這個一個大問題。常用的方法一般都是基于統計學的生成方法。即假設以一定的概率選擇了一個主題,然后以一定的概率選擇當前主題的詞。最后這些詞組成了我們當前的文本。所有詞的統計概率分布可以從語料庫獲得,具體如何以“一定的概率選擇”,這就是各種具體的主題模型算法的任務了。當然還有一些不是基于統計的方法,比如我們下面講到的LSI。
潛在語義索引(LSI),又稱為潛在語義分析(LSA),主要是在解決兩類問題,一類是一詞多義,如“bank”一詞,可以指銀行,也可以指河岸;另一類是一義多詞,即同義詞問題,如“car”和“automobile”具有相同的含義,如果在檢索的過程中,在計算這兩類問題的相似性時,依靠余弦相似性的方法將不能很好的處理這樣的問題。所以提出了潛在語義索引的方法,利用SVD降維的方法將詞項和文本映射到一個新的空間。
2、優缺點
LSI是最早出現的主題模型了,它的算法原理很簡單,一次奇異值分解就可以得到主題模型,同時解決詞義的問題,非常漂亮。但是LSI有很多不足,導致它在當前實際的主題模型中已基本不再使用。
主要的問題有:
- SVD計算非常的耗時,尤其是我們的文本處理,詞和文本數都是非常大的,對于這樣的高維度矩陣做奇異值分解是非常難的。
- 主題值的選取對結果的影響非常大,很難選擇合適的k值。
- LSI得到的不是一個概率模型,缺乏統計基礎,結果難以直觀的解釋。
對于問題1,主題模型非負矩陣分解(NMF)可以解決矩陣分解的速度問題。對于問題2,這是老大難了,大部分主題模型的主題的個數選取一般都是憑經驗的,較新的層次狄利克雷過程(HDP)可以自動選擇主題個數。對于問題3,牛人們整出了pLSI(也叫pLSA)和隱含狄利克雷分布(LDA)這類基于概率分布的主題模型來替代基于矩陣分解的主題模型。
回到LSI本身,對于一些規模較小的問題,如果想快速粗粒度的找出一些主題分布的關系,則LSI是比較好的一個選擇,其他時候,如果你需要使用主題模型,推薦使用LDA和HDP。
3、算法原理
3.1、傳統向量空間模型的缺陷
向量空間模型是信息檢索中最常用的檢索方法,其檢索過程是,將文檔集D中的所有文檔和查詢都表示成以單詞為特征的向量,特征值為每個單詞的TF-IDF值,然后使用向量空間模型(亦即計算查詢q的向量和每個文檔di的向量之間的相似度)來衡量文檔和查詢之間的相似度,從而得到和給定查詢最相關的文檔。
向量空間模型簡單的基于單詞的出現與否以及TF-IDF等信息來進行檢索,但是“說了或者寫了哪些單詞”和“真正想表達的意思”之間有很大的區別,其中兩個重要的阻礙是單詞的多義性(polysems)和同義性(synonymys)。多義性指的是一個單詞可能有多個意思,比如Apple,既可以指水果蘋果,也可以指蘋果公司;而同義性指的是多個不同的詞可能表示同樣的意思,比如search和find。
同義詞和多義詞的存在使得單純基于單詞的檢索方法(比如向量空間模型等)的檢索精度受到很大影響。下面舉例說明:
假設用戶的查詢為Q=”IDF in computer-based information look-up”
存在三篇文檔Doc 1,Doc 2,Doc 3,其向量表示如下:

其中Table(i,j)=1表示文檔i包含詞語j。Table(i,j)=x表示該詞語在查詢Q中出現。Relevance如果為R表示該文檔實際上和查詢Q相關,Match為M表示根據基于單詞的檢索方法判斷的文檔和查詢的相關性。
通過觀察查詢,我們知道用戶實際上需要的是和“信息檢索”相關的文檔,文檔1是和信息檢索相關的,但是因為不包含查詢Q中的詞語,所以沒有被檢索到。實際上該文檔包含的詞語“retrieval”和查詢Q中的“look-up”是同義詞,基于單詞的檢索方法無法識別同義詞,降低了檢索的性能。而文檔2雖然包含了查詢中的”information”和”computer”兩個詞語,但是實際上該篇文檔講的是“信息論”(Information Theory),但是基于單詞的檢索方法無法識別多義詞,所以把這篇實際不相關的文檔標記為Match。
總而言之,在基于單詞的檢索方法中,同義詞會降低檢索算法的召回率(Recall),而多義詞的存在會降低檢索系統的準確率(Precision)。
3.2、Latent Semantic Analysis (Latent Semantic Indexing)
我們希望找到一種模型,能夠捕獲到單詞之間的相關性。如果兩個單詞之間有很強的相關性,那么當一個單詞出現時,往往意味著另一個單詞也應該出現(同義詞);反之,如果查詢語句或者文檔中的某個單詞和其他單詞的相關性都不大,那么這個詞很可能表示的是另外一個意思(比如在討論互聯網的文章中,Apple更可能指的是Apple公司,而不是水果) 。
LSA(LSI)使用SVD來對單詞-文檔矩陣進行分解。SVD可以看作是從單詞-文檔矩陣中發現不相關的索引變量(因子),將原來的數據映射到語義空間內。在單詞-文檔矩陣中不相似的兩個文檔,可能在語義空間內比較相似。
SVD,亦即奇異值分解,是對矩陣進行分解的一種方法,一個t*d維的矩陣(單詞-文檔矩陣)X,可以分解為T*S*DT,其中T為t*m維矩陣,T中的每一列稱為左奇異向量(left singular bector),S為m*m維對角矩陣,每個值稱為奇異值(singular value),D為d*m維矩陣,D中的每一列稱為右奇異向量。在對單詞文檔矩陣X做SVD分解之后,我們只保存S中最大的K個奇異值,以及T和D中對應的K個奇異向量,K個奇異值構成新的對角矩陣S’,K個左奇異向量和右奇異向量構成新的矩陣T’和D’:X’=T’*S’*D’T形成了一個新的t*d矩陣。
3.3、算法實例
這里舉一個簡單的LSI實例,假設我們有下面這個有11個詞三個文本的詞頻TF對應矩陣如下:
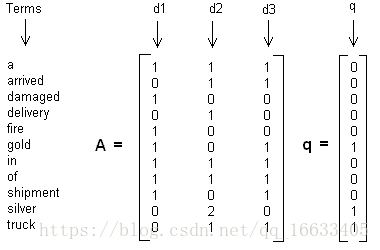
這里我們沒有使用預處理,也沒有使用TF-IDF,在實際應用中最好使用預處理后的TF-IDF值矩陣作為輸入。
我們假定對應的主題數為2,則通過SVD降維后得到的三矩陣為:
從矩陣Uk我們可以看到詞和詞義之間的相關性。而從Vk可以看到3個文本和兩個主題的相關性。大家可以看到里面有負數,所以這樣得到的相關度比較難解釋。
4、文檔相似度的計算
在上面我們通過LSI得到的文本主題矩陣即Vk可以用于文本相似度計算。而計算方法一般是通過余弦相似度。比如對于上面的三文檔兩主題的例子。我們可以計算第一個文本和第二個文本的余弦相似度如下 :
到這里也許你對整個過程也許還有點懵逼,為什么要用SVD分解,分解后得到的矩陣是什么含義呢?別著急下面將為你解答。
潛在語義索引(Latent Semantic Indexing)與PCA不太一樣,至少不是實現了SVD就可以直接用的,不過LSI也是一個嚴重依賴于SVD的算法,之前吳軍老師在矩陣計算與文本處理中的分類問題中談到:
“三個矩陣有非常清楚的物理含義。第一個矩陣X中的每一行表示意思相關的一類詞,其中的每個非零元素表示這類詞中每個詞的重要性(或者說相關性),數值越大越相關。最后一個矩陣Y中的每一列表示同一主題一類文章,其中每個元素表示這類文章中每篇文章的相關性。中間的矩陣則表示類詞和文章雷之間的相關性。因此,我們只要對關聯矩陣A進行一次奇異值分解,w 我們就可以同時完成了近義詞分類和文章的分類。(同時得到每類文章和每類詞的相關性)。”
上面這段話可能不太容易理解,不過這就是LSI的精髓內容,我下面舉一個例子來說明一下,下面的例子來自LSA tutorial,具體的網址我將在最后的引用中給出:
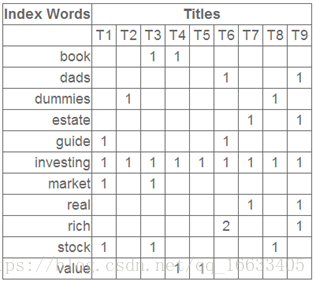
這就是一個矩陣,不過不太一樣的是,這里的一行表示一個詞在哪些title(文檔)中出現了(一行就是之前說的一維feature),一列表示一個title中有哪些詞,(這個矩陣其實是我們之前說的那種一行是一個sample的形式的一種轉置,這個會使得我們的左右奇異向量的意義產生變化,但是不會影響我們計算的過程)。比如說T1這個title中就有guide、investing、market、stock四個詞,各出現了一次,我們將這個矩陣進行SVD,得到下面的矩陣:
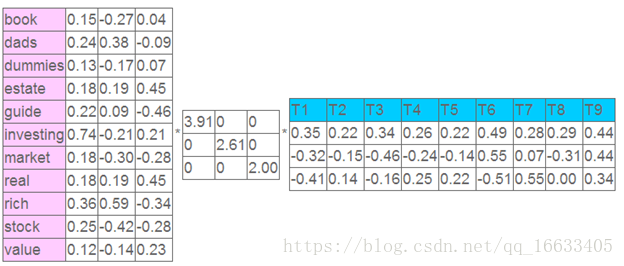
左奇異向量表示詞的一些特性,右奇異向量表示文檔的一些特性,中間的奇異值矩陣表示左奇異向量的一行與右奇異向量的一列的重要程序,數字越大越重要。
繼續看這個矩陣還可以發現一些有意思的東西,首先,左奇異向量的第一列表示每一個詞的出現頻繁程度,雖然不是線性的,但是可以認為是一個大概的描述,比如book是0.15對應文檔中出現的2次,investing是0.74對應了文檔中出現了9次,rich是0.36對應文檔中出現了3次;
其次,右奇異向量中一的第一行表示每一篇文檔中的出現詞的個數的近似,比如說,T6是0.49,出現了5個詞,T2是0.22,出現了2個詞。
然后我們反過頭來看,我們可以將左奇異向量和右奇異向量都取后2維(之前是3維的矩陣),投影到一個平面上,可以得到(如果對左奇異向量和右奇異向量單獨投影的話也就代表相似的文檔和相似的詞):
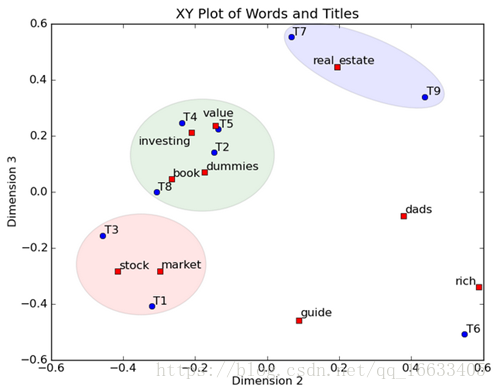
在圖上,每一個紅色的點,都表示一個詞,每一個藍色的點,都表示一篇文檔,這樣我們可以對這些詞和文檔進行聚類,比如說stock 和 market可以放在一類,因為他們老是出現在一起,real和estate可以放在一類,dads,guide這種詞就看起來有點孤立了,我們就不對他們進行合并了。按這樣聚類出現的效果,可以提取文檔集合中的近義詞,這樣當用戶檢索文檔的時候,是用語義級別(近義詞集合)去檢索了,而不是之前的詞的級別。這樣一減少我們的檢索、存儲量,因為這樣壓縮的文檔集合和PCA是異曲同工的,二可以提高我們的用戶體驗,用戶輸入一個詞,我們可以在這個詞的近義詞的集合中去找,這是傳統的索引無法做到的。
5、對應的實踐Demo
import jieba
from gensim import corpora, models
from gensim.similarities import Similarityjieba.load_userdict("userdict.txt")
stopwords = set(open('stopwords.txt',encoding='utf8').read().strip('\n').split('\n')) #讀入停用詞
raw_documents = ['0無償居間介紹買賣毒品的行為應如何定性','1吸毒男動態持有大量毒品的行為該如何認定','2如何區分是非法種植毒品原植物罪還是非法制造毒品罪','3為毒販販賣毒品提供幫助構成販賣毒品罪','4將自己吸食的毒品原價轉讓給朋友吸食的行為該如何認定','5為獲報酬幫人購買毒品的行為該如何認定','6毒販出獄后再次夠買毒品途中被抓的行為認定','7虛夸毒品功效勸人吸食毒品的行為該如何認定','8妻子下落不明丈夫又與他人登記結婚是否為無效婚姻','9一方未簽字辦理的結婚登記是否有效','10夫妻雙方1990年按農村習俗舉辦婚禮沒有結婚證 一方可否起訴離婚','11結婚前對方父母出資購買的住房寫我們二人的名字有效嗎','12身份證被別人冒用無法登記結婚怎么辦?','13同居后又與他人登記結婚是否構成重婚罪','14未辦登記只舉辦結婚儀式可起訴離婚嗎','15同居多年未辦理結婚登記,是否可以向法院起訴要求離婚'
]
corpora_documents = []
for item_text in raw_documents:item_str = jieba.lcut(item_text)print(item_str)corpora_documents.append(item_str)
# print(corpora_documents)
# 生成字典和向量語料
dictionary = corpora.Dictionary(corpora_documents)
print("dictionary"+str(dictionary))
# dictionary.save('dict.txt') #保存生成的詞典
# dictionary=Dictionary.load('dict.txt')#加載
# 通過下面一句得到語料中每一篇文檔對應的稀疏向量(這里是bow向量)
corpus = [dictionary.doc2bow(text) for text in corpora_documents]
# 向量的每一個元素代表了一個word在這篇文檔中出現的次數
print("corpus:"+str(corpus))
# corpora.MmCorpus.serialize('corpuse.mm',corpus)#保存生成的語料
# corpus=corpora.MmCorpus('corpuse.mm')#加載
# 測試數據
test_data_1 = '你好,我想問一下我想離婚他不想離,孩子他說不要,是六個月就自動生效離婚'
test_cut_raw_1 = jieba.lcut(test_data_1)print(test_cut_raw_1)
#轉化成tf-idf向量
# corpus是一個返回bow向量的迭代器。下面代碼將完成對corpus中出現的每一個特征的IDF值的統計工作
tfidf_model=models.TfidfModel(corpus)
corpus_tfidf = [tfidf_model[doc] for doc in corpus]
print(corpus_tfidf)
'''''
#查看model中的內容
for item in corpus_tfidf: print(item)
# tfidf.save("data.tfidf")
# tfidf = models.TfidfModel.load("data.tfidf")
# print(tfidf_model.dfs)
'''
#轉化成lsi向量
# lsi= models.LsiModel(corpus_tfidf,id2word=dictionary,num_topics=50)
lsi= models.LsiModel(corpus_tfidf,id2word=dictionary,num_topics=50)
corpus_lsi = [lsi[doc] for doc in corpus]
print("corpus_lsi:"+str(corpus_lsi))
similarity_lsi=Similarity('Similarity-Lsi-index', corpus_lsi, num_features=400,num_best=5)
# 2.轉換成bow向量 # [(51, 1), (59, 1)],即在字典的52和60的地方出現重復的字段,這個值可能會變化
test_corpus_3 = dictionary.doc2bow(test_cut_raw_1)
print(test_corpus_3)
# 3.計算tfidf值 # 根據之前訓練生成的model,生成query的IFIDF值,然后進行相似度計算
test_corpus_tfidf_3 = tfidf_model[test_corpus_3]
print(test_corpus_tfidf_3) # [(51, 0.7071067811865475), (59, 0.7071067811865475)]
# 4.計算lsi值
test_corpus_lsi_3 = lsi[test_corpus_tfidf_3]
print(test_corpus_lsi_3)
# lsi.add_documents(test_corpus_lsi_3) #更新LSI的值
print('——————————————lsi———————————————')
# 返回最相似的樣本材料,(index_of_document, similarity) tuples
print(similarity_lsi[test_corpus_lsi_3])
實驗結果:

可以看到返回的相似語句ID為15,14,2等還是和原輸入比較類似的。
參考:
https://www.cnblogs.com/kemaswill/archive/2013/04/17/3022100.html
https://www.cnblogs.com/pinard/p/6805861.html
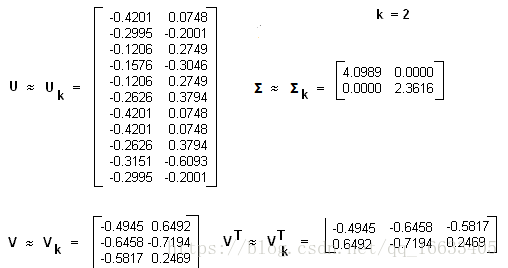
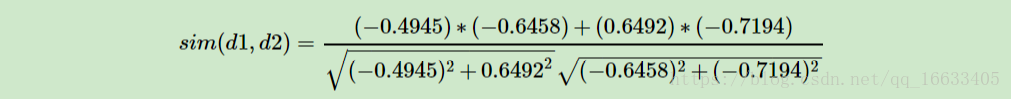







![[LeetCode]Basic Calculator](http://pic.xiahunao.cn/[LeetCode]Basic Calculator)








)


