文章目錄
- 目錄:
- 前言:
- 1、導數(曲線變化的快慢)、二階導數(曲線斜率變化的快慢特別是反映曲線的凸凹性)的概念。
- 2、常用的導數公式:
- 3、微分和積分的數學含義:
- 4、泰勒公式及含義
- 5、梯度的概念及數學含義:
- 6、概率和概率密度:
- 7、概率公式:
- 8、常見的概率分布(對應的公式、圖像以及期望E和方差D)
- 9、Sigmod函數的公式及函數圖像
- 10、知道古典概型(考慮兩件事:第一、基本事件的總數,第二、要發生的事件的解的空間有多大。)
目錄:
前言:
以下為自己在學習機器學習的過程中總結的所需的一些基本的數學知識,如有不足或錯誤請指出,會保持不斷的更新。
1、導數(曲線變化的快慢)、二階導數(曲線斜率變化的快慢特別是反映曲線的凸凹性)的概念。
2、常用的導數公式:
3、微分和積分的數學含義:
微分對應的是導數、積分對應的是面積。除此之外要了解對應的常見的計算操作如分部積分操作等。
4、泰勒公式及含義
數學中,泰勒公式是一個用函數在某點的信息描述其附近取值的公式。如果函數足夠平滑的話,在已知函數在某一點的各階導數值的情況之下,泰勒公式可以用這些導數值做系數構建一個多項式來近似函數在這一點的鄰域中的值。泰勒公式還給出了這個多項式和實際的函數值之間的偏差。
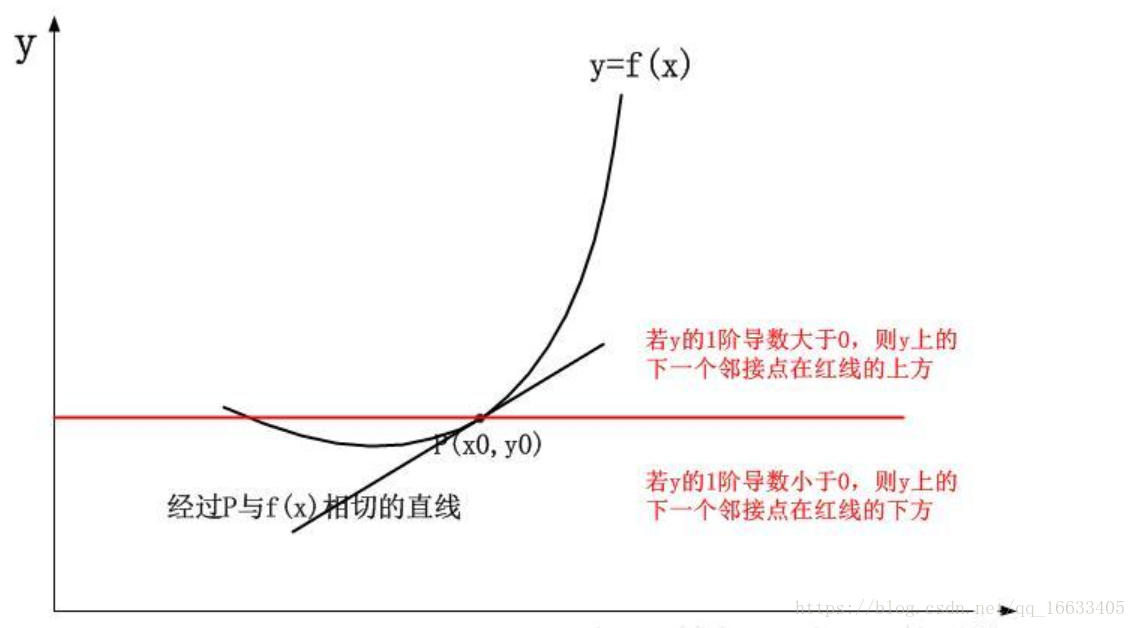
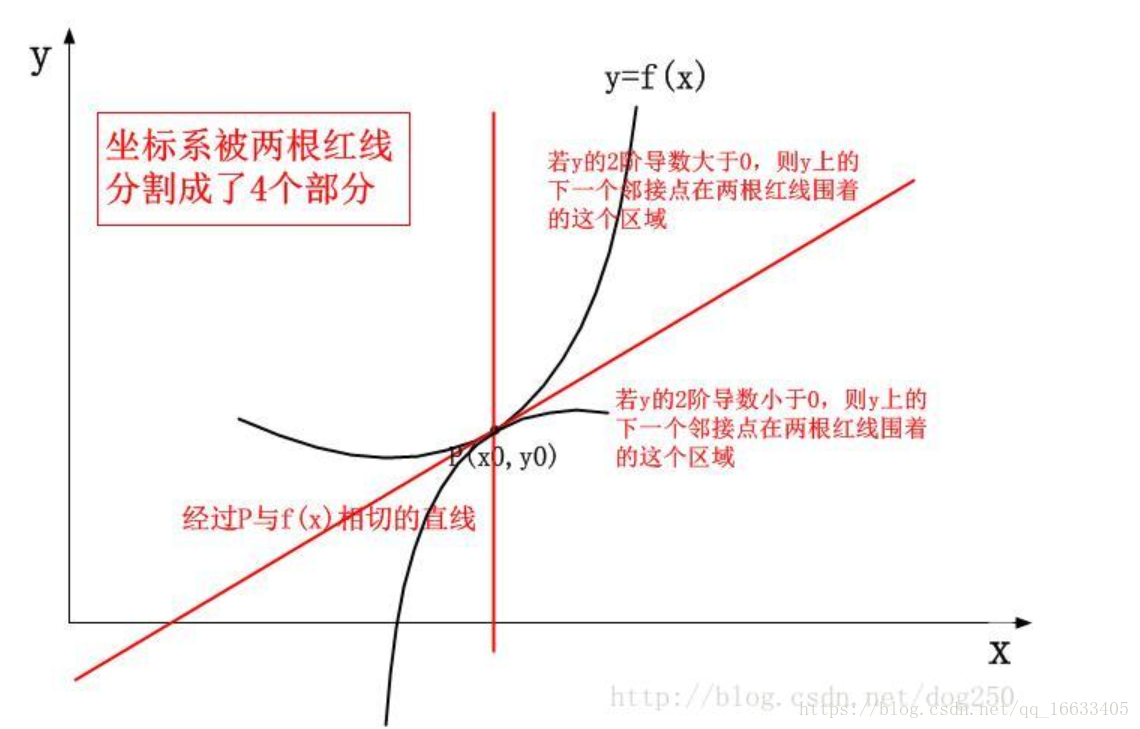
一句話說明泰勒公式的含義:用多項式函數取逼近光滑函數。實質通過計算函數在一個點的一階導數(判斷是遞增或遞減)、二階導數(進一步判斷一階導數的導數,即函數式增的越來越快還是減的越來越快)、三階導數(進一步判斷二階導數…)的值,來不斷的精確(預測)曲線的走勢,最終逼近光滑的境界。如下圖所示:
5、梯度的概念及數學含義:
梯度的本意是一個向量(矢量),表示某一函數在該點處的方向導數沿著該方向取得最大值,即函數在該點處沿著該方向(此梯度的方向)變化最快,變化率最大(為該梯度的模)
6、概率和概率密度:
概率針對的是變量為離散的情況,概率密度指的的是變量為連續的情況。
7、概率公式:
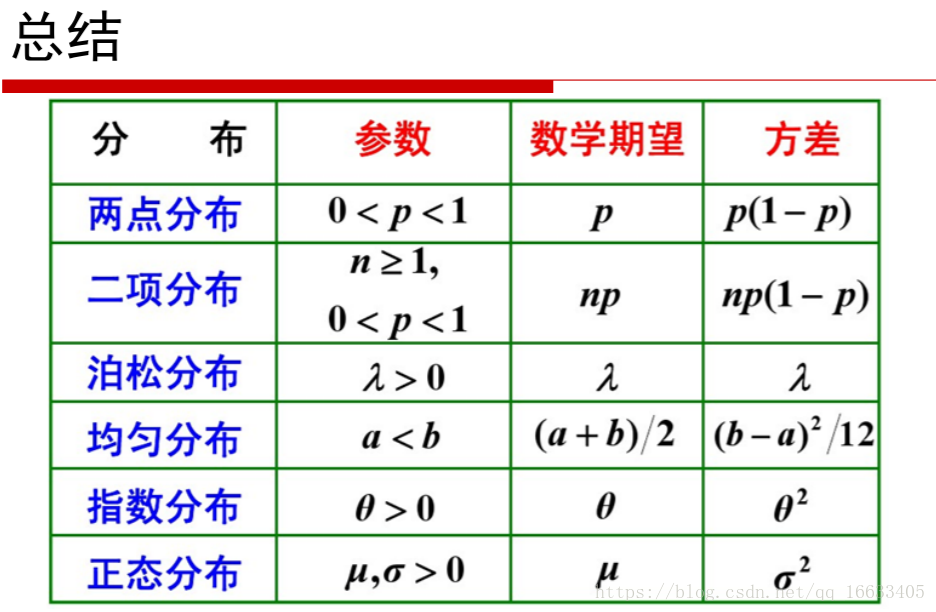
8、常見的概率分布(對應的公式、圖像以及期望E和方差D)
知道什么是泊松分布:當一件事以固定的速率獨立的出現時稱該事件服從泊松分布
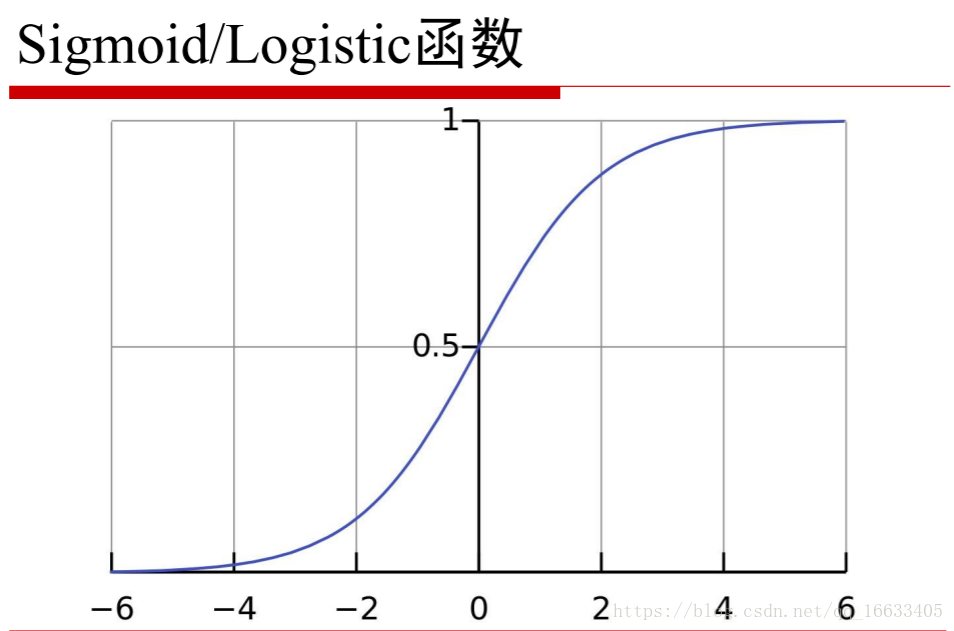
9、Sigmod函數的公式及函數圖像

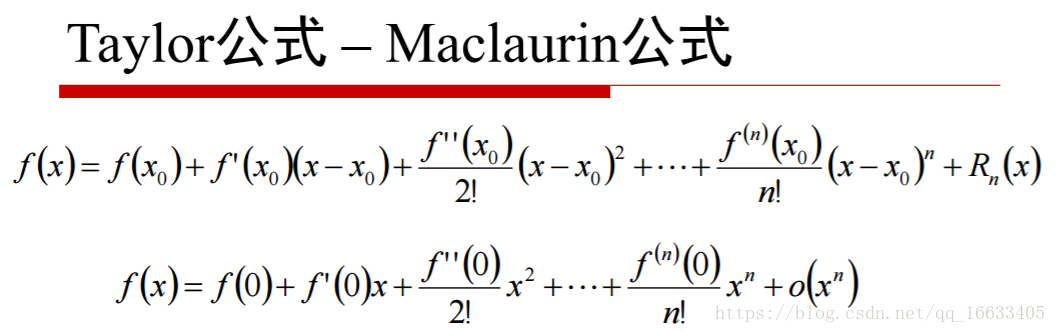


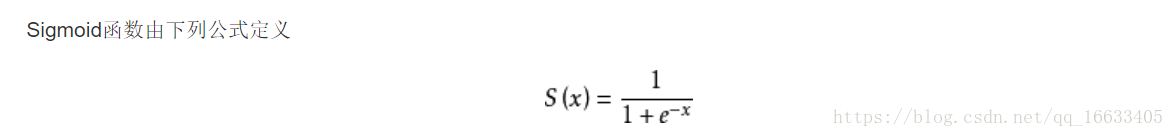
)



)



(分HA集群))
 C 模擬,思維)









