特征工程

? ? ? ?上周參加了學校的數據挖掘競賽，總的來說，在還需要人工干預的機器學習相關的任務中，主要解決兩個問題：（1）如何將原始的數據處理成合格的數據輸入（2）如何獲得輸入數據中的規律。第一個問題的解決方案是：特征工程。第二個問題的解決辦法是：機器學習。

?????? 相對機器學習的算法而言，特征工程的工作看起來比較low，但是特征工程在機器學習中非常重要。特征工程，是機器學習系列任務中最耗時、最繁重、最無聊卻又是最不可或缺的一部分。這些工作先行者們已經總結的很好，作為站在巨人的肩膀上的后來者，對他們的工作表示敬意。主要內容轉載自http://www.cnblogs.com/jasonfreak/p/5448385.html

這篇文章在該文章的基礎上做了添加或修改，仍在更新中

特征工程

1、特征工程是什么：

?????? 工業界流傳者這么一句話：數據和特征決定了機器學習的上限，而模型和算法只是逼近這個上限而已。

?????? 那么，到底什么是特征工程？我們知道，數據是信息的載體，但是原始的數據包含了大量的噪聲，信息的表達也不夠簡練。因此，特征工程的目的，是通過一系列的工程活動，將這些信息使用更高效的編碼方式（特征）表示。使用特征表示的信息，信息損失較少，原始數據中包含的規律依然保留。此外，新的編碼方式還需要盡量減少原始數據中的不確定因素（白噪聲、異常數據、數據缺失…等等）的影響。

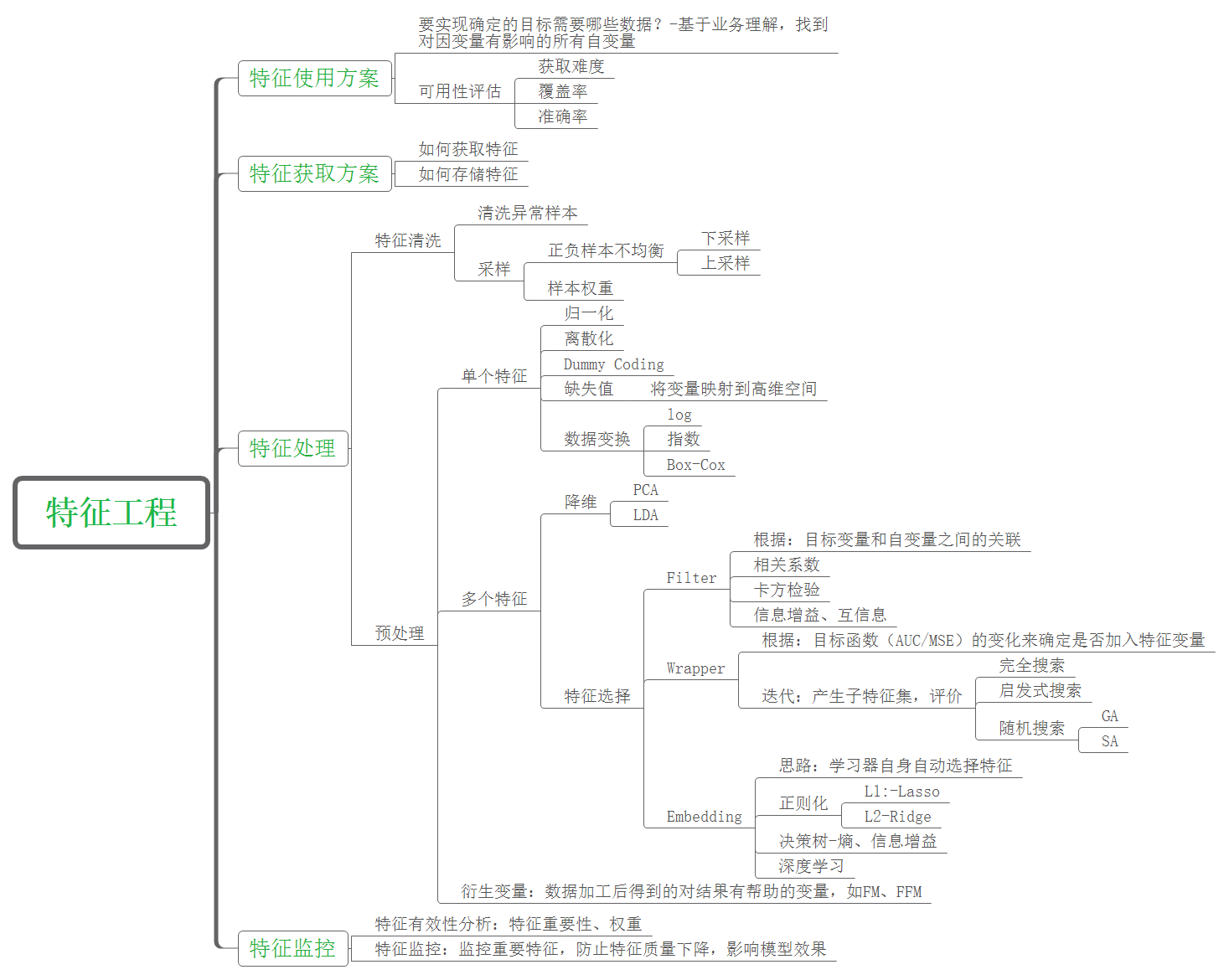
?????? 經過前人的總結，特征工程已經形成了接近標準化的流程，如下圖所示：

??

2、異常數據的清洗和樣本的選取

異常數據的清洗，目標是將原始數據中異常的數據清除。?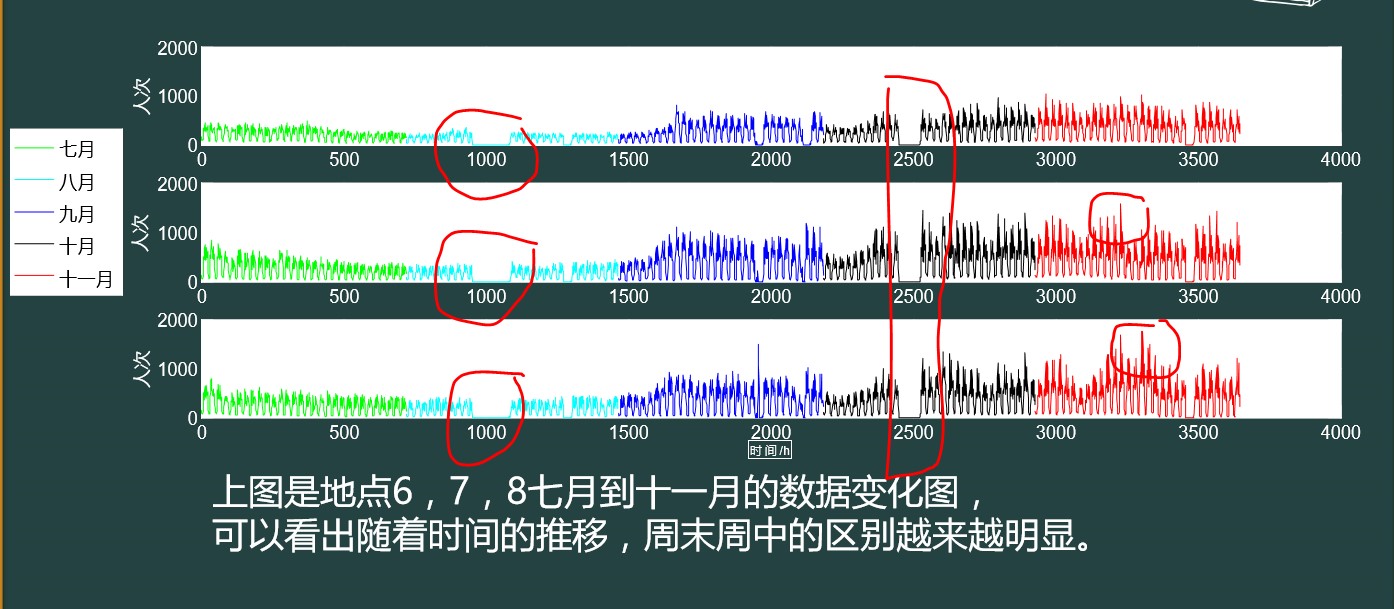

上圖表示了2015年7月到11月某個地點人流量的變化。數據的分析圖可以看到，紅色的框框內表示了數據的缺失和異常的峰值。這些異常的數據需要在特征的預處理前清除。一般情況下，直接將這些數據舍棄。

除了使用肉眼觀察的辦法來判斷數據的合理性，工業中，更多采用算法或者公式對數據的是否異常進行判斷。

（1）??? 結合業務情況進行過濾：比如去除crawler抓取，spam，作弊等數據

（2）??? 異常點檢測采用異常點檢測算法對樣本進行分析，常用的異常點檢測算法包括

2?? 偏差檢測：聚類、最近鄰等

2?? 基于統計的異常點檢測

例如極差，四分位數間距，均差，標準差等，這種方法適合于挖掘單變量的數值型數據。全距(Range)，又稱極差，是用來表示統計資料中的變異量數(measures of variation) ，其最大值與最小值之間的差距；四分位距通常是用來構建箱形圖，以及對概率分布的簡要圖表概述。

2?? 基于距離的異常點檢測

主要通過距離方法來檢測異常點，將數據集中與大多數點之間距離大于某個閾值的點視為異常點，主要使用的距離度量方法有絕對距離 ( 曼哈頓距離 ) 、歐氏距離和馬氏距離等方法。

2?? 基于密度的異常點檢測

考察當前點周圍密度，可以發現局部異常點，例如LOF算法

3、數據預處理

通過特征提取，我們能得到未經處理的特征，這時的特征可能有以下問題：

2? 不屬于同一量綱：即特征的規格不一樣，不能夠放在一起比較。無量綱化可以解決這一問題。

2? 信息冗余：對于某些定量特征，其包含的有效信息為區間劃分，例如學習成績，假若只關心“及格”或不“及格”，那么需要將定量的考分，轉換成“1”和“0”表示及格和未及格。二值化可以解決這一問題。

2? 定性特征不能直接使用：某些機器學習算法和模型只能接受定量特征的輸入，那么需要將定性特征轉換為定量特征。最簡單的方式是為每一種定性值指定一個定量值，但是這種方式過于靈活，增加了調參的工作。通常使用獨熱編碼的方式將定性特征轉換為定量特征：假設有N種定性值，則將這一個特征擴展為N種特征，當原始特征值為第i種定性值時，第i個擴展特征賦值為1，其他擴展特征賦值為0。獨熱編碼的方式相比直接指定的方式，不用增加調參的工作，對于線性模型來說，使用獨熱編碼后的特征可達到非線性的效果。

2? 存在缺失值：缺失值需要補充。

2? 信息利用率低：不同的機器學習算法和模型對數據中信息的利用是不同的，之前提到在線性模型中，使用對定性特征獨熱編碼可以達到非線性的效果。類似地，對定量變量多項式化，或者進行其他的轉換，都能達到非線性的效果。

2? 特征缺失：在本次的比賽中，影響人流量的因素還有天氣、溫度…等等，而這些因素在原始數據中并不存在，因此，需要在數據預處理的時候，將這些影響因素添加進來。

3.1無量綱化

　　無量綱化使不同規格的數據轉換到同一規格。常見的無量綱化方法有標準化和區間縮放法。標準化的前提是特征值服從正態分布，標準化后，其轉換成標準正態分布。區間縮放法利用了邊界值信息，將特征的取值區間縮放到某個特點的范圍，例如[0, 1]等。

3.1.1標準化

　　常用的方法是z-score標準化，經過處理后的數據均值為0，標準差為1，處理方法是：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?$x'=\frac{x-\mu}{\delta}$? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （1）

公式一中，x’是標準化后的特征，x是原始特征值， 是樣本均值， 是樣本標準差。它們可以通過現有樣本進行估計。在已有樣本足夠多的情況下比較穩定，適合現代嘈雜大數據場景。

3.1.2 區間縮放法

常用的方法是通過對原始數據進行線性變換把數據映射到[0,1]之間，變換函數為：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? $x'=\frac{x-\min}{\max-\min} $? ? ? ? ? ? ? ? ? ? ? ? ? ?（2）

　　其中?min 是樣本中最小值，?max是樣本中最大值，注意在數據流場景下最大值與最小值是變化的。另外，最大值與最小值非常容易受異常點影響，所以這種方法魯棒性較差，只適合傳統精確小數據場景。

3.1.3歸一化

簡單來說，標準化是依照特征矩陣的列處理數據，其通過求z-score的方法，將樣本的特征值轉換到同一量綱下。歸一化是依照特征矩陣的行處理數據，其目的在于樣本向量在點乘運算或其他核函數計算相似性時，擁有統一的標準，也就是說都轉化為“單位向量”。規則為 的歸一化公式如下：

? ? ? ? ? ? ? ?$x'=\frac{x}{\sqrt{\sum_j^m x^2_j}} $???????????????????????? ??????（3）

　　使用preproccessing庫的Normalizer類對數據進行歸一化的代碼如下：

3.2 對定量特征二值化（離散化）^[1]

　　定量特征二值化的核心在于設定一個閾值，大于閾值的賦值為1，小于等于閾值的賦值為0，公式表達如下：

? ? ? ? ? ? $x'=\left\{\begin{aligned}1&,& \ \ x>threshold\\0&,& x\leq threshold\end{aligned}\right.$? ? ? ? ? ? ? ? ? ? ? ? ? ?（4）

3.3 對定性特征進行獨熱編碼

?????? 獨熱編碼：使用一個二進制的位來表示某個定性特征的出現與否

3.4 缺失值的處理

??? 現實世界中的數據往往非常雜亂，未經處理的原始數據中某些屬性數據缺失是經常出現的情況。另外，在做特征工程時經常會有些樣本的某些特征無法求出。下面是幾種處理數據中缺失值的主要方法。

3.4.1. 刪除

最簡單的方法是刪除，刪除屬性或者刪除樣本。如果大部分樣本該屬性都缺失，這個屬性能提供的信息有限，可以選擇放棄使用該維屬性；如果一個樣本大部分屬性缺失，可以選擇放棄該樣本。雖然這種方法簡單，但只適用于數據集中缺失較少的情況。

3.4.2. 統計填充

對于缺失值的屬性，尤其是數值類型的屬性，根據所有樣本關于這維屬性的統計值對其進行填充，如使用平均數、中位數、眾數、最大值、最小值等，具體選擇哪種統計值需要具體問題具體分析。另外，如果有可用類別信息，還可以進行類內統計，比如身高，男性和女性的統計填充應該是不同的。

3.4.3. 統一填充

對于含缺失值的屬性，把所有缺失值統一填充為自定義值，如何選擇自定義值也需要具體問題具體分析。當然，如果有可用類別信息，也可以為不同類別分別進行統一填充。常用的統一填充值有：“空”、“0”、“正無窮”、“負無窮”等。

3.4.4 預測填充

我們可以通過預測模型利用不存在缺失值的屬性來預測缺失值，也就是先用預測模型把數據填充后再做進一步的工作，如統計、學習等。雖然這種方法比較復雜，但是最后得到的結果比較好。

3.4.5具體分析

上面兩次提到具體問題具體分析，為什么要具體問題具體分析呢？因為屬性缺失有時并不意味著數據缺失，缺失本身是包含信息的，所以需要根據不同應用場景下缺失值可能包含的信息進行合理填充。下面通過一些例子來說明如何具體問題具體分析，仁者見仁智者見智，僅供參考：

1. “年收入”：商品推薦場景下填充平均值，借貸額度場景下填充最小值；
2. “行為時間點”：填充眾數；
3. “價格”：商品推薦場景下填充最小值，商品匹配場景下填充平均值；
4. “人體壽命”：保險費用估計場景下填充最大值，人口估計場景下填充平均值；
5. “駕齡”：沒有填寫這一項的用戶可能是沒有車，為它填充為0較為合理；
6. ”本科畢業時間”：沒有填寫這一項的用戶可能是沒有上大學，為它填充正無窮比較合理；
7. “婚姻狀態”：沒有填寫這一項的用戶可能對自己的隱私比較敏感，應單獨設為一個分類，如已婚1、未婚0、未填-1。?

3.5 數據變換

　　常見的數據變換有基于多項式的、基于指數函數的、基于對數函數的。4個特征，度為2的多項式轉換公式如下：

$(x'_1,x'_2...x'_{15})=(1,x_1,x_2,x_3,x_4,x_1^2,x_1*x_2,x_1*x_3,x_1*x_4,x_2^2,x_2*x_3,x_2*x_4,x_3^2,x_3*x_4,x_4^2)$ ?（5）

?

多項式特征變換，目標是將特征兩兩組合起來，使得特征和目標變量之間的的關系更接近線性，從而提高預測的效果

4、特征選擇

當數據預處理完成后，我們需要選擇有意義的特征輸入機器學習的算法和模型進行訓練。通常來說，從兩個方面考慮來選擇特征：

• 特征是否發散：如果一個特征不發散，例如方差接近于0，也就是說樣本在這個特征上基本上沒有差異，這個特征對于樣本的區分并沒有什么用。
• 特征與目標的相關性：這點比較顯見，與目標相關性高的特征，應當優選選擇。除方差法外，本文介紹的其他方法均從相關性考慮。

　　根據特征選擇的形式又可以將特征選擇方法分為3種：

• Filter：過濾法，按照發散性或者相關性對各個特征進行評分，設定閾值或者待選擇閾值的個數，選擇特征。
• Wrapper：包裝法，根據目標函數（通常是預測效果評分），每次選擇若干特征，或者排除若干特征。
• Embedded：嵌入法，先使用某些機器學習的算法和模型進行訓練，得到各個特征的權值系數，根據系數從大到小選擇特征。類似于Filter方法，但是是通過訓練來確定特征的優劣。

　　我們使用sklearn中的feature_selection庫來進行特征選擇。

4.1 Filter

4.1.1 方差選擇法

　　使用方差選擇法，先要計算各個特征的方差，然后根據閾值，選擇方差大于閾值的特征。

4.1.2 相關系數法

　　使用相關系數法，先要計算各個特征對目標值的相關系數以及相關系數的P值。?

4.1.3 卡方檢驗

　　經典的卡方檢驗是檢驗定性自變量對定性因變量的相關性。假設自變量有N種取值，因變量有M種取值，考慮自變量等于i且因變量等于j的樣本頻數的觀察值與期望的差距，構建統計量：

?$x^2=\sum\frac{(A-E)^2}{E} $ ? ? ?（6）

　　這個統計量的含義簡而言之就是自變量對因變量的相關性。選擇卡方值排在前面的K個特征作為最終的特征選擇

4.1.4 互信息法

　　經典的互信息也是評價定性自變量對定性因變量的相關性的，互信息計算公式如下：

?$I(X:Y)=\sum_{x\in X}\sum_{y\in Y}p(x,y)log\frac{p(x,y)}{p(x)p(y)}$ ? （7）

　　同理，選擇互信息排列靠前的特征作為最終的選取特征

?

4.2 Wrapper

4.2.1 遞歸特征消除法

　　遞歸消除特征法使用一個基模型來進行多輪訓練，每輪訓練后，消除若干權值系數的特征，再基于新的特征集進行下一輪訓練。

?

4.3 Embedded

4.3.1 基于懲罰項的特征選擇法

　　使用帶懲罰項的基模型，除了篩選出特征外，同時也進行了降維。由于$L_1$范數有篩選特征的作用，因此，訓練的過程中，如果使用了$L_1$范數作為懲罰項，可以起到特征篩選的效果

4.3.2 基于樹模型的特征選擇法

　　訓練能夠對特征打分的預選模型：GBDT、RandomForest和Logistic Regression等都能對模型的特征打分，通過打分獲得相關性后再訓練最終模型；

? ? ?GBDT: http://breezedeus.github.io/2014/11/19/breezedeus-feature-mining-gbdt.html

4.4 特征組合

通過特征組合后再來選擇特征：如對用戶id和用戶特征最組合來獲得較大的特征集再來選擇特征，這種做法在推薦系統和廣告系統中比較常見

5、降維

當特征選擇完成后，可以直接訓練模型了，但是可能由于特征矩陣過大，導致計算量大，訓練時間長的問題，因此降低特征矩陣維度也是必不可少的。常見的降維方法除了以上提到的基于L1懲罰項的模型以外，另外還有主成分分析法（PCA）和線性判別分析（LDA），線性判別分析本身也是一個分類模型。PCA和LDA有很多的相似點，其本質是要將原始的樣本映射到維度更低的樣本空間中，但是PCA和LDA的映射目標不一樣：PCA是為了讓映射后的樣本具有最大的發散性；而LDA是為了讓映射后的樣本有最好的分類性能。所以說PCA是一種無監督的降維方法，而LDA是一種有監督的降維方法。

5.1 主成分分析法（PCA）

　　使用decomposition庫的PCA類選擇特征的代碼如下：

1from sklearn.decomposition import PCA

2

3#主成分分析法，返回降維后的數據

4#參數n_components為主成分數目

5 PCA(n_components=2).fit_transform(iris.data)

5.2 線性判別分析法（LDA）

　　使用lda庫的LDA類選擇特征的代碼如下：

1from sklearn.lda import LDA

2

3#線性判別分析法，返回降維后的數據

4#參數n_components為降維后的維數

5 LDA(n_components=2).fit_transform(iris.data, iris.target)

參考文獻：

（1）維基百科

?

?