在做文本分析的時候,經常會到說將文本轉化為對應的向量,之后利用余弦定理來計算文本之間的相似度。但是最近在面試時,重復上面這句話,卻被面試官問到:“什么是余弦定理?”當時就比較懵逼,于是把余弦定理求文本相似度的過程敘述了一遍:“將樣本轉化為對應的空間中的兩個向量,然后計算兩個向量余弦值,之后根據余弦值的大小來判斷兩個樣本相似度有多少”,但是話音剛落就被面試官否定了,當時感覺自己說的是正確的,但是由于自己的確記不記得余弦定理的數學含義以及公式,所以也就沒有和面試官辯論,當時想請教下面試官他理解的余弦定理是什么,卻被一句“回去自己查”給堵死。。。之后對這件事一直耿耿于懷,不過又一想,也是,面試官問的是余弦定理,但是我說的是余弦定理在空間向量中如何計算相似度,好像是有點跑題。。。anyway,過去的已經過去了,只要有收獲就行。于是回來查了一下余弦定理是怎么應用于文本相似的度量的,下面是整個過程,其實很簡單,只不過當時把余弦定理的公式忘了,不然很容易就能解釋通(數學知識全還給老師了)。。。
相似度度量(Similarity),即計算個體間的相似程度,相似度度量的值越小,說明個體間相似度越小,相似度的值越大說明個體差異越大。
對于多個不同的文本或者短文本對話消息要來計算他們之間的相似度如何,一個好的做法就是將這些文本中詞語,映射到向量空間,形成文本中文字和向量數據的映射關系,通過計算幾個或者多個不同的向量的差異的大小,來計算文本的相似度。下面介紹一個詳細成熟的向量空間余弦相似度方法計算相似度
向量空間余弦相似度(Cosine Similarity)
余弦相似度用向量空間中兩個向量夾角的余弦值作為衡量兩個個體間差異的大小。余弦值越接近1,就表明夾角越接近0度,也就是兩個向量越相似,這就叫”余弦相似性”。
上圖兩個向量a,b的夾角很小可以說a向量和b向量有很高的的相似性,極端情況下,a和b向量完全重合。如下圖:
如上圖二:可以認為a和b向量是相等的,也即a,b向量代表的文本是完全相似的,或者說是相等的。如果a和b向量夾角較大,或者反方向。如下圖
如上圖三: 兩個向量a,b的夾角很大可以說a向量和b向量有很底的的相似性,或者說a和b向量代表的文本基本不相似。那么是否可以用兩個向量的夾角大小的函數值來計算個體的相似度呢?
向量空間余弦相似度理論就是基于上述來計算個體相似度的一種方法。下面做詳細的推理過程分析。
想到余弦公式,最基本計算方法就是初中的最簡單的計算公式,計算夾角θ的余弦定值公式為:
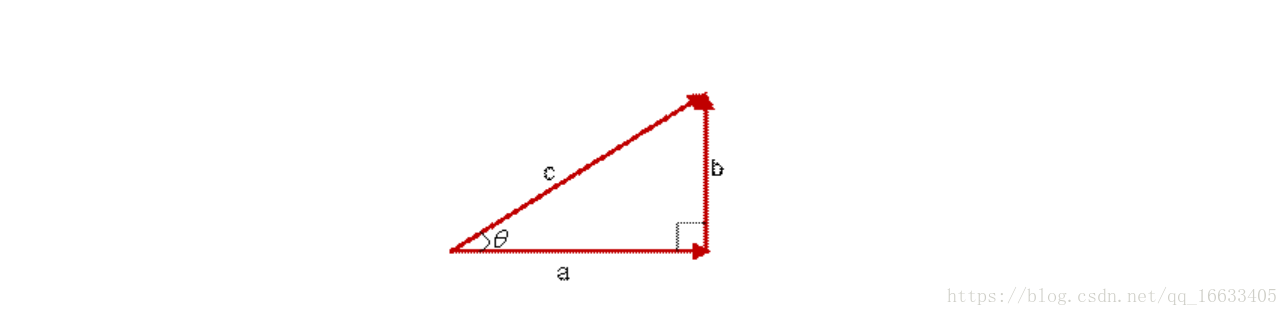
但是這個是只適用于直角三角形的,而在非直角三角形中,余弦定理的公式是
三角形中邊a和b的夾角 的余弦計算公式為:
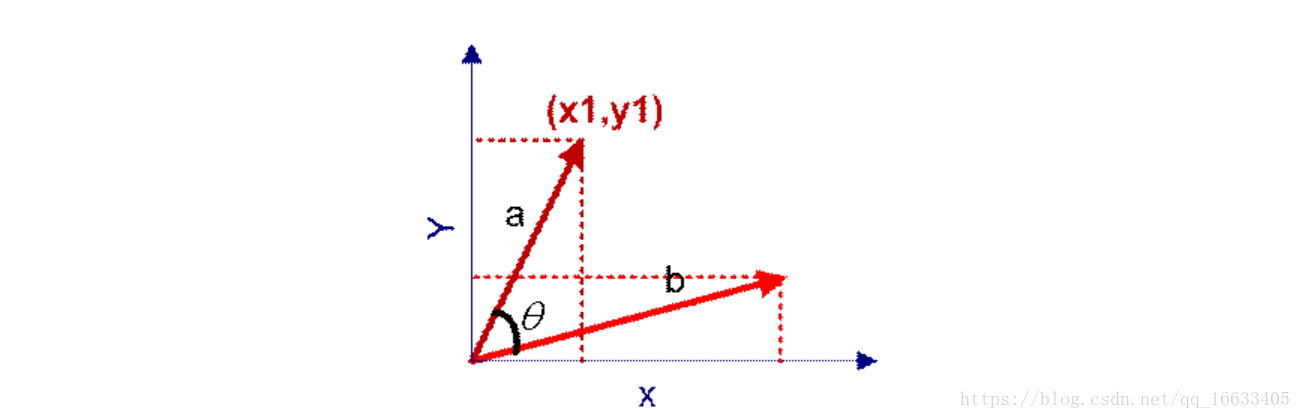
在向量表示的三角形中,假設a向量是(x1, y1),b向量是(x2, y2),那么可以將余弦定理改寫成下面的形式:
向量a和向量b的夾角 的余弦計算如下
擴展,如果向量a和b不是二維而是n維,上述余弦的計算法仍然正確。假定a和b是兩個n維向量,a是 ,b是 ,則a與b的夾角 的余弦等于:
余弦值越接近1,就表明夾角越接近0度,也就是兩個向量越相似,夾角等于0,即兩個向量相等,這就叫”余弦相似性”。
總結:
其實只要知道余弦定理余弦值的計算公式,然后轉化為空間中的兩個向量后,直接就能代入余弦定理來得到對應的余弦值,畢竟你知道兩個向量的坐標,也就意味著你知道了余弦定理公式中三角形的三條邊a、b、c的值。
參考:https://blog.csdn.net/u012160689/article/details/15341303





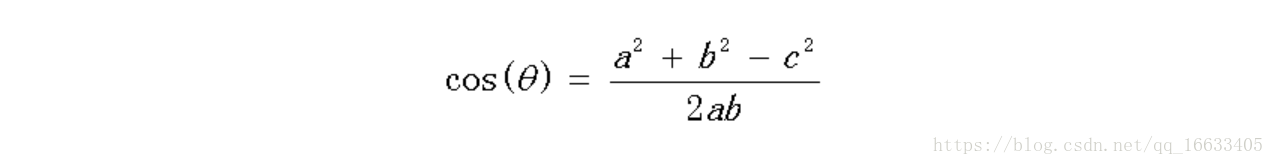
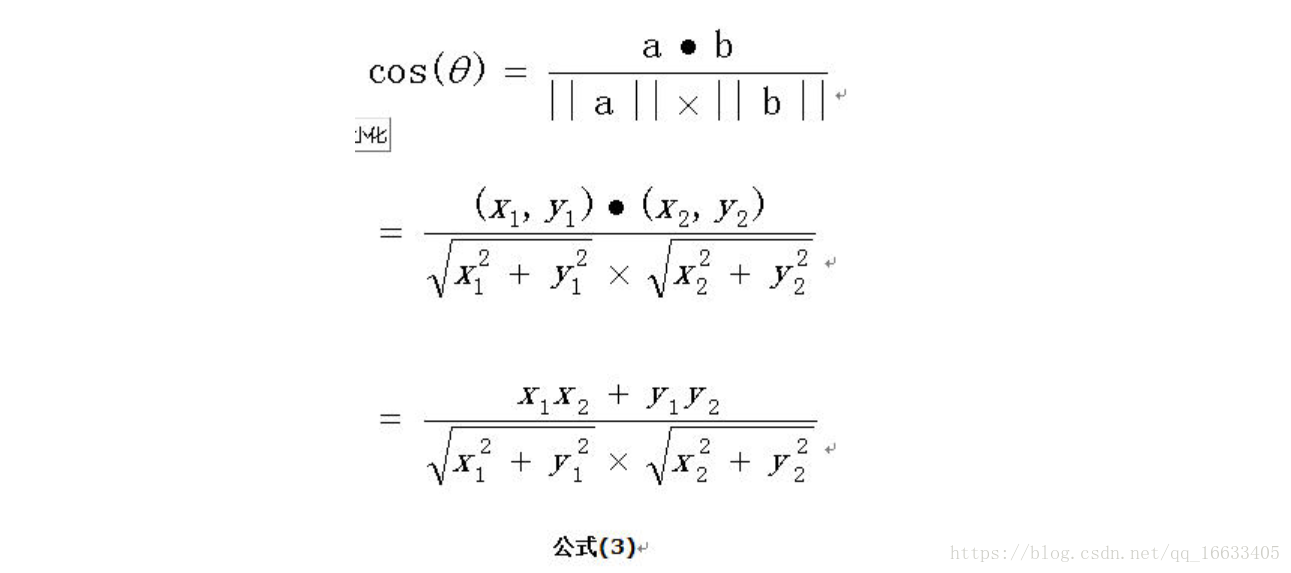
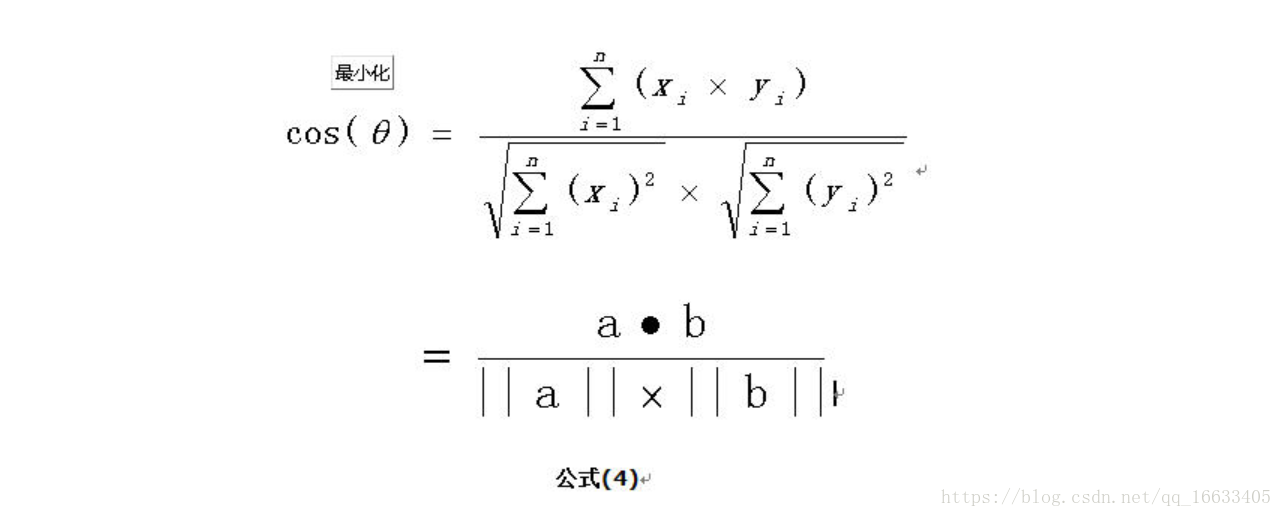






)



)



(分HA集群))
 C 模擬,思維)



