【bzoj2132】圈地計劃 網絡流最小割

題目描述

最近房地產商GDOI(Group of Dumbbells Or Idiots)從NOI(Nuts Old Idiots)手中得到了一塊開發土地。據了解，這塊土地是一塊矩形的區域，可以縱橫劃分為N×M塊小區域。GDOI要求將這些區域分為商業區和工業區來開發。根據不同的地形環境，每塊小區域建造商業區和工業區能取得不同的經濟價值。更具體點，對于第i行第j列的區域，建造商業區將得到Aij收益，建造工業區將得到Bij收益。另外不同的區域連在一起可以得到額外的收益，即如果區域(I,j)相鄰（相鄰是指兩個格子有公共邊）有K塊（顯然K不超過4）類型不同于(I,j)的區域，則這塊區域能增加k×Cij收益。經過Tiger.S教授的勘察，收益矩陣A,B,C都已經知道了。你能幫GDOI求出一個收益最大的方案么？

輸入

輸入第一行為兩個整數，分別為正整數N和M，分別表示區域的行數和列數；第2到N+1列，每行M個整數，表示商業區收益矩陣A；第N+2到2N+1列，每行M個整數，表示工業區收益矩陣B；第2N+2到3N+1行，每行M個整數，表示相鄰額外收益矩陣C。第一行，兩個整數，分別是n和m（1≤n，m≤100）；

任何數字不超過1000”的限制

輸出

輸出只有一行，包含一個整數，為最大收益值。

樣例輸入

3 3
1 2 3
4 5 6
7 8 9
9 8 7
6 5 4
3 2 1
1 1 1
1 3 1
1 1 1

樣例輸出

81

---

題解

網絡流最小割

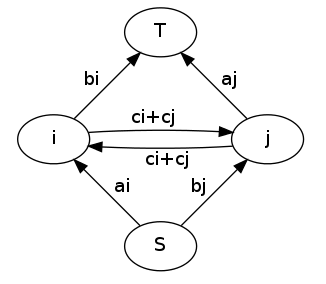
只考慮相鄰的兩個，問題轉化為：$i$和$j$各有兩種選法：選擇A可以獲得$a_i$或$a_j$的收益；選擇B可以獲得$b_i$或$b_j$的收益；如果選擇不同，則會獲得$c_i+c_j$的收益。問最大收益。

這是一個經典的最小割模型，建圖方法：S連向i，容量為$a_i$，i連向T，容量為b_i；S連向j，容量為$b_j$，i連向T，容量為$a_j$（這兩步是反轉源匯的過程）。i和j之間連容量為$c_i+c_j$的雙向邊。

?

因此總的建圖為：黑白染色，黑點正常連，白點反轉源匯，然后相鄰的點之間連邊。答案為$\sum\limits a_i+\sum\limits b_i+\sum\limits(c_i+c_j)-mincut$。

#include <queue>
#include <cstdio>
#include <cstring>
#define N 10010
#define M 1000010
#define pos(i , j) (i - 1) * m + j
using namespace std;
typedef long long ll;
const int inf = 1 << 30;
queue<int> q;
int n , m , head[N] , to[M] , next[M] , cnt = 1 , s , t , dis[N];
ll a[110][110] , b[110][110] , c[110][110] , val[M];
void add(int x , int y , ll z)
{to[++cnt] = y , val[cnt] = z , next[cnt] = head[x] , head[x] = cnt;to[++cnt] = x , val[cnt] = 0 , next[cnt] = head[y] , head[y] = cnt;
}
ll link(int x1 , int y1 , int x2 , int y2)
{add(pos(x1 , y1) , pos(x2 , y2) , c[x1][y1] + c[x2][y2]);add(pos(x2 , y2) , pos(x1 , y1) , c[x1][y1] + c[x2][y2]);return c[x1][y1] + c[x2][y2];
}
bool bfs()
{int x , i;memset(dis , 0 , sizeof(dis));while(!q.empty()) q.pop();dis[s] = 1 , q.push(s);while(!q.empty()){x = q.front() , q.pop();for(i = head[x] ; i ; i = next[i]){if(val[i] && !dis[to[i]]){dis[to[i]] = dis[x] + 1;if(to[i] == t) return 1;q.push(to[i]);}}}return 0;
}
ll dinic(int x , ll low)
{if(x == t) return low;ll temp = low , k;int i;for(i = head[x] ; i ; i = next[i]){if(val[i] && dis[to[i]] == dis[x] + 1){k = dinic(to[i] , min(temp , val[i]));if(!k) dis[to[i]] = 0;val[i] -= k , val[i ^ 1] += k;if(!(temp -= k)) break;}}return low - temp;
}
int main()
{int i , j;ll ans = 0;scanf("%d%d" , &n , &m) , s = 0 , t = n * m + 1;for(i = 1 ; i <= n ; i ++ ) for(j = 1 ; j <= m ; j ++ ) scanf("%lld" , &a[i][j]);for(i = 1 ; i <= n ; i ++ ) for(j = 1 ; j <= m ; j ++ ) scanf("%lld" , &b[i][j]);for(i = 1 ; i <= n ; i ++ ) for(j = 1 ; j <= m ; j ++ ) scanf("%lld" , &c[i][j]);for(i = 1 ; i <= n ; i ++ ){for(j = 1 ; j <= m ; j ++ ){ans += a[i][j] + b[i][j];if((i & 1) ^ (j & 1)) add(s , pos(i , j) , b[i][j]) , add(pos(i , j) , t , a[i][j]);else{add(s , pos(i , j) , a[i][j]) , add(pos(i , j) , t , b[i][j]);if(i > 1) ans += link(i , j , i - 1 , j);if(i < n) ans += link(i , j , i + 1 , j);if(j > 1) ans += link(i , j , i , j - 1);if(j < m) ans += link(i , j , i , j + 1);}}}while(bfs()) ans -= dinic(s , inf);printf("%lld\n" , ans);return 0;
}

?

?