4 正則化

4.1 概述

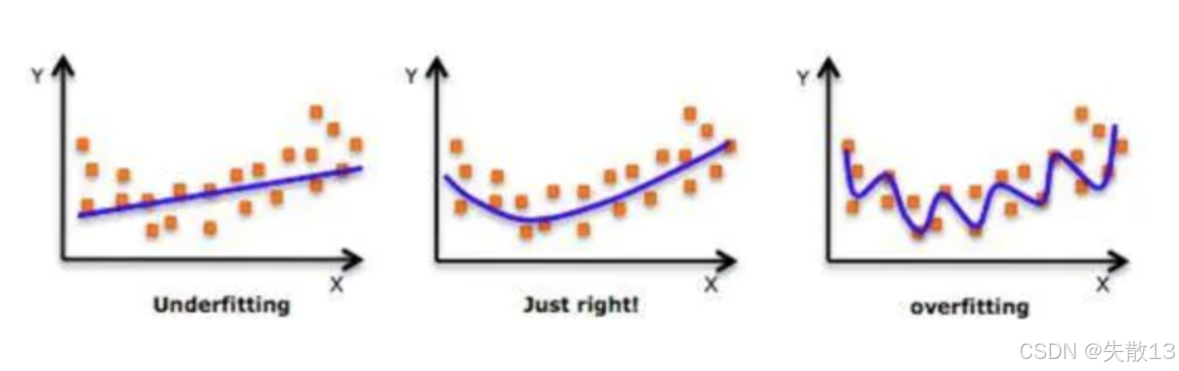
• 模型擬合的3種狀態

  

  • 左邊（Underfitting 欠擬合）：模型太簡單，沒抓住數據規律。比如用直線硬套彎曲的數據，預測效果差，訓練誤差和測試誤差都大；

  • 中間（Just right 擬合合適）：模型復雜度剛好，能捕捉數據趨勢，在訓練和新數據（測試）上表現都不錯，泛化能力強；

  • 右邊（Overfitting 過擬合）：模型太復雜，把訓練數據的“噪聲”都學進去了（比如個別點的隨機波動），看似訓練時誤差很小，但遇到新數據（測試）就“翻車”，泛化能力差；

• 正則化的核心目的：

  • “泛化能力”是機器學習的命門——模型不能只在訓練數據上表現好，得在沒見過的新數據上也準；
  • 正則化就是一系列“限制模型過度復雜、避免過擬合”的策略，讓模型更“穩健”；

• **為什么神經網絡特別需要正則化？**神經網絡（比如深度學習）的結構很靈活（多層、多參數），“表示能力”極強（能學超復雜規律），但也容易因為學太細（連噪聲都學）導致過擬合，所以必須用正則化“約束”它，平衡模型復雜度；

• 常見正則化策略

  • 范數懲罰（比如L1、L2正則）：給模型參數加“懲罰項”，讓參數不能太大/太極端，逼著模型簡化，避免“死記硬背”訓練數據；

  • Dropout：訓練時隨機“關掉”一部分神經元，讓模型不能過度依賴某些參數，相當于強制模型學更通用的規律；

  • 特殊網絡層（比如Batch Normalization，批量歸一化）：通過標準化等操作，讓每層輸入更穩定，間接限制模型復雜度，提升泛化能力。

4.2 Dropout正則化

• Dropout正則化的作用：

  • 神經網絡參數多、結構深，一旦訓練數據不夠，特別容易“過擬合”——模型死記硬背訓練數據的細節（甚至噪聲），但遇到新數據就完蛋；
  • Dropout 就是專門“治這個病”的：隨機讓部分神經元“失效”，逼著模型學更通用的規律，避免過擬合；

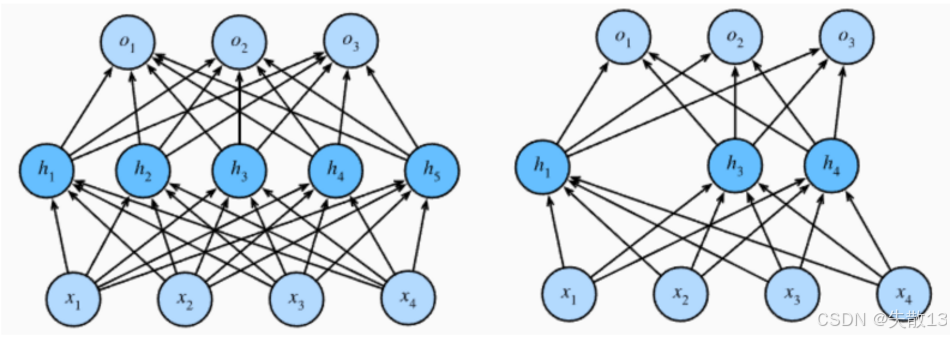
• 經過Dropout正則化的前后對比：

  • 左邊：原始神經網絡。所有神經元（$h_1$到$h_5$等）都工作，連接密密麻麻，模型復雜度高，容易過擬合；

  • 右邊：Dropout 生效后。隨機“關掉”了$h_2$、$h_5$等神經元（比如圖里淺色/消失的節點），相當于 臨時簡化網絡結構，每次訓練只用“子網絡”干活；

  

• Dropout 的具體操作（訓練時）

  • 隨機失活：訓練時，每個神經元有概率$p$（超參數，比如 0.5）被“關掉”（輸出置為 0），幸存的神經元要 按$1/(1?p)$縮放（保證整體輸出的期望不變）；

  • 子網絡訓練：每次訓練只用部分神經元（子網絡），參數只更新這部分。因為每次“關哪些神經元”是隨機的，模型被迫學更通用的特征，沒法死記硬背；

• 在測試時就不使用 Dropout。原因：

  • 測試是為了“穩定預測”，不能再隨機關神經元；
  • 所以測試時所有神經元都工作，但因為訓練時已經通過縮放補償，直接用完整網絡就能輸出可靠結果；

• 代碼：

  import torch
  import torch.nn as nndef test():# 初始化 Dropout 層，參數 p=0.4 表示每次訓練時，有 40% 的神經元會被隨機置零# Dropout 是正則化手段，通過隨機失活神經元，避免模型過擬合，提升泛化能力dropout = nn.Dropout(p=0.4)  # 生成輸入數據：# torch.randint(0, 10, size=[1, 4]) 生成一個形狀為 [1, 4] 的張量，元素是 0-9 的隨機整數# .float() 將整數張量轉換為浮點型，因為神經網絡計算通常使用浮點數inputs = torch.randint(0, 10, size=[1, 4]).float()  # 定義一個線性層（全連接層）：輸入維度 4，輸出維度 5# 線性層會做矩陣運算：y = Wx + b ，其中 W 是權重矩陣（4x5），b 是偏置（長度為5）layer = nn.Linear(4, 5)  # 讓輸入數據通過線性層，得到未經過 Dropout 的輸出# 此時輸出是線性層對輸入的直接變換結果，包含 5 個元素（因輸出維度是5）y = layer(inputs)  print("未失活FC層的輸出結果：\n", y)# 將線性層的輸出傳入 Dropout 層# 訓練模式下（默認），Dropout 會隨機把 40% 的輸出值置為 0，剩余 60% 的值會按 1/(1-0.4) 縮放（保證期望不變）# 測試/推理時一般會關閉 Dropout（通過 model.eval() 切換模式），避免結果隨機波動y = dropout(y)  print("失活后FC層的輸出結果：\n", y)test()
  

  

  • tensor([[ 0.8366, -0.5336, -2.7561, -1.7934, -2.0321]], grad_fn=<AddmmBackward0>)
    • 這是全連接層（nn.Linear）的直接輸出，5 個數值對應線性變換（y = Wx + b）的結果；
    • grad_fn=<AddmmBackward0> 表示這是由矩陣乘法（全連接層運算）產生的張量，支持自動求導；
  • tensor([[ 1.3944, -0.8893, -0.0000, -2.9890, -0.0000]], grad_fn=<MulBackward0>)
    • Dropout 生效：
      • 原始輸出中 40% 的元素被置為 0（這里 p=0.4 ，所以 5 個元素里大約 2 個被置零，對應 -0.0000 ）。
      • 未被置零的元素會被縮放：因為p=0.4，縮放系數是1/(1-0.4) ≈ 1.6667 。比如：
        • 第一個元素 0.8366 × 1.6667 ≈ 1.3944（和輸出一致）；
        • 第二個元素 -0.5336 × 1.6667 ≈ -0.8893（和輸出一致）；
    • grad_fn=<MulBackward0> 表示這是由 “乘法操作（縮放）” 產生的張量，依然支持自動求導；

• 從結果能直觀看到：

  • Dropout 隨機讓部分輸出失效（置零），強制網絡不依賴特定神經元；
  • 縮放操作保證了 “失活前后的期望一致”（比如原始輸出的平均值，和失活后縮放的平均值近似），不破壞數值分布。

4.3 批量歸一化（BN層）

• 批量歸一化（Batch Normalization，簡稱 BN 層） 的核心原理，用來解決“內部協變量偏移”問題，讓模型訓練更穩定、更快；

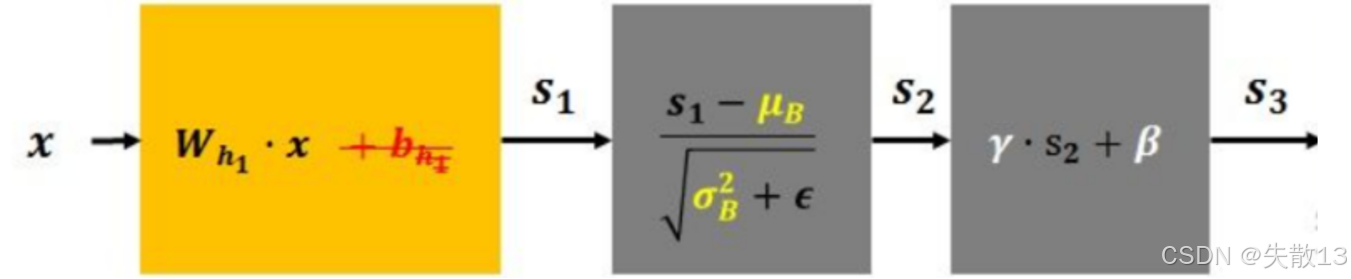
• 流程：

  

  • 線性變換。輸入 x 先經過全連接層（或卷積層）：s? = W·x + b 。這一步是神經網絡的常規操作，沒 BN 時，s? 的分布會因為參數更新不斷變化，給訓練帶來麻煩；

• 標準化。對 s? 做“標準化”，公式：
  $$s_2=\frac{s_1?{\mu }_B}{\sqrt{{\sigma }_B^2+?}}$$

  • ${\mu }_B$是 當前 batch 數據的均值，${\sigma }_B^2$是 當前 batch 數據的方差；

  • 減均值、除標準差，讓 s? 變成 均值為 0、方差為 1 的分布；

  • $\epsilon$（比如 1e-5）是為了避免分母為 0（數值穩定性）；

  • 這一步的核心：強行讓數據分布更穩定，緩解“隨著訓練，每層輸入分布總變（內部協變量偏移）”的問題，讓后續訓練更順暢；

  • 重構變換。對標準化后的 s? 做“縮放 + 平移”，公式：
    $$s_3=\gamma ?s_2+\beta$$

    • $\gamma$（縮放系數）和$\beta$（平移系數）是 可學習的參數（模型自己調）；
    • 作用：標準化會“抹掉”數據原本的分布特征，這一步讓模型有能力恢復對當前任務有用的分布（比如不想讓數據嚴格均值 0、方差 1 時，用$\gamma$和$\beta$調整）；

• 完整公式：
  $$f(x)=\lambda ?\frac{x?\text{E}(x)}{\sqrt{\text{Var}(x)}+?}+\beta$$

  • $E(x)$就是${\mu }_B$（batch 均值），$Var(x)$就是${\sigma }_B^2$（batch 方差）；

  • 先標準化（減均值除方差），再用$\gamma$和$\beta$重構 —— 和圖里的三步完全對應；

• BN層的作用：

  • 加速訓練：數據分布穩定了，模型參數更新更平滑，不用小心翼翼調學習率，收斂更快；

  • 緩解過擬合：標準化相當于給數據加了“正則”，讓模型沒那么容易學死（不過不是主要目的）；

  • 允許更大學習率：因為分布穩定，學習率可以調大，進一步加速訓練；

• 應用場景：計算機視覺領域用得多，因為 CV 任務（比如分類、檢測）的數據分布容易波動，BN 能很好地穩定訓練。

5 案例：價格分類

5.1 需求分析

• 小明創辦了一家手機公司，他不知道如何估算手機產品的價格。為了解決這個問題，他收集了多家公司的手機銷售數據。該數據為二手手機的各個性能的數據，最后根據這些性能得到4個價格區間，作為這些二手手機售出的價格區間。主要包括：

  

• 我們需要幫助小明找出手機的功能（例如：RAM等）與其售價之間的某種關系。我們可以使用機器學習的方法來解決這個問題，也可以構建一個全連接的網絡；

• 需要注意的是: 在這個問題中，我們不需要預測實際價格，而是一個價格范圍，它的范圍使用 0、1、2、3 來表示，所以該問題也是一個分類問題。接下來我們按照下面四個步驟來完成這個任務：

  • 準備訓練集數據
  • 構建要使用的模型
  • 模型訓練
  • 模型預測評估

5.2 導包

# 導包
import torch  
# TensorDataset 用于將張量數據包裝成數據集形式，方便后續數據加載
from torch.utils.data import TensorDataset  
from torch.utils.data import DataLoader  
import torch.nn as nn  
# optim模塊包含了各種優化算法（如SGD、Adam等 ），用于優化神經網絡的參數
import torch.optim as optim  
# 導入make_regression，用于生成回歸問題的數據集
from sklearn.datasets import make_regression  
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt  
import numpy as np  
import pandas as pd  
import time  

5.3 構建數據集

• 數據共有 2000 條，將其中的 1600 條數據作為訓練集，400 條數據用作測試集；

  device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")# 構建數據集
  def create_dataset():data = pd.read_csv('data/手機價格預測.csv')# 提取特征數據x：取所有行，除了最后一列的所有列（即所有特征列）x = data.iloc[:, :-1]# 提取目標數據y：取所有行，僅最后一列（即目標變量列，手機價格）y = data.iloc[:, -1]# 將特征數據x的數據類型轉換為float32，適應PyTorch模型的數值類型要求x = x.astype(np.float32)# 將目標數據y的數據類型轉換為int64（長整型），適用于分類任務的標簽類型y = y.astype(np.int64)# 將數據集劃分為訓練集和測試集（訓：測=8:2）x_train, x_valid, y_train, y_valid = train_test_split(x, y, test_size=0.2)# 構建訓練數據集：使用TensorDataset將特征和標簽的numpy數組轉換為PyTorch張量# TensorDataset是PyTorch提供的數據集包裝類，可將特征和標簽關聯起來train_dataset = TensorDataset(torch.from_numpy(x_train.values).to(device), torch.tensor(y_train.values).to(device))# 構建驗證數據集：同樣使用TensorDataset包裝測試集的特征和標簽valid_dataset = TensorDataset(torch.from_numpy(x_valid.values).to(device), torch.tensor(y_valid.values).to(device))return train_dataset, valid_dataset, x_train.shape[1], len(np.unique(y))train_dataset, valid_dataset, input_dim, class_num = create_dataset()
  print("輸入特征數：", input_dim)
  print("分類個數：", class_num)
  

  

5.4 構建分類網絡模型

• 構建全連接神經網絡來進行手機價格分類，該網絡由三個線性層來構建，使用 ReLU 激活函數；

• 網絡共有 3 個全連接層，具體信息如下：

  • 第一層：輸入維度為 20，輸出維度為 128
  • 第二層：輸入為維度為 128，輸出維度為：256
  • 第三層：輸入為維度為 256，輸出維度為：4

• 構建分類網絡模型：

  # 構建分類網絡模型
  class PhonePriceModel(nn.Module):def __init__(self, input_dim, output_dim):super(PhonePriceModel, self).__init__()# 第一層：輸入維度為 20，輸出維度為 128self.linear1 = nn.Linear(input_dim, 128)# 第二層：輸入為維度為 128，輸出維度為：256self.linear2 = nn.Linear(128, 256)# 第三層：輸入為維度為 256，輸出維度為：4self.linear3 = nn.Linear(256, output_dim)def forward(self, x):# 向前傳播x = torch.relu(self.linear1(x))x = torch.relu(self.linear2(x))output = self.linear3(x)return output# 模型實例化
  model = PhonePriceModel(input_dim, class_num).to(device)
  summary(model, input_size=(input_dim,), batch_size=16)
  

  

5.5 模型訓練

• 網絡編寫完成之后，需要編寫訓練函數；

• 所謂的訓練函數，指的是輸入數據讀取、送入網絡、計算損失、更新參數的流程，該流程較為固定；

• 使用的是多分類交叉生損失函數和 SGD 優化方法；

• 最終，將訓練好的模型持久化到磁盤中；

  # 模型訓練
  def train(train_dataset, input_dim, class_num):# 固定隨機數種子，確保訓練過程可復現（每次初始化的隨機參數相同）torch.manual_seed(0)model = PhonePriceModel(input_dim, class_num).to(device)# 定義損失函數，CrossEntropyLoss適用于多分類任務，計算預測概率分布與真實標簽的交叉熵criterion = nn.CrossEntropyLoss()# 定義優化方法，使用隨機梯度下降（SGD）優化器，學習率設置為1e-3，優化模型的參數optimizer = optim.SGD(model.parameters(), lr=1e-3)# 設置訓練輪數，即整個訓練數據集會被遍歷50次num_epoch = 50# 外層循環：遍歷每個訓練輪次for epoch_idx in range(num_epoch):# 初始化數據加載器，每次打亂數據（shuffle=True），按批次加載，每批8條數據dataloader = DataLoader(train_dataset, shuffle=True, batch_size=8)# 記錄當前輪次訓練開始時間start = time.time()# 初始化總損失，用于統計當前輪次所有批次的損失總和total_loss = 0.0# 初始化計數，用于統計批次數量（后續計算平均損失）total_num = 1# 內層循環：遍歷每個batch的數據，逐個批次訓練模型for x, y in dataloader:# 將 batch 數據送入模型，得到預測輸出。模型會根據輸入數據，通過前向傳播計算輸出結果output = model(x)# 計算當前批次的損失：將模型輸出與真實標簽代入損失函數loss = criterion(output, y)# 梯度清零：防止梯度累積影響下一次反向傳播計算，每次更新參數前要清空之前的梯度optimizer.zero_grad()# 反向傳播：根據損失值，從輸出層往輸入層反向計算每個參數的梯度loss.backward()# 參數更新：根據計算好的梯度，使用優化器更新模型的參數（如權重、偏置等）optimizer.step()# 批次計數加1，統計當前輪次處理了多少個批次total_num += 1# 將當前批次的損失值（轉為Python原生浮點數）累加到總損失中total_loss += loss.item()# 打印當前輪次的訓練信息：輪次編號、平均損失（總損失/批次數量）、訓練耗時print('epoch: %4s loss: %.2f, time: %.2fs' % (epoch_idx + 1, total_loss / total_num, time.time() - start))# 模型保存：訓練完成后，將模型的參數（state_dict）保存到指定路徑，便于后續加載復用torch.save(model.state_dict(), 'model/phone.pth') # 要提前建好 model 文件夾train(train_dataset, input_dim, class_num)
  

  

5.6 編寫評估函數

• 使用訓練好的模型，對未知的樣本的進行預測的過程，這里使用前面單獨劃分出來的驗證集來進行評估：

  def test(valid_dataset, input_dim, class_num):"""測試函數：使用訓練好的模型對驗證集數據進行預測，計算預測精度:param valid_dataset: 驗證集數據集（TensorDataset格式，包含特征和標簽）:param input_dim: 輸入特征維度:param class_num: 分類類別數量"""# 加載模型和訓練好的網絡參數# 1. 初始化模型實例，傳入輸入維度和分類數量model = PhonePriceModel(input_dim, class_num).to(device)# 2. 加載預訓練好的模型參數（注意路徑要和訓練時保存的一致#    會把訓練好的權重、偏置等參數加載到模型中，讓模型具備預測能力model.load_state_dict(torch.load('model/phone.pth'))# 構建加載器# 按批次加載驗證集數據，每批8條，測試階段不需要打亂數據（shuffle=False）dataLoader = DataLoader(valid_dataset, batch_size=8, shuffle=False)# 評估測試集# 初始化正確預測的樣本數量correct = 0  # 遍歷測試集中的每個批次數據for x, y in dataLoader:  # 將特征數據送入模型，執行前向傳播，得到輸出（模型對當前批次的預測結果，形狀一般是[batch_size, class_num] ）output = model(x)# 獲取類別結果：對輸出結果在維度1（dim=1，即類別維度）上取最大值的索引，索引對應類別y_pred = torch.argmax(output, dim=1)# 統計當前批次中預測正確的樣本數量：比較預測類別和真實類別，相同則為1，求和得到當前批次正確數，累加到totalcorrect += (y_pred == y).sum()# 求預測精度并打印# 精度 = 正確預測數 / 驗證集總樣本數 ，item()將張量轉為Python數值，按5位小數格式輸出print(f'Acc: {correct.item() / len(valid_dataset):.5f}')test(valid_dataset, input_dim, class_num)