人工智能——CNN基礎：卷積和池化

一、CNN入門介紹

1、卷積神經網絡（Convolutional Neural Network，簡稱 CNN）是一種專門為處理具有網格結構數據（如圖像、音頻）而設計的深度學習模型。

在傳統的全連接神經網絡（FNN）中，輸入的每個神經元都與下一層的所有神經元相連，這會導致參數數量隨著輸入維度的增加而急劇增長，并且無法有效利用數據的空間結構信息。（更多的只是關注了全局的特征）

而 CNN 則通過卷積層、池化層等特殊結構，大大減少了模型的參數數量，同時能夠自動提取數據中的局部特征，并且對平移、縮放等變換具有一定的不變性。。在圖像識別、目標檢測、語義分割等計算機視覺任務廣泛運用

2、卷積的思想

在之前的OpenCv的學習中，我們接觸到了很多的算子，比如Roberts算子，拉普拉斯算子等等，這些都是運用卷積的思想，對圖像操作進行邊緣提取。

可以把卷積理解為一種 “特征提取器”。想象你有一張藏寶圖（圖像），上面隱藏著各種寶藏線索（特征），但是線索分布比較雜亂。而卷積操作就像是一個帶有不同形狀 “放大鏡”（卷積核）的尋寶工具。

每個 “放大鏡” 都有自己特定的形狀和功能，比如有的專門找直線形狀的線索（檢測邊緣），有的找圓形的線索（檢測類似眼睛的部件）。當我們拿著這些 “放大鏡” 在藏寶圖上一格一格地移動（卷積核在圖像上滑動），去觀察每個小區域（感受野），就可以把對應的線索找出來，也就是提取出了圖像的局部特征

二、卷積層

1、卷積核

卷積核其實是一個小矩陣，在定義時需要考慮以下幾方面的內容：

卷積核的個數：卷積核（過濾器）的個數決定了其輸出特征矩陣的通道數。每一個卷積核對應一個通道數，也就對應一張特征圖
卷積核的值：卷積核的值是初始化好的，后續進行更新。
卷積核的大小：常見的卷積核有1×1、3×3、5×5等，一般都是奇數 × 奇數

2、卷積計算過程：

卷積的過程是將卷積核在圖像上進行滑動計算，每次滑動到一個新的位置時，卷積核和圖像進行點對點的計算，并將其求和得到一個新的值，然后將這個新的值加入到特征圖中，最終得到一個新的特征圖

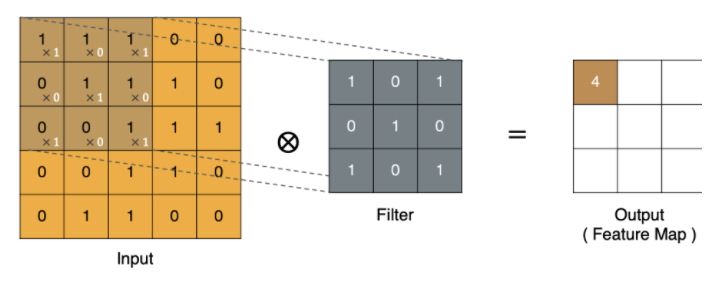
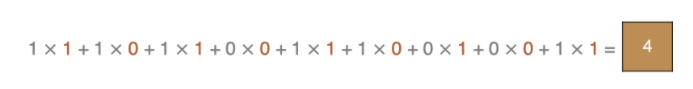
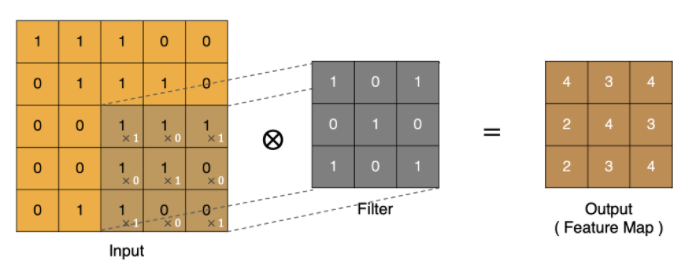
input 表示輸入的圖像
filter 表示卷積核, 也叫做濾波器
input 經過 filter 的得到輸出為最右側的圖像，該圖叫做特征圖，所有的特征圖的數量就是輸出通道數，在代碼中通常用out_channels(其實就是特征圖的數量)

代碼：了解卷積

from matplotlib import pyplot as plt
import torch.nn as nn
import os
import torchimage_path= os.path.relpath('../data/彩色.png')
img_data = plt.imread(image_path)
#shape是(高，寬，通道)(H, W, C),要轉變為(N, C, H, W)---->先轉為(C, H, W),再轉(N, C, H, W)
print(img_data.shape)img_data =torch.tensor(img_data.transpose(2,0,1)).unsqueeze(0)print(img_data.shape)#卷積層
conv = nn.Conv2d(in_channels=4,  #輸入通道數out_channels=1,  #輸出通道數(卷積核個數，對應輸出的特征個數)kernel_size=3, #卷積核大小stride=1,  #步長
)
#conv傳入的參數是(N, C, H, W)
output = conv(img_data)#輸出(N, C, H, W)
print(output.shape)#還原成圖片
out = output.squeeze(0).data.numpy()#去掉batch維度，轉成numpy數組
out = out.transpose(1,2,0)
#繪圖
plt.imshow(out)
plt.show()

正常圖片輸入的shape是(高，寬，通道)(H, W, C)，進行卷積的API：nn.Conv2d()，輸入的數據格式應該是四維的：(N, C, H, W)，在傳入img_data前需要經過轉換，先用transpose方法轉為(C, H, W)再用unqueeze在0維上升維，轉為(N, C, H, W)

Conv2d的使用
conv = nn.Conv2d(
? ? in_channels=4, ?#輸入通道數
? ? out_channels=1, ?#輸出通道數(卷積核個數，對應輸出的特征個數)
? ? kernel_size=3, #卷積核大小
? ? stride=1, ?#步長
)
????????我們需要去理解，這里的in_channels和out_channels到底是什么，在進行多層卷積神經網絡時才能正確傳入參數。
????????其中in_channels，輸入的通道數，也就是(N, C, H, W)里面的C，對于初始我們給的圖像而言，常常就是單通道（1），三通道（3），四通道（4）
????????但是經過卷積操作后，這里的out_channels輸出通道就不再是簡單的圖像上顏色對應的通道了，而是特征通道（經過每個卷積核操作后生成的特征圖個數，也就是卷積核個數）
? ? ? ? 例如：? ?
第一層卷積conv1：in_channels=1（輸入是單通道灰度圖），out_channels=16。
這意味著卷積層會創建16 個不同的 3×3 卷積核，每個卷積核專門檢測一種局部特征（如：
第 1 個卷積核：檢測水平邊緣
第 2 個卷積核：檢測垂直邊緣
第 3 個卷積核：檢測 45° 角紋理
...
第 16 個卷積核：檢測特定的斑點 / 明暗變化）
每個卷積核與輸入圖像卷積后，會輸出一張 “特征圖”（通道），16 個卷積核就得到 16 個通道，每個通道的數值表示 “該位置是否包含對應特征” 以及 “特征強度”。

3、邊緣填充

在上面的圖像中可以看出，經過卷積計算后特征圖的尺寸會比原始圖像尺寸小，這是由于在卷積過程中邊緣的像素值計算后放在卷積核中心去了，如果想要保持圖像大小不變, 可在原圖周圍添加padding來實現（邊緣填充）。

在代碼中，就是在conv = nn.Conv2d方法中加入參數padding=n，其中n表示用什么來填充，一般默認是0

4、步長
一般步長是根據圖像的大小而定，在圖像尺寸很小時，例如只有20*20，總共一行都沒多少個像素值，所以步長肯定不宜過大。當圖像比較大時，也可以適當的設置為2、3等等。需要去實驗

stride太小：重復計算較多，計算量大，訓練效率降低；
stride太大：會造成信息遺漏，無法有效提煉數據背后的特征；

5、多通道卷積計算

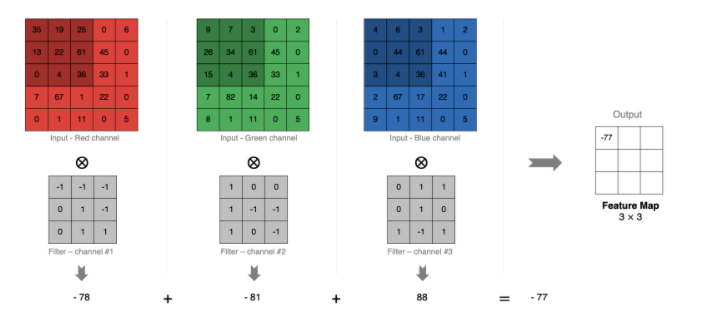
當輸入有多個通道(Channel), 例如RGB三通道, 此時要求卷積核需要有相同的通道數。
卷積核通道與對應的輸入圖像通道進行卷積。
將每個通道的卷積結果按位相加得到最終的特征圖

如圖：

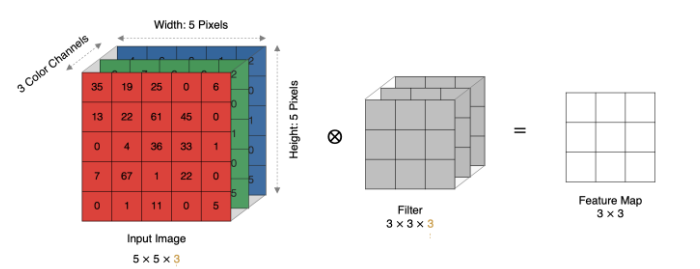
6、多卷積核計算

實際對圖像進行特征提取時, 我們需要使用多個卷積核進行特征提取，通過多個卷積核從輸入數據中提取多種類型的特征

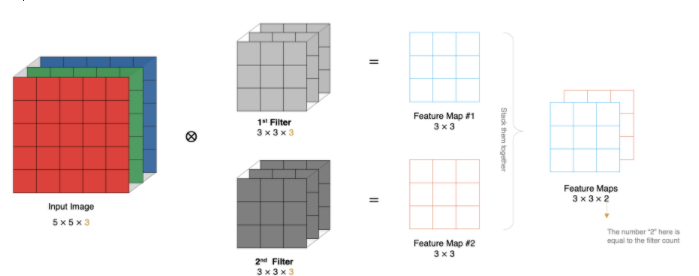
其實就是上面講Conv2d方法中提到的out_channels

用 “團隊分工” 類比多卷積核
假設你需要分析一張動物圖片：
有人負責觀察 “邊緣”（比如動物的輪廓）
有人負責觀察 “紋理”（比如毛發的粗細）
有人負責觀察 “顏色塊”（比如是否有黑白條紋）
每個人專注于一種特征，最后匯總所有觀察結果，才能全面判斷這是貓、狗還是老虎

7、特征圖大小

size: 卷積核/過濾器大小，一般會選擇為奇數，比如有 1×1, 3×3， 5×5
Padding: 零填充的方式
Stride: 步長

那計算方法如下圖所示:

輸入圖像大小: W x W
卷積核大小: F x F
Stride: S
Padding: P
輸出圖像大小: N x N

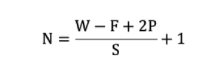
8、局部特征提取——多層多通道卷積核進行特征提取

本質是通過層級化的特征組合，從原始數據中逐步提煉出從簡單到復雜、從局部到全局的特征

用 “拼圖游戲” 類比多層特征提取
想象你在拼一幅復雜的動物拼圖：
第一層（淺層）：你先找所有帶 “直邊”“曲邊” 的拼圖塊（對應低級特征：邊緣、紋理）。
第二層（中層）：你把 “直邊 + 曲邊” 組合成 “耳朵”“爪子” 等部件（對應中級特征：局部部件）。
第三層（深層）：你把 “耳朵 + 爪子 + 身體” 組合成完整的 “貓”（對應高級特征：整體物體）。
每一層基于上一層的特征，通過多通道卷積核進行 “特征組合”，逐步構建更抽象、更有意義的表示

示例：

我們以 “RGB 圖像（3 通道）→ 3 層卷積” 為例，詳細拆解每一層的輸入、卷積核作用和輸出特征
1. 輸入層：原始圖像（物理通道）
輸入是一張?\(224 \times 224 \times 3\)?的 RGB 圖像
????????這些是最原始的像素信息，沒有經過任何特征提取
2. 第一層卷積（提取低級特征）
輸入通道：3（RGB 三通道）
卷積核設置：16 個卷積核，每個尺寸為?\(3 \times 3 \times 3\)（深度 = 輸入通道數 3，確保能覆蓋所有顏色通道）
操作邏輯：每個卷積核在輸入圖像上滑動，對 3 個顏色通道的對應區域同時計算（每個通道與卷積核的對應切片做點積，再求和），輸出 1 個特征圖。16 個卷積核共輸出 16 個通道。
輸出特征：16 個?\(222 \times 222\)?的特征圖（假設 stride=1，padding=0），每個通道對應一種低級特征：
通道 0：檢測 “水平紅色邊緣”
通道 1：檢測 “45° 綠色紋理”
通道 2：檢測 “垂直藍色邊緣”
...（16 種不同的邊緣、紋理、顏色塊特征）這些特征我們也無法確認，是計算機自行去計算，我們也不需要去搞懂到底提取了哪些特征
3. 第二層卷積（組合低級特征為中級特征）
輸入通道：16（第一層輸出的 16 種低級特征）
卷積核設置：32 個卷積核，每個尺寸為?\(3 \times 3 \times 16\)（深度 = 輸入通道數 16，能覆蓋所有低級特征）
操作邏輯：每個卷積核滑動時，會同時 “觀察” 第一層的 16 個特征通道（比如：“水平邊緣通道” 的響應 +“垂直邊緣通道” 的響應），通過權重加權求和，輸出 1 個新的特征圖。32 個卷積核輸出 32 個通道。
輸出特征：32 個?\(220 \times 220\)?的特征圖，每個通道對應中級特征
4. 第三層卷積（組合中級特征為高級特征）
輸入通道：32（第二層輸出的 32 種中級特征）
卷積核設置：64 個卷積核，每個尺寸為?\(3 \times 3 \times 32\)
操作邏輯：每個卷積核整合 32 種中級特征（比如：“角點 + 斑點 + 短線條” 的特定組合），輸出代表更復雜模式的特征圖。
輸出特征：64 個?\(218 \times 218\)?的特征圖，每個通道對應高級特征：
通道 0：“眼睛”（圓形斑點 + 周圍的邊緣輪廓）
通道 1：“車輪”（圓形紋理 + 輻射狀線條）
通道 2：“文字筆畫”（特定方向的線條組合）
...（64 種接近 “物體部件” 的特征）
多層多通道的核心機制：特征的 “層級抽象” 與 “通道協同”
層級抽象：
淺層（1-2 層）→ 低級特征（邊緣、紋理、顏色）
中層（3-4 層）→ 中級特征（角點、斑點、局部部件）
深層（5 層以上）→ 高級特征（物體部件、整體輪廓）
每一層的特征都是上一層特征的 “組合與抽象”，就像從 “字母” 到 “單詞” 再到 “句子” 的過程。
通道協同：
每個卷積核的深度 = 輸入通道數，意味著它能 “同時關注多個輸入特征”。例如，檢測 “眼睛” 的卷積核會重點關注：
輸入通道中 “圓形紋理” 的高響應區域
輸入通道中 “邊緣輪廓” 的閉合區域
輸入通道中 “膚色（特定顏色）” 的區域
這種多通道協同，讓網絡能學習 “特征之間的關聯”（比如 “圓形 + 閉合邊緣 + 膚色 = 眼睛”）。
感受野擴大：
深層卷積的 “感受野”（能影響輸出的輸入區域）比淺層大。例如：
第一層 3×3 卷積的感受野是 3×3（只看 3×3 像素）
第二層 3×3 卷積的感受野是 5×5（因為它的輸入是第一層的 3×3 區域，對應原始圖像 5×5）
第三層 3×3 卷積的感受野是 7×7
這使得深層特征能捕捉更大范圍的局部信息，為組合高級特征提供基礎。

????????什么是感受野：

感受野（Receptive Field）?是指輸出特征圖上的一個像素點，對應輸入圖像（或前層特征圖）上的區域大小
用 “望遠鏡視野” 類比感受野
想象你用望遠鏡觀察風景：
當你用低倍鏡（類似 CNN 淺層卷積）時，視野小（感受野小），只能看清眼前的細節（如一片樹葉的紋理）。
當你換高倍鏡（類似 CNN 深層卷積）時，視野大（感受野大），能看到更大范圍的場景（如整棵樹的輪廓）。
CNN 中：
淺層卷積層的感受野小，只能 “看到” 輸入圖像的局部區域（如幾個像素組成的邊緣）。
深層卷積層的感受野大，能 “看到” 輸入圖像的更大范圍（如多個局部特征組合成的部件）。
感受野的意義：
特征層級與感受野的關系：
淺層（感受野小）：捕捉邊緣、紋理等局部特征（如眼睛的輪廓、毛發的紋理）。
深層（感受野大）：捕捉部件、整體等全局特征（如人臉的整體結構、汽車的輪廓）。
例如，在識別 “貓” 的任務中：
第 1 層可能檢測 “胡須的邊緣”（感受野 3×3）。
第 3 層可能檢測 “眼睛的形狀”（感受野 7×7）。
第 5 層可能檢測 “整個貓臉”（感受野 21×21）。

多層卷積代碼示例：

from matplotlib import pyplot as plt
import torch.nn as nn
import os
import torchimage_path= os.path.relpath('../data/彩色.png')
img_data = plt.imread(image_path)
#shape是(高，寬，通道)(H, W, C),要轉變為(N, C, H, W)---->先轉為(C, H, W),再轉(N, C, H, W)
print(img_data.shape)img_data =torch.tensor(img_data.transpose(2,0,1)).unsqueeze(0)print(img_data.shape)#卷積層
#進入時的形狀：(1,4,501,500)
conv1 = nn.Conv2d(in_channels=4,#輸入通道數（N，C, H, W）out_channels=16,kernel_size=3,stride=1,
)
#conv1輸出的形狀:(1,16,499,498)conv2 = nn.Conv2d(in_channels=16,out_channels=32,kernel_size=3,stride=1,
)
#conv2輸出的形狀:(1,32,497,496)conv3 = nn.Conv2d(in_channels=32,out_channels=1,kernel_size=3,stride=1,
)
#conv3輸出的形狀:(1,1,495,494)#conv傳入的參數是(N, C, H, W)
output = conv1(img_data)#輸出(N, C, H, W)
output = conv2(output)
output = conv3(output)
# print(output.shape)#還原成圖片
out = output.squeeze(0).data.numpy()#去掉batch維度，轉成numpy數組
out = out.transpose(1,2,0)
#繪圖
plt.imshow(out)
plt.show()

三、池化層

1、池化層的概述

池化層的核心思想是“下采樣”，通過對卷積層輸出的特征圖進行局部區域的聚合操作（如取最大值、平均值），在保留關鍵特征的同時，降低特征圖的尺寸和數據量。

可以把池化層類比為 “信息壓縮器”：卷積層提取的特征圖往往包含冗余信息（比如相鄰像素的特征響應很相似），池化層就像給特征圖 “降分辨率”，只保留每個局部區域中最關鍵的信息（如最強響應、平均響應）

常見的池化方式有兩種：

最大池化（Max Pooling）：取局部區域的最大值（最常用）。
平均池化（Average Pooling）：取局部區域的平均值。

2、池化層的計算：

池化的計算邏輯與卷積類似：用一個固定大小的 “池化窗口” 在特征圖上按指定步長滑動，對窗口內的元素進行聚合操作，生成下采樣后的特征圖

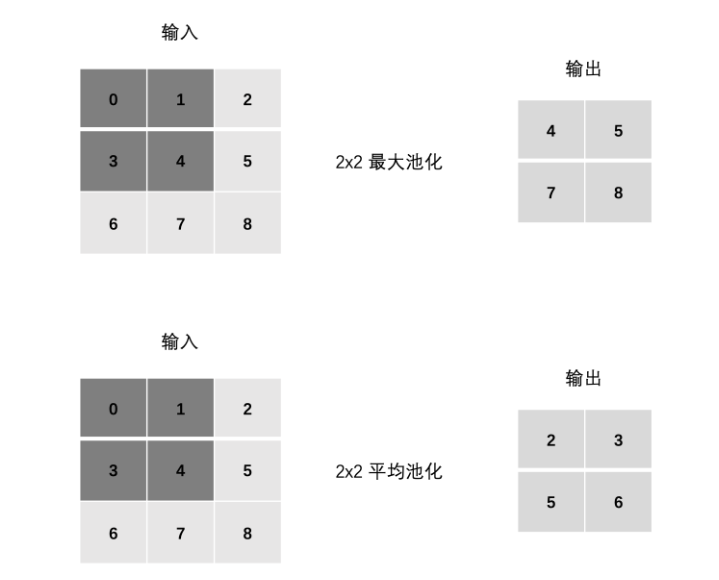
和卷積一樣也有步長Stride、Padding

另外注意：在處理多通道輸入數據時，池化層對每個輸入通道分別池化，而不是像卷積層那樣將各個通道的輸入相加。這意味著池化層的輸出和輸入的通道數是相等。

3、池化層的作用

池化操作的優勢有：

通過降低特征圖的尺寸，池化層能夠減少計算量，從而提升模型的運行效率。
池化操作可以帶來特征的平移、旋轉等不變性，這有助于提高模型對輸入數據的魯棒性。
池化層通常是非線性操作，例如最大值池化，這樣可以增強網絡的表達能力，進一步提升模型的性能。

但是池化也有缺點：

池化操作會丟失一些信息，這是它最大的缺點；

import torch
import torch.nn as nndef test01():#設置隨機種子input_map = torch.randn(1, 1, 7, 7)print(input_map)print("-"* 50)pool1 = nn.MaxPool2d(kernel_size=2,stride=1,return_indices=True#是否返回索引)output,indices = pool1(input_map)print(output,indices)print("-"*50)def test02():input_map = torch.randn(1, 1, 7, 7)pool1 = nn.AvgPool2d(kernel_size=2,stride=1,)output = pool1(input_map)print(output.shape)def test03():input_map = torch.randn(1, 1, 7, 7)pool1 = nn.AdaptiveMaxPool2d(output_size=(3,3))if __name__ == '__main__':test01()test02()

運行結果：

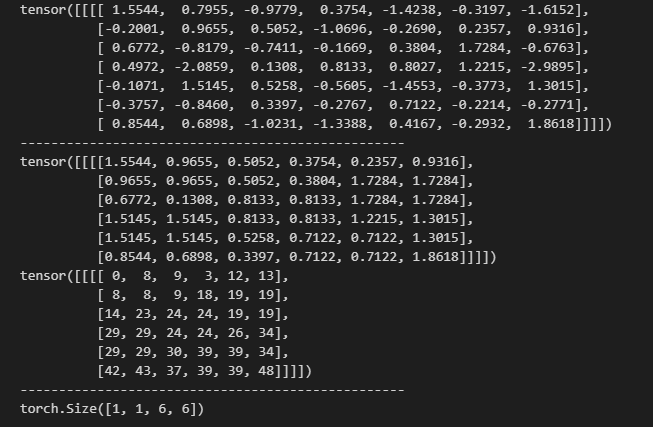
對于最大值池化。其返回值有兩個：output,indices

1.?`output`（輸出特征圖）

池化操作后的結果，即每個池化窗口中選出的最大值（對于最大池化）或平均值（對于平均池化）

2.?`indices`（索引）

在最大池化中，記錄每個池化窗口中最大值在原特征圖中的位置索引

四、自定義網絡

思路：

1、自定義網絡就是寫一個模型的類，首先定義一個類繼承于父類nn.Module

2、進行卷積操作，提取特征。定義三層卷積層，每一層進行一次池化和激活（經過池化后要算清楚輸出的圖像尺寸變化）

3、進行全連接，計算經過卷積池化操作后，總的像素點。這是全連接層特征的輸入值

4、前向傳播

5、調用模型

import torch
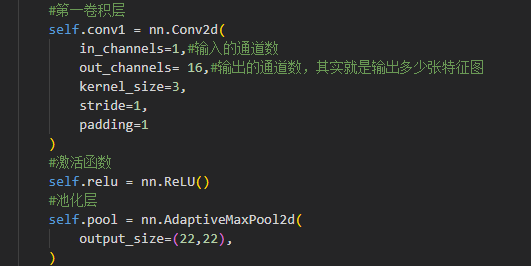
import torch.nn as nnclass MyModel(nn.Module):def __init__(self):super(MyModel, self).__init__()#第一卷積層self.conv1 = nn.Conv2d(in_channels=1,#輸入的通道數out_channels= 16,#輸出的通道數，其實就是輸出多少張特征圖kernel_size=3,stride=1,padding=1)#激活函數self.relu = nn.ReLU()#池化層self.pool = nn.AdaptiveMaxPool2d(output_size=(22,22),)#第二卷積層self.conv2 = nn.Conv2d(in_channels=16,out_channels=32,kernel_size=3,stride=1,padding=1)self.pool2 = nn.AdaptiveMaxPool2d(output_size=(16,16),)#全連接層(要判斷輸入特征就是計算像素點)self.fc1 = nn.Linear(in_features=32*16*16,out_features=10  #輸出類別數)def forward(self, x):#x(1,16,26,26)x =self.conv1(x)#x(1,16,22,22)x = self.pool(x)#x(1,32,20,20)x = self.conv2(x)#x(1,32,16,16)x = self.pool2(x)out = self.fc1(x.view(-1,x.size(1)*x.size(2)*x.size(3)))return outif __name__ == '__main__':input_data = torch.randn(1, 1, 28, 28)model = MyModel()output = model(input_data)print(output.shape)

代碼講解：

此處的out_channels前面已經講過，就是卷積核的個數，經過卷積后輸出多少張特征圖
單純的卷積后，函數也還是線性關系，所以i需要激活函數
選用自適應池化
第一步經過卷積后，圖像的尺寸變成了（原圖像大小是28*28）26*26。
經過池化后，圖像的特征減少（也就是像素減少），尺寸就變成了22*22
第二層卷積與第一層類似
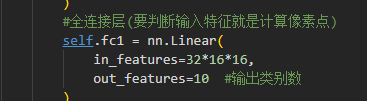
全連接層，用nn.Linear，其中輸入的特征值，其實就是經過卷積池化后，此時圖像的像素值（通道數*高*寬）
而輸出特征呢？因為我們目標是做10分類，所以最后訓練出來輸出的特征值就應該是10個類別
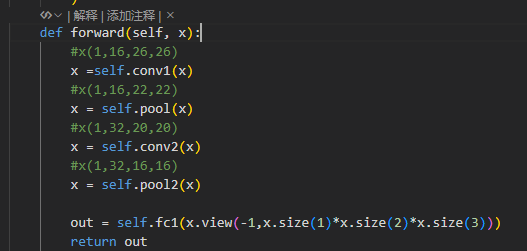
前向傳播，每次卷積和池化后，其x的形狀會發生改變，追蹤每次的改變。
為什么這么做：因為卷積神經網絡里，conv（卷積）、pool（池化）層輸出的是?4 維張量?(N, C, H, W)?（N?批大小、C?通道、H?高、W?寬），但全連接層（nn.Linear?）要求輸入是?2 維張量?(N, feature_num)?（feature_num?是一維特征數量）。所以必須用?view?把?(N, C, H, W)?轉成?(N, C*H*W)?，才能讓全連接層處理
-1?的含義：
讓 PyTorch 自動計算該維度的大小。比如?x.view(-1, A*B*C)?，-1?所在維度會被自動填充為?總元素數 / (A*B*C)?，保證元素總數不變。
具體到代碼：
假設卷積、池化后，x?的形狀是?(N, C, H, W)?（N?是 batch 數、C?是通道數、H?高、W?寬）。
執行?x.view(-1, x.size(1)*x.size(2)*x.size(3))?后：
第一個維度填?-1?，PyTorch 會自動算出是?N（因為總元素數是?N*C*H*W?，第二個維度是?C*H*W?，所以?N = 總元素數 / (C*H*W)?）。
第二個維度是?C*H*W?，把每個樣本的?(C, H, W)?三維特征圖，壓成?長度為?C*H*W?的一維向量?。
舉個實際例子：
如果?x?是?(2, 16, 22, 22)?（2 個樣本、16 通道、22 高、22 寬），執行?x.view(-1, 16*22*22)?：
第一個維度自動算成?2（總元素數?2*16*22*22 = 15488?，16*22*22=7744?，15488 / 7744=2?）。
第二個維度是?7744?，最終形狀變成?(2, 7744)?