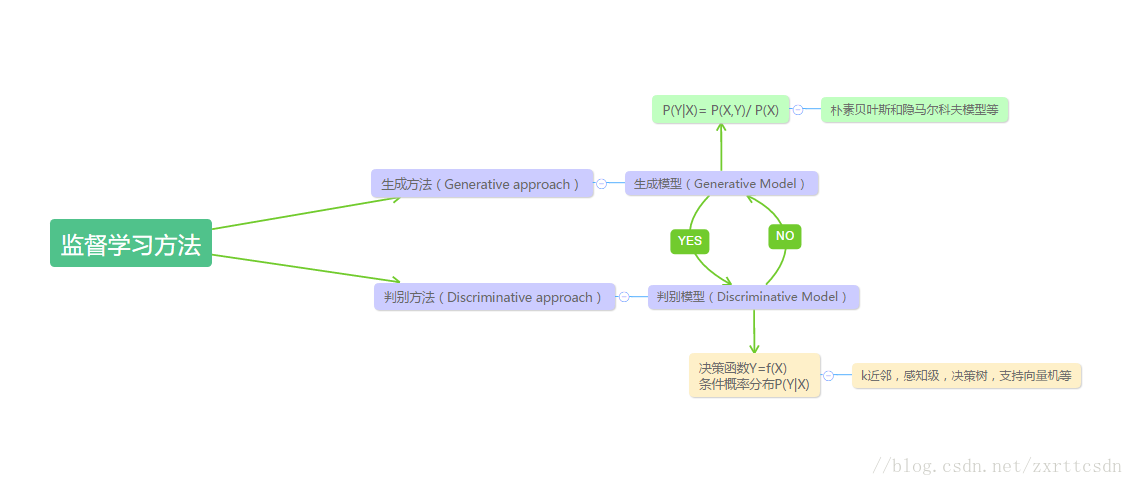
生成算法嘗試去找這個數據到底是怎么生成的(產生的),然后再對一個信號進行分類。基于你的生成假設,哪個類別最有可能產生這個信號,這個信號就屬于那個類別。
判別模型不關心數據是怎么生成的,它只關心信號之間的差別,然后模型學習到差別之后簡單地對給定的一個信號進行分類。
?
在機器學習中,無監督學習(Unsupervised learning)最典型的就是聚類,事先不知道樣本的類別,通過某種辦法,把相似的樣本放在一起歸位一類;而監督學習(Supervised learning)就是有訓練樣本,帶有屬性標簽,也可以理解成樣本有輸入有輸出,意味著輸入和輸出之間有一個關系,監督學習算法就是要發現和總結這種“關系”。
以下是一些常用的監督型學習方法:
一. K-近鄰算法(k-Nearest Neighbors,KNN)
算法的步驟為:
(1)計算測試數據與各個訓練數據之間的距離;
(2)按照距離的遞增關系進行排序;
(3)選取距離最小的K個點;
(4)確定前K個點所在類別的出現頻率;
(5)返回前K個點中出現頻率最高的類別作為測試數據的預測分類。
二. 決策樹(Decision Trees)
決策樹是一個樹結構(可以是二叉樹或非二叉樹)。其每個非葉節點表示一個特征屬性上的測試,每個分支代表這個特征屬性在某個值域上的輸出,而每個葉節點存放一個類別。使用決策樹進行決策的過程就是從根節點開始,測試待分類項中相應的特征屬性,并按照其值選擇輸出分支,直到到達葉子節點,將葉子節點存放的類別作為決策結果。
相比貝葉斯算法,決策樹的優勢在于構造過程不需要任何領域知識或參數設置。
構造決策樹的關鍵步驟是分裂屬性。所謂分裂屬性就是在某個節點處按照某一特征屬性的不同劃分構造不同的分支,其目標是讓各個分裂子集盡可能地“純”。盡可能“純”就是盡量讓一個分裂子集中待分類項屬于同一類別。分裂屬性分為三種不同的情況:
1、屬性是離散值且不要求生成二叉決策樹。此時用屬性的每一個劃分作為一個分支。
2、屬性是離散值且要求生成二叉決策樹。此時使用屬性劃分的一個子集進行測試,按照“屬于此子集”和“不屬于此子集”分成兩個分支。
3、屬性是連續值。此時確定一個值作為分裂點split_point,按照 >split_point 和 <=split_point 生成兩個分支。
構造決策樹的關鍵性內容是進行屬性選擇度量,屬性選擇度量算法有很多,這里介紹ID3和C4.5兩種常用算法。
(1) ID3算法
從信息論知識中我們直到,期望信息越小,信息增益越大,從而純度越高。所以ID3算法的核心思想就是以信息增益度量屬性選擇,選擇分裂后信息增益最大的屬性進行分裂。
熵(entropy)是描述信息不確定性(雜亂程度)的一個值。設S是用類別對訓練元組進行的劃分,那么S的信息熵的定義如下:
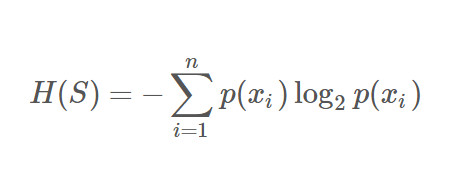
其中,n是類別的數目,p(xi)表示選擇xi類別的概率(可用類別數量除以總數量估計)。
現在我們假設將S按屬性A進行劃分,則S的條件信息熵(也就是A對S劃分的期望信息)為:
?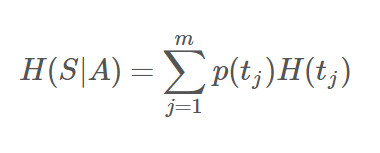
其中,屬性A擁有m個類別(例如,屬性A是體重,有輕、中、重三個選項,那么m=3),p(tj)表示類別tj(屬性A中所有具有第j個特性的所有數據)的數量與S總數量的比值,H(tj)表示子類別tj的熵,即S中擁有屬性tj的子元組劃分的熵。
而信息增益(Information gain)即為兩者的差值:
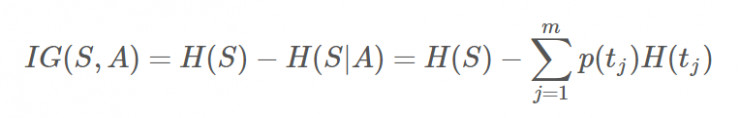
ID3算法就是在每次需要分裂時,計算每個屬性的增益率,然后選擇增益率最大的屬性進行分裂。如此迭代,直至結束。這里有一個ID3算法的實例過程。
對于特征屬性為離散值,可以直接使用ID3算法進行劃分。對于特征屬性為連續值,可以如此使用ID3算法:
先將D中元素按照特征屬性排序,則每兩個相鄰元素的中間點可以看做潛在分裂點,從第一個潛在分裂點開始,分裂D并計算兩個集合的期望信息,具有最小期望信息的點稱為這個屬性的最佳分裂點,其信息期望作為此屬性的信息期望。
(2) C4.5算法
ID3算法存在一個問題,就是偏向于多值屬性,例如,如果存在唯一標識屬性ID,則ID3會選擇它作為分裂屬性,這樣雖然使得劃分充分純凈,但這種劃分對分類幾乎毫無用處。ID3的后繼算法C4.5使用增益率(gain ratio)的信息增益擴充,試圖克服這個偏倚。嚴格上說C4.5是ID3的一個改進算法。
C4.5首先定義了分裂信息(Split Information):
??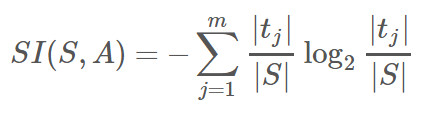
其中各符號意義與ID3算法相同,然后,增益率(Gain Ratio)被定義為:
??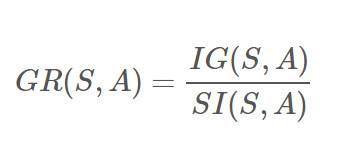
C4.5選擇具有最大增益率的屬性作為分裂屬性(連續屬性要用增益率離散化)。C4.5算法有如下優點:產生的分類規則易于理解,準確率較高。其缺點是:在構造樹的過程中,需要對數據集進行多次的順序掃描和排序,因而導致算法的低效。此外,C4.5只適合于能夠駐留于內存的數據集,當訓練集大得無法在內存容納時程序無法運行。
?
在決策樹構造過程中,如果所有屬性都作為分裂屬性用光了,但有的子集還不是純凈集,即集合內的元素不屬于同一類別。在這種情況下,由于沒有更多信息可以使用了,一般對這些子集進行“多數表決”,即使用此子集中出現次數最多的類別作為此節點類別,然后將此節點作為葉子節點。
在實際構造決策樹時,通常要進行剪枝,這是為了處理由于數據中的噪聲和離群點導致的過分擬合問題。剪枝有兩種:先剪枝——在構造過程中,當某個節點滿足剪枝條件,則直接停止此分支的構造;后剪枝——先構造完成完整的決策樹,再通過某些條件遍歷樹進行剪枝。悲觀錯誤剪枝PEP算法是一種常見的事后剪枝策略。
三. 樸素貝葉斯(Naive Bayesian)
貝葉斯分類是一系列分類算法的總稱,這類算法均以貝葉斯定理為基礎,故統稱為貝葉斯分類。樸素貝葉斯算法(Naive Bayesian) 是其中應用最為廣泛的分類算法之一。樸素貝葉斯分類器基于一個簡單的假定:給定目標值時屬性之間相互條件獨立。樸素貝葉斯的基本思想是對于給出的待分類項,求解在此項出現的條件下各個類別出現的概率,哪個最大,就認為此待分類項屬于哪個類別。
首先給出條件概率的定義,P(A | B)表示事件A在B發生下的條件概率,其公式為:
??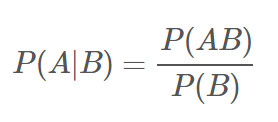
貝葉斯定理用來描述兩個條件概率之間的關系,貝葉斯定理公式為:
??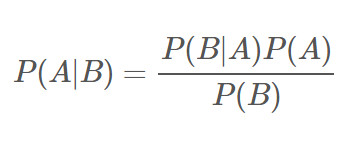
樸素貝葉斯分類算法的具體步驟如下:
(1)設x = {a1,a2,...,am}為一個待分類項,a1,a2,...,am為x的m個特征屬性;
(2)設有類別集合C = {y1,y2,...,yn},即共有n個類別;
(3)依次計算x屬于各項分類的條件概率,即計算P(y1 | x),P(y2 | x),… ,P(yn | x):

注意,算法的下一步驟是對比這些結果的大小,由于各項分母都是P(x),所以分母不用計算。分子部分中P(yn)和P(ai | yn)都是通過樣本集統計而得,其中P(yn)的值為樣本集中屬于yn類的數量與樣本總數量之比,P(ai∥yn)的值為yn類中滿足屬性ai的數量與yn類下樣本總數量之比。
這樣的計算方式符合特征屬性是離散值的情況,如果特征屬性是連續值時,通常假定其值服從高斯分布(也稱正態分布),高斯分布即:
? ?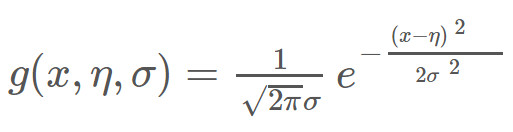
那么P(ai | yn)的值為:
??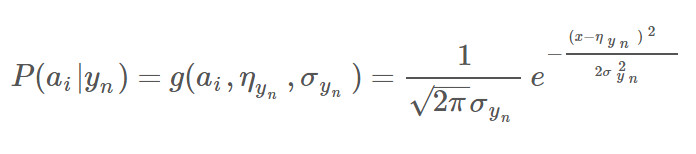
其中,ηyn 和 σyn 分別為訓練樣本yn類別中ai屬性項對應的高斯分布的均值和標準差。
對于P(a | y)=0的情況,當某個類別下某個屬性項劃分沒有出現時,就是產生這種現象,這會令分類器質量大大降低。因此引入Laplace校準,對每個類別下所有屬性劃分的計數加1,這樣如果訓練樣本集數量充分大時,并不會對結果產生影響,也避免了乘積為0的情況。
(4)比較(3)中所有條件概率的大小,最大的即為預測分類結果,即:
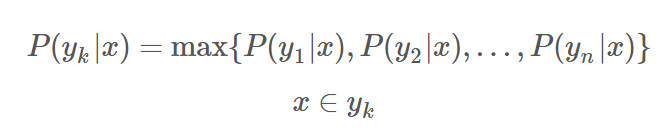
四. 邏輯回歸(Logistic Regression)
我們知道,線性回歸就是根據已知數據集求一線性函數,使其盡可能擬合數據,讓損失函數最小,常用的線性回歸最優法有最小二乘法和梯度下降法。而邏輯回歸是一種非線性回歸模型,相比于線性回歸,它多了一個sigmoid函數(或稱為Logistic函數)。邏輯回歸是一種分類算法,主要用于二分類問題。
對于線性回歸,損失函數是歐式距離指標,但這樣的Cost Function對于邏輯回歸是不可行的,因為在邏輯回歸中平方差損失函數是非凸,我們需要其他形式的Cost Function來保證邏輯回歸的成本函數是凸函數。我們選擇交叉熵損失函數。
與線性回歸相似,可以采用梯度下降法尋優,也可以采用其他方法。
?
題外話,對數似然函數與交叉熵損失函數的聯系:
對數似然函數:
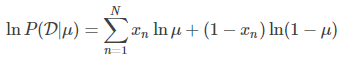
交叉熵損失函數:
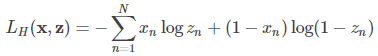
x 表示原始信號,z 表示重構信號。(損失函數的目標是最小化,似然函數的目標則是最大化,二者僅相差一個負號)。
?
https://blog.csdn.net/zxrttcsdn/article/details/79641054
https://www.leiphone.com/news/201704/w6SbD8XGrvQ9IQTB.html
https://www.cnblogs.com/leoo2sk/archive/2010/09/19/decision-tree.html
https://blog.csdn.net/lanchunhui/article/details/75433608





![昨天,我的大學學習[2]](http://pic.xiahunao.cn/昨天,我的大學學習[2])













