歸并排序不使用遞歸

• 使用一個變量，使其按照1、2、4、8遞增，控制左右兩邊1個元素、2個元素、4個元素等元素的合并

完全二叉樹

• 完全二叉樹 要不全是滿的，要不葉子節點出現在最后一層，只要出現了葉子節點，后面的都是葉子節點
• 完全二叉樹可以用數組下標從0-7來表示，依據以下公式計算左節點、右節點和父節點
• 對于任意節點 i?
• 左節點? 2*i+1
• 右節點? 2*i+2
• 父節點? (i-1)/2

堆

堆（完全二叉樹）

大根堆

• 在完全二叉樹上，每一個子樹的最大值都是頭節點

小根堆

• 在完全二叉樹上，每一個子樹的最小值都是頭節點

堆的插入和刪除操作是O(logn),構建堆的操作是O(n)

堆的存儲方式不是鏈式存儲，而是順序存儲。左孩子下標是 2*parent +1;右孩子下標是2 * parent+2

優先隊列：比如最大優先隊列，讓最大的元素出隊，即使最大元素不在隊頭，他仍然是第一個出隊，因為它優先級最高。優先隊列的底層是使用大根堆來實現的。每一次入隊操作就是堆的插入操作，每一次出隊操作就是刪除堆頂點

因為二叉堆的上浮和下沉的時間復雜度都是O(logn),因此優先隊列的入隊和出隊的時間復雜度也是O(logn)

例子

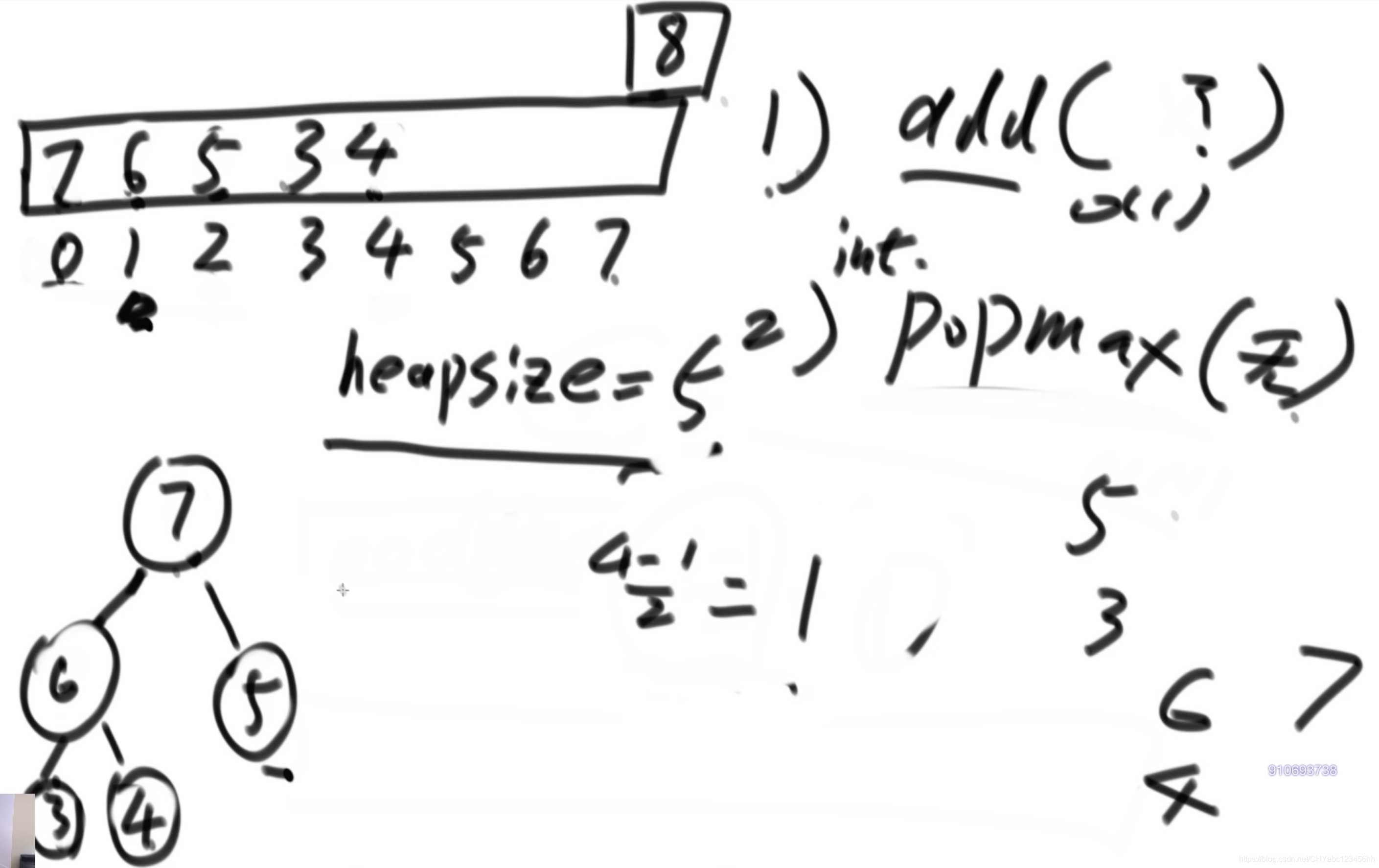
• 加入元素：數組下標從0到7，按照輸入的順序加入到數組中，沒加入一個數組根據公式（i-1）/ 2來判定，他的父節點的位置，然后與父節點做比較，如果大于父節點則和父節點的位置交換。每加入一個元素，那么heapsize+1。heapsize用于指定堆的大小。
• 返回最大值：將大根堆的最頂端和最末尾的元素相互交換，然后將heapsize-1，返回最頂端的數值。末尾元素移到最頂端之后，需要找到它的左右兩個孩子節點，做比較，如果有比它還大的孩子節點就進行交換。依此類推。
• 數組擴容：如果原始只分配一個字節，動態加入元素，進行數組擴容。那么需要log（N）次數的擴容，最后需要拷貝N個數到擴容完成后的數組中；因此代價是 N*log（N），如果取平均，最后代價是log（N）

完整代碼

• heapsort方法適用于 將元素插入數組，一個一個往里面放
• heapify 適用于如果將元素彈出的時候，將最小的元素放在頂端，看其是否下降
• 還不是很了解 這個代碼的含義

package class02;import java.util.Arrays;
import java.util.PriorityQueue;public class Code03_HeapSort {public static void heapSort(int[] arr) {if (arr == null || arr.length < 2) {return;}for (int i = 0; i < arr.length; i++) { // O(N)heapInsert(arr, i); // O(logN)}// for(int i = arr.length -1; i >=0; i--) {// heapify(arr, i, arr.length);// }int heapSize = arr.length;swap(arr, 0, --heapSize);while (heapSize > 0) { // O(N)heapify(arr, 0, heapSize); // O(logN)swap(arr, 0, --heapSize); // O(1)}}// arr[0 ... index-1]已經是堆了某個數現在處在index位置，往上繼續移動public static void heapInsert(int[] arr, int index) {while (arr[index] > arr[(index - 1) / 2]) {swap(arr, index, (index - 1) / 2);index = (index - 1) / 2;}}// 某個數在index位置，能否往下移動public static void heapify(int[] arr, int index, int heapSize) {int left = index * 2 + 1; // 左孩子的下標while (left < heapSize) { // 下方還有孩子的時候// 兩個孩子中，誰的值大，把下標給largestint largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;// 父和較大的孩子之間，誰的值大，把下標給largestlargest = arr[largest] > arr[index] ? largest : index;if (largest == index) {break;}swap(arr, largest, index);index = largest;left = index * 2 + 1;}}public static void swap(int[] arr, int i, int j) {int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;}// for testpublic static void comparator(int[] arr) {Arrays.sort(arr);}// for testpublic static int[] generateRandomArray(int maxSize, int maxValue) {int[] arr = new int[(int) ((maxSize + 1) * Math.random())];for (int i = 0; i < arr.length; i++) {arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());}return arr;}// for testpublic static int[] copyArray(int[] arr) {if (arr == null) {return null;}int[] res = new int[arr.length];for (int i = 0; i < arr.length; i++) {res[i] = arr[i];}return res;}// for testpublic static boolean isEqual(int[] arr1, int[] arr2) {if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {return false;}if (arr1 == null && arr2 == null) {return true;}if (arr1.length != arr2.length) {return false;}for (int i = 0; i < arr1.length; i++) {if (arr1[i] != arr2[i]) {return false;}}return true;}// for testpublic static void printArray(int[] arr) {if (arr == null) {return;}for (int i = 0; i < arr.length; i++) {System.out.print(arr[i] + " ");}System.out.println();}// for testpublic static void main(String[] args) {int index = -1;System.out.println(index / 2);int testTime = 500000;int maxSize = 100;int maxValue = 100;boolean succeed = true;for (int i = 0; i < testTime; i++) {int[] arr1 = generateRandomArray(maxSize, maxValue);int[] arr2 = copyArray(arr1);heapSort(arr1);comparator(arr2);if (!isEqual(arr1, arr2)) {succeed = false;break;}}System.out.println(succeed ? "Nice!" : "Fucking fucked!");int[] arr = generateRandomArray(maxSize, maxValue);printArray(arr);heapSort(arr);printArray(arr);}}

比較器的使用

• 實質：重載比較運算符
• 比較器可以應用在特殊標準的排序上
• 比較器可以應用在特殊標準的排序結構上
• 自己定義比較規則? 類似 C++運算符號重載，比如定義一個學生結構體，包含學生的名字、年齡和id；通過結構的年齡的比較，進行排序

堆排序的擴展題目

• 已知一個幾乎有序的數組，幾乎有序是指，如果將數組排好順序的話，每個元素的移動距離不超過k，并且k相對于數組來說比較小。請選擇一個合適的排序算法針對這個數據進行排序
• 思路：使用一個大小為 k+1 的內存空間，主要目的是要小根堆，先將k+1個元素放入申請的內存空間，每次放入都需要進行一次調整；此時0位置的元素是最小的元素；然后將0位置元素彈出，再將新的元素插入申請的空間，進行調整。（每彈出一個首元素，再插入一個新的元素，整體調整）?（每個數進入一次彈出一次，N*logk）
• ?

?

?