桶排序
計數排序(基于統計)
- 要求數據是有限的,和數據狀況有關,比如對于200個人統計他們的年齡分布,這個時候需要申請200個桶,因此對于輸入數據的規模有限制,如果輸入規模是不定的,空間申請就會很麻煩。
基數排序
思想
- 要求排序的數字都是十進制的數字,找到最高位的數字,對于其中不滿足位數的數字前面補0,例如【100,23,34】就需要改寫成【100,023,034】的形式。
- 準備和數字相同數目的桶(類比于先進先出的隊列),所有數字按照個位數字進桶,然后按照從左往右的次序依次往出倒數字,如果一個桶內有多個數字按照次序(隊列)倒數,再按照十位數字進桶,原理和先前類似,倒出;再按照百位數字進桶,出桶。最后的次序是從小到大的。
落地
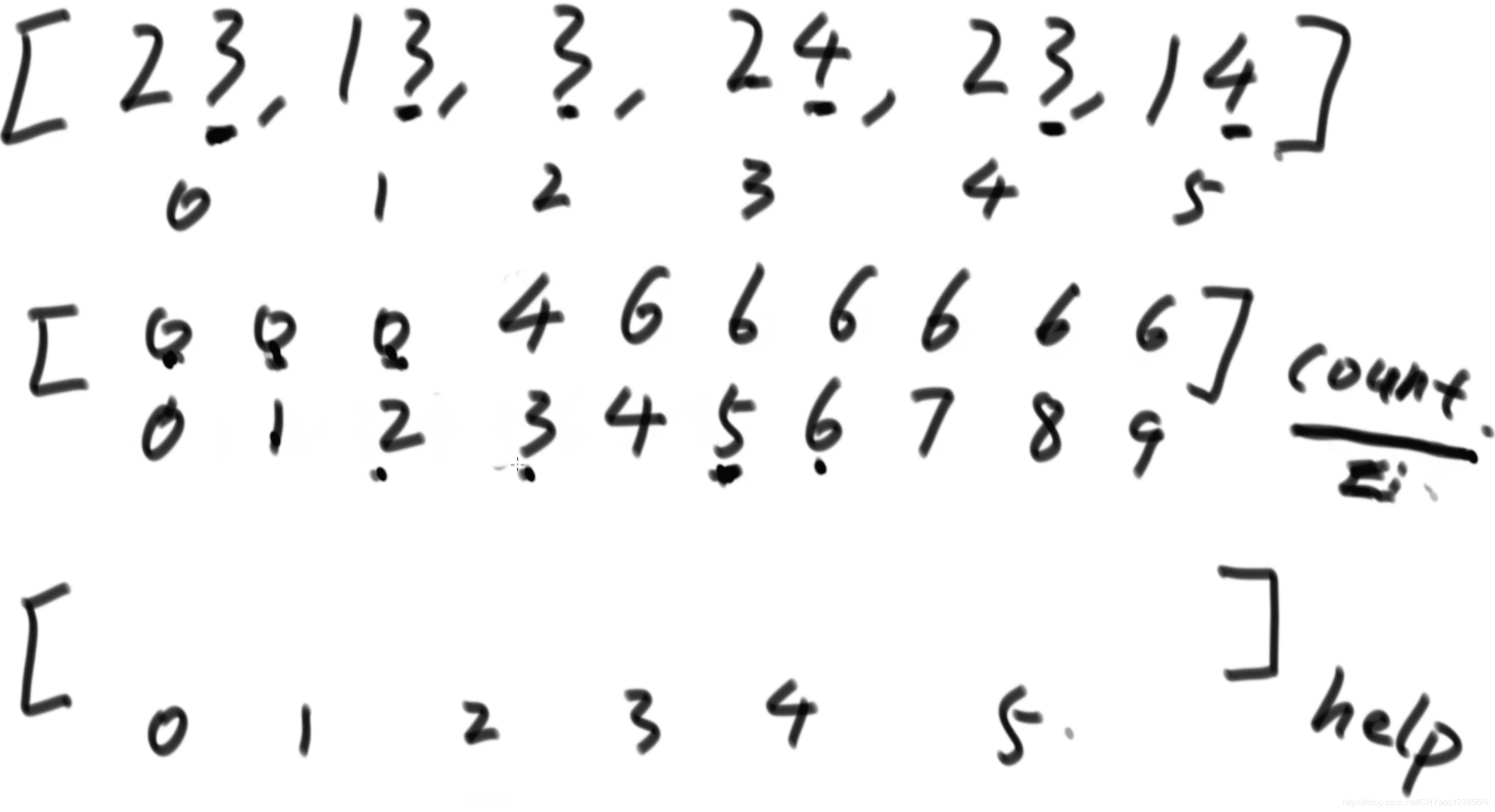
- 初始數組為【23,13,3,24,23,14】,申請兩個棧,一個為count,一個是help。count按照次序分別是【0,1,2,3,4,5,6,7,8,9】這個用于統計對應的數字的個數,比如上面這個例子的話,個位是3的個數有4個,個位是4的個數有3個。而help指定的是數組中元素的個數。此時一個6個元素,所以將help的大小設置為6。
- ?統計完對應的數字數字之后,得到的count為【0,0,0,4,2,0,0,0,0,0】,對其進行加工,對應元素的位置等于自身的值+前面的元素值。如果是0號位置就是本身,1號就是0+0,2號是0+0;3號是4+0;4號是4+0;5號是6+0;依次類推剩余元素的值都是6。經過加工后的count數組含義就是小于等于相應位置上元素的個數。比如小于等于3的有三個元素;小于等于5,6,7,8,9的有6個元素。
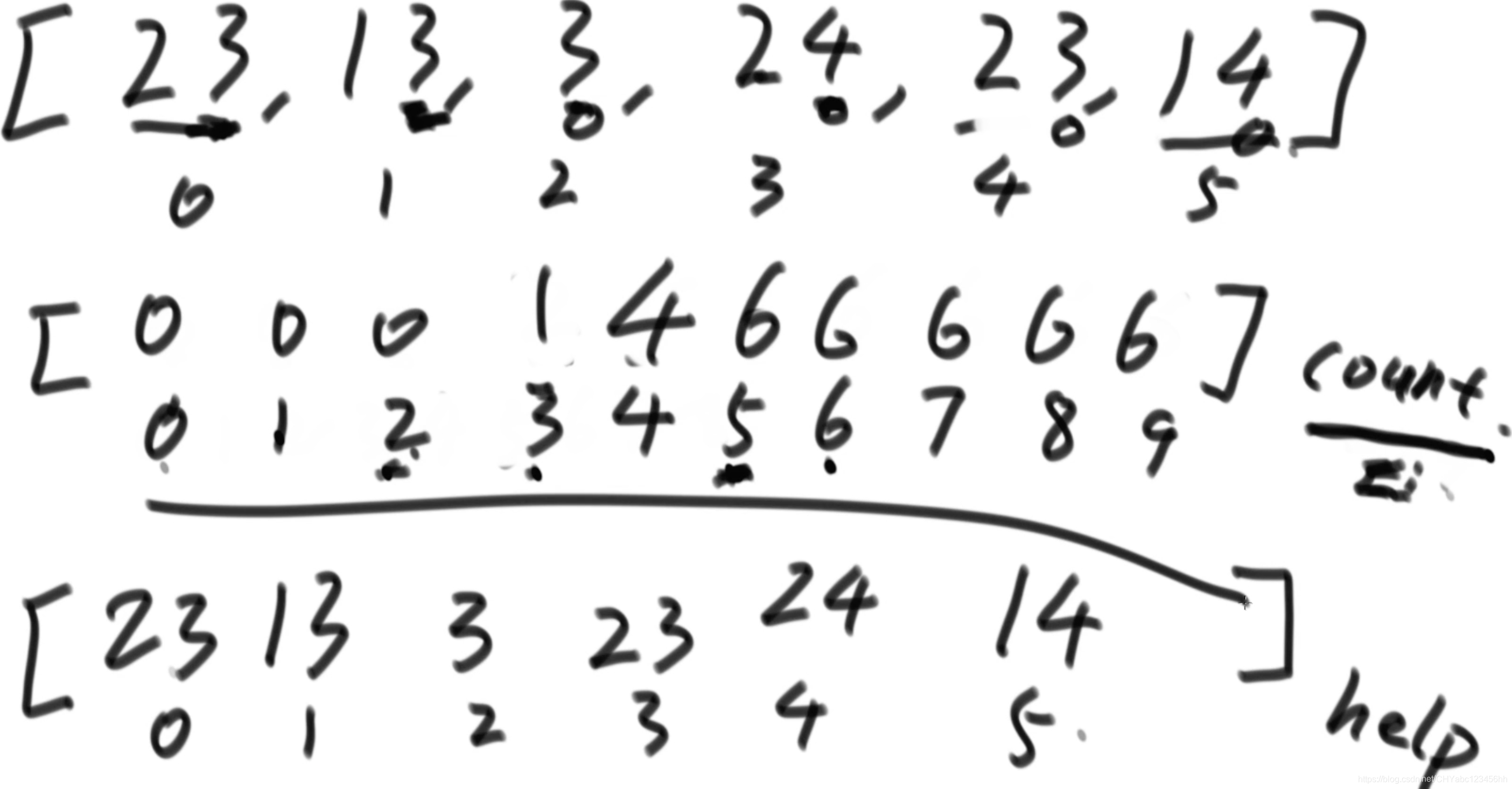
操作過程?
- 從右往左遍歷,第一個元素是14,個位數小于等于6的有6個,所以將14填寫在help的5位置上,并且將count數組中的4對應的6減1,變成5。
- 下一個元素是23,個位元素對應的是3,查詢count數組,小于等于3的元素有四個,因此將23填寫在help數組的3號位置,count中3號位置的4減1;
- 下一個元素是24,?個位元素對應的是4,查詢count數組,小于等于4的元素有5個,因此將24填寫在help數組的4號位置,count中4號位置的5減1;
- 下一個元素是3,?個位元素對應的是3,查詢count數組,小于等于3的元素有3個,因此將3填寫在help數組的2號位置,count中3號位置的3減1;
- 下一個元素是13,?個位元素對應的是3,查詢count數組,小于等于3的元素有2個,因此將3填寫在help數組的1號位置,count中3號位置的2減1;
- 下一個元素是23,?個位元素對應的是3,查詢count數組,小于等于3的元素有1個,因此將3填寫在help數組的0號位置,count中3號位置的1減1;
完整代碼
package class03;import java.util.Arrays;public class Code02_RadixSort {// only for no-negative valuepublic static void radixSort(int[] arr) {if (arr == null || arr.length < 2) {return;}radixSort(arr, 0, arr.length - 1, maxbits(arr));}public static int maxbits(int[] arr) {int max = Integer.MIN_VALUE;for (int i = 0; i < arr.length; i++) {max = Math.max(max, arr[i]);}int res = 0;while (max != 0) {res++;max /= 10;}return res;}// arr[begin..end]排序public static void radixSort(int[] arr, int L, int R, int digit) {final int radix = 10;int i = 0, j = 0;// 有多少個數準備多少個輔助空間int[] bucket = new int[R - L + 1];for (int d = 1; d <= digit; d++) { // 有多少位就進出幾次// 10個空間// count[0] 當前位(d位)是0的數字有多少個// count[1] 當前位(d位)是(0和1)的數字有多少個// count[2] 當前位(d位)是(0、1和2)的數字有多少個// count[i] 當前位(d位)是(0~i)的數字有多少個int[] count = new int[radix]; // count[0..9]for (i = L; i <= R; i++) {j = getDigit(arr[i], d);count[j]++;}for (i = 1; i < radix; i++) {count[i] = count[i] + count[i - 1];}for (i = R; i >= L; i--) {j = getDigit(arr[i], d);bucket[count[j] - 1] = arr[i];count[j]--;}for (i = L, j = 0; i <= R; i++, j++) {arr[i] = bucket[j];}}}public static int getDigit(int x, int d) {return ((x / ((int) Math.pow(10, d - 1))) % 10);}// for testpublic static void comparator(int[] arr) {Arrays.sort(arr);}// for testpublic static int[] generateRandomArray(int maxSize, int maxValue) {int[] arr = new int[(int) ((maxSize + 1) * Math.random())];for (int i = 0; i < arr.length; i++) {arr[i] = (int) ((maxValue + 1) * Math.random());}return arr;}// for testpublic static int[] copyArray(int[] arr) {if (arr == null) {return null;}int[] res = new int[arr.length];for (int i = 0; i < arr.length; i++) {res[i] = arr[i];}return res;}// for testpublic static boolean isEqual(int[] arr1, int[] arr2) {if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {return false;}if (arr1 == null && arr2 == null) {return true;}if (arr1.length != arr2.length) {return false;}for (int i = 0; i < arr1.length; i++) {if (arr1[i] != arr2[i]) {return false;}}return true;}// for testpublic static void printArray(int[] arr) {if (arr == null) {return;}for (int i = 0; i < arr.length; i++) {System.out.print(arr[i] + " ");}System.out.println();}// for testpublic static void main(String[] args) {int testTime = 500000;int maxSize = 100;int maxValue = 100000;boolean succeed = true;for (int i = 0; i < testTime; i++) {int[] arr1 = generateRandomArray(maxSize, maxValue);int[] arr2 = copyArray(arr1);radixSort(arr1);comparator(arr2);if (!isEqual(arr1, arr2)) {succeed = false;printArray(arr1);printArray(arr2);break;}}System.out.println(succeed ? "Nice!" : "Fucking fucked!");int[] arr = generateRandomArray(maxSize, maxValue);printArray(arr);radixSort(arr);printArray(arr);}}
穩定性
- ?相同元素排序保證先后順序
- 同樣數值的個體之間,如果不因為排序而改變相對次序,這個排序就是有穩定性的,否則則沒有
- 基于比較的排序,一般都是不穩定的;基數排序(按照個位、十位、百位上的元素的大小進行相對次序的排列)和計數排序(統計相同數值的元素出現的次數,押入對應的元素組成的數據棧,利用棧先入后出的特性,保持元素的相對次序,參考上文統計0-200員工年齡分布問題)是穩定的
- 不具備穩定性的排序:選擇排序、快速排序 和 堆排序
- 具備穩定性的排序 :冒泡排序、插入排序 、歸并排序 、一切桶排序思想下的排序(計數排序和基數排序)
- 目前沒有 時間復雜度為O(N*logN)? 額外時間復雜度O(1)? 又穩定的排序
- 穩定性 主要體現在 非基礎類型數據的排序,比如對自定義結構體學生類型{年齡、班級},先按照年齡排序,再按照班級進行排序
分析:
- 桶排序思想下的排序都是不基于比較的排序
- 時間復雜度為O(N),額外空間負載度O(M)
- 應用范圍有限,需要樣本的數據狀況滿足桶的劃分
匯總
- 快速排序不是基于比較的排序
| ? | 時間 | 空間 | 穩定性 | 備注 |
| 選擇排序 | O(N^2) | O(1) | 不穩定 | {5,5,5,3} 3和第一個5交換,不穩定 |
| 冒泡排序 | O(N^2) | O(1) | 穩定 | ? |
| 插入排序 | O(N^2) | O(1) | 穩定 | {3,4,4,5}新插入元素4,不可以越過與其相等元素的左邊,即元素相等的話,只會排在相等區域的最后位置 |
| 歸并排序 | O(N*logN) | O(N) | 穩定 | {1,1,2,2}{1,1,2,2}左邊和右邊進行比較拼接的時候,先拷貝左邊的元素,再拷貝右邊的元素 |
| 快速排序 | O(N*logN) | O(logN) | 不穩定 | {3,4,5,6,6,6,6,6,|2,333}? 2會和第一個6進行交換,打破了相對次序 |
| 堆排序 | O(N*logN) | O(1) | 不穩定 | 樹狀結構,{5,5,5,5,6}第一個5會和6交換,不穩定 |
| 桶排序(基數/計數) | O(N) | O(M) | 穩定 | 非比較 |
- 歸并、快排、和堆排序最為關鍵;不在乎穩定性的前提小,使用快速排序最好,時間最快(實驗可知);需要穩定性的話,使用歸并排序;在乎額外空間的話,使用堆排序
常見的坑
- 歸并排序的額外空間復雜度可以變為O(1),但是會失去穩定性的優勢,詳見《歸并排序,內部緩沖法》
- 原地歸并排序,很垃圾,會將時間復雜度變成O(N^2)
- 快速排序也可以做到穩定性,但是非常難,詳見《01 stable sort》
- 所有的改進都不重要? 目前沒有 時間復雜度為O(N*logN) 額外空間復雜度為? O(1) 又穩定的排序
- 將一個數組中,所有的奇數移到數組的左邊,所有的偶數移到數組的右邊。保持相對次序不變的同時,要是時間復雜度為O(N),空間復雜度為O(1)。這個沒法做😂😂😂😂
對于排序的改進優化
- 充分利用O(N*logN)和O(N^2)的排序的各自優勢
-
數據規模很大的時候使用快速排序,當數據規模減少,數據項在60以內的時候,該換成插入排序,同時使用快速和插入兩種方法,能進一步提高效率,減少時間復雜度。
穩定性考慮
- 如果輸入的數據是基礎類型,使用快速排序;如果輸入的類型是自定義的類型,使用插入、歸并這些可以保證穩定性的排序方法
- Java里面自帶的排序算法,即array.sort,如果是常規類型,比如int的話是使用快速排序,提高速度;如果是自定義的類型,比如學生的年齡,結構體定義的字段,會使用桶排序,保證比較的穩定性。即算法看重時間復雜度 空間復雜度和穩定性(數值相等的元素排序,保證先后次序不變)
- 基礎類型按照數值傳遞,非基礎類型,比如自定義結構體按照引用傳遞,具體體現在integer這個類型,127相等,128就不等了。因為128以上就作為不同內存了,也就是按照引用比較了


)
















