牛客網?左程云老師的算法入門課
貪心算法

貪心算法的解題步驟?
例子?
題目要求
 ?解題策略
?解題策略
-
按照結束時間早的會議先安排,比如先安排【2,4】,當4結束了,所有開始時間小于4的全部淘汰,【1,7】、【3,4】,【2,8】,將【5,6】加入安排,將【7,10】加入安排
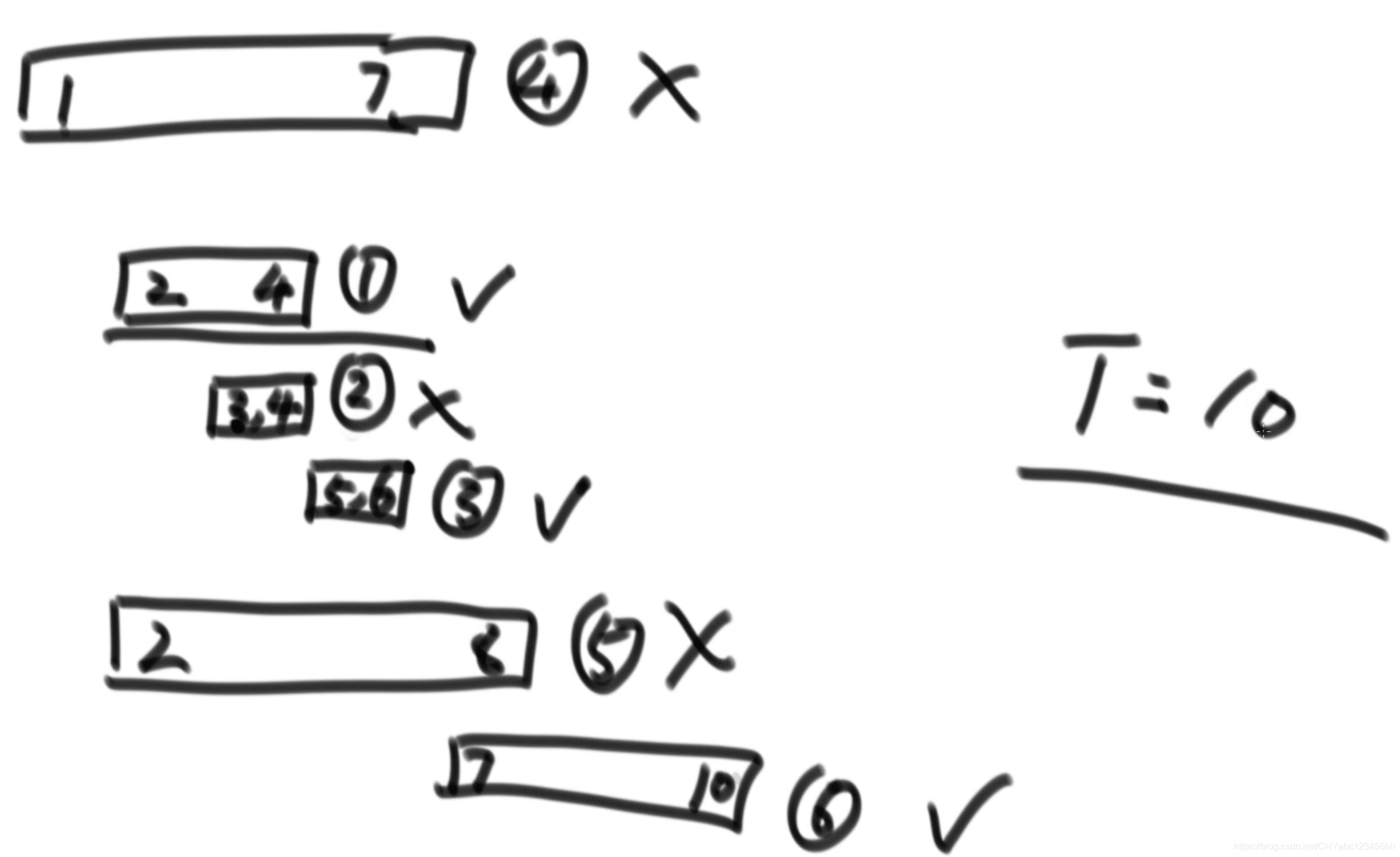
?代碼?
// package class07;import java.util.Arrays;
import java.util.Comparator;
import java.util.HashSet;public class Code04_BestArrange {public static class Program {public int start;public int end;public Program(int start, int end) {this.start = start;this.end = end;}}public static class ProgramComparator implements Comparator<Program> {@Overridepublic int compare(Program o1, Program o2) {return o1.end - o2.end;}}public static int bestArrange(Program[] programs, int timePoint) {Arrays.sort(programs, new ProgramComparator());int result = 0;// 從左往右依次遍歷所有的會議for (int i = 0; i < programs.length; i++) {if (timePoint <= programs[i].start) {result++;timePoint = programs[i].end;}}return result;}//使用暴力解法public static int bestArrangeForce(Program[] programs,int timePoint){HashSet<Program> set = new HasgSet<>(Arrays.asList(programs));}//會議的集合是set,當前時間是timePoint//返回集合中最多可以安排幾個項目public static int process(HashSet<Program>set ,int timepoint){HashSet<Program> candidates = new HashSet<>();for(Program program : set){if(program.start >= timepoint){candidates.add(program);}}//tmp只是為了使用迭代器HashSet<Program> tmp = new HashSet<>(candidates);int result = 0;//嘗試將每一個項目,作為第一個安排的項目for(Program program : tmp){candidates.remove(program);int next = process(candidates, program.end);result = Math.max(result,next+1);candidates.add(program);}return result;}public static void main(String[] args) {}}- 注意事項:對于HashSet集合中的元素,不可以一邊遍歷一邊刪除。需要使用一個tmp集合,將滿足條件條件的元素放到tmp中,然后遍歷tmp集合,刪除原有的集合中的元素
- 例子:將1到8元素放入到集合set中,需要刪除集合中小于5的元素,所以遍歷set集合,將小于5的元素收集到tmp集合中,然后遍歷tmp集合,刪除set集合中小于5的元素,最后遍歷打印set集合。
代碼
HashSet<Integer> set = new HashSet<>();set.add(1);set.add(2);set.add(3);set.add(4);set.add(5);set.add(6);set.add(7);set.add(8);HashSet<Integer> tmp = new HashSet<>();//刪除集合中比5小的數//不可以一邊遍歷一邊刪除元素for(Integer i : set){if(i < 5){tmp.add(i);}}for(Integer i : tmp){set.remove(i);}for(Integer i : set){System.out.println(i);}}題目要求
給定一個字符串類型的數組str,找到一種拼接方式,使得所有字符串拼接起來形成的字符串具有最小的字典序
- 字典序:兩個字符串在字典中誰先放在前面,誰的字典序就低
- 思路:兩個字符串,str1和str2,如果str1+str2的字典順序小于str2+str1,則將str1放到str2的前面,否則將str2放到str1的前面
- 排序具有傳遞性,不可以歧義,如果是閉環結構是不可以排序的
- “abc”*“xy”? ==> "abc" * K^2 + "xy" ;* K^2好比與將abc字符串向左邊移動2位,K暗指字符串是K進制的數字,數字2是指第二個需要拼接字符串的位數,然后加上字符串xy,整個的過程就像數字運算一樣。
- 使用m(str)= return(K^string長度),所以“abc”*“xy”? ==> "abc" * K^2 + "xy" ==> "abc" * m(xy) + "xy"
代碼
package class07;import java.util.Arrays;
import java.util.Comparator;public class Code02_LowestLexicography {public static class MyComparator implements Comparator<String> {@Overridepublic int compare(String a, String b) {return (a + b).compareTo(b + a);}}public static String lowestString(String[] strs) {if (strs == null || strs.length == 0) {return "";}Arrays.sort(strs, new MyComparator());String res = "";for (int i = 0; i < strs.length; i++) {res += strs[i];}return res;}public static void main(String[] args) {String[] strs1 = { "jibw", "ji", "jp", "bw", "jibw" };System.out.println(lowestString(strs1));String[] strs2 = { "ba", "b" };System.out.println(lowestString(strs2));}}圖片解析
- 根據給出的條件a . b 小于等于 b . a 和 b. c?小于等于 c?. b得出a . c 小于等于 c .?a,根據上面的式子,得出右邊的不等式,將第一個不等式的兩邊減去b 再乘以 c;第二個不等式左右兩邊 減去c 乘以a ,這樣兩個式子會產生一個重合的項,鏈接其余不等式,化簡之后就可以得到 m(c)* a + c 小于等于 m(a)*c + a
- ?
比較排序的過程:

分金條問題
思路
- 利用小根堆來做,每次選取其中最小的兩個數,合并成為一個數,放入到堆中,依次類推。當小根堆里面只有一個數字的時候,就是最終的答案。(哈夫曼編碼)
代碼
package class07;import java.util.Comparator;
import java.util.PriorityQueue;public class Code03_LessMoneySplitGold {public static int lessMoney(int[] arr) {PriorityQueue<Integer> pQ = new PriorityQueue<>();for (int i = 0; i < arr.length; i++) {pQ.add(arr[i]);}int sum = 0;int cur = 0;while (pQ.size() > 1) {cur = pQ.poll() + pQ.poll();sum += cur;pQ.add(cur);}return sum;}public static class MinheapComparator implements Comparator<Integer> {@Overridepublic int compare(Integer o1, Integer o2) {return o1 - o2; // < 0 o1 < o2 負數}}public static class MaxheapComparator implements Comparator<Integer> {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1; // < o2 < o1}}public static void main(String[] args) {// solutionint[] arr = { 6, 7, 8, 9 };System.out.println(lessMoney(arr));int[] arrForHeap = { 3, 5, 2, 7, 0, 1, 6, 4 };// min heapPriorityQueue<Integer> minQ1 = new PriorityQueue<>();for (int i = 0; i < arrForHeap.length; i++) {minQ1.add(arrForHeap[i]);}while (!minQ1.isEmpty()) {System.out.print(minQ1.poll() + " ");}System.out.println();// min heap use ComparatorPriorityQueue<Integer> minQ2 = new PriorityQueue<>(new MinheapComparator());for (int i = 0; i < arrForHeap.length; i++) {minQ2.add(arrForHeap[i]);}while (!minQ2.isEmpty()) {System.out.print(minQ2.poll() + " ");}System.out.println();// max heap use ComparatorPriorityQueue<Integer> maxQ = new PriorityQueue<>(new MaxheapComparator());for (int i = 0; i < arrForHeap.length; i++) {maxQ.add(arrForHeap[i]);}while (!maxQ.isEmpty()) {System.out.print(maxQ.poll() + " ");}}}求獲取的最大錢數

例子?
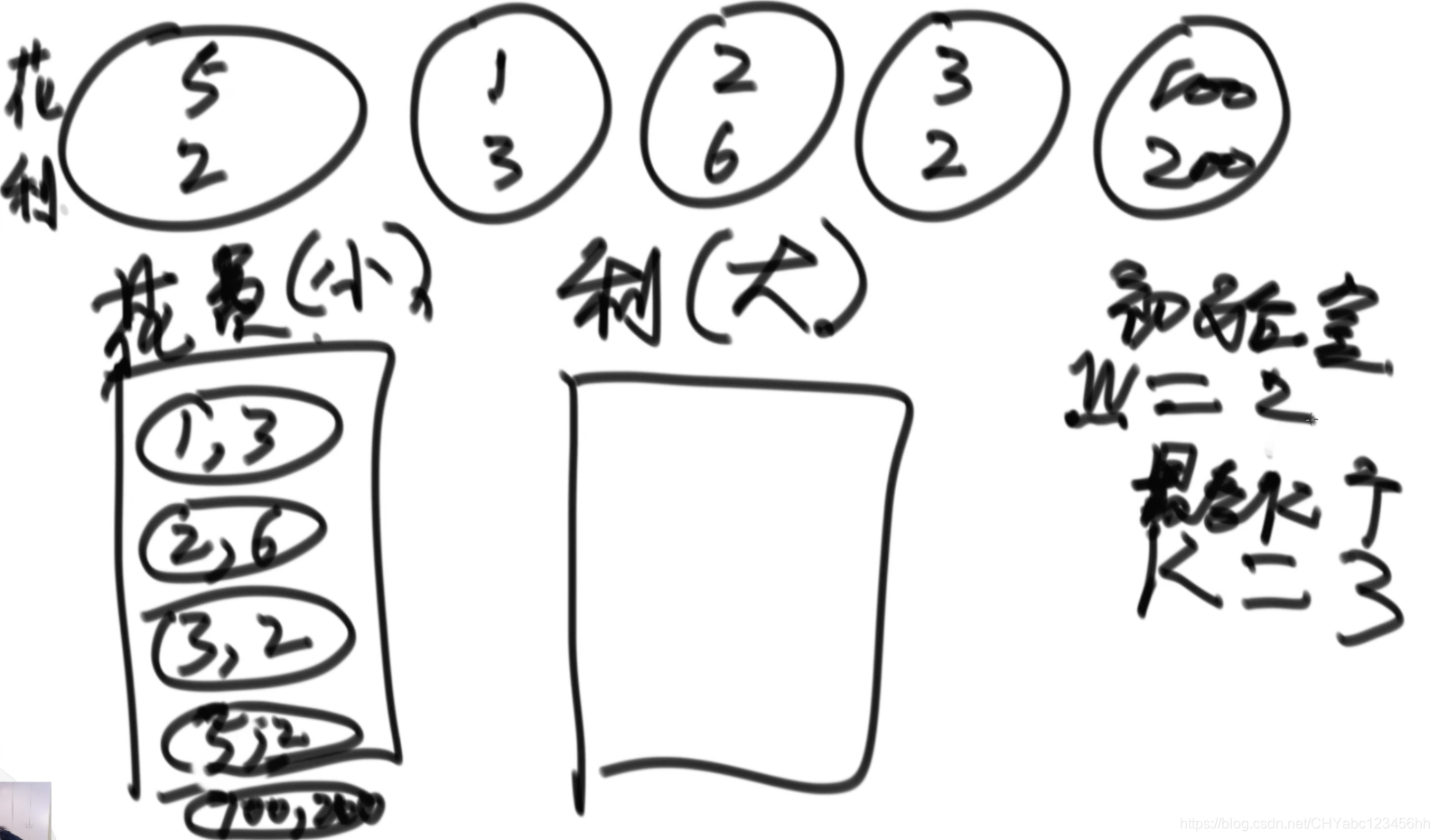
- 按照花費的錢建立小根堆,這個是被鎖定的狀態,根據初始的錢,比如w=2,解鎖(1,3)和(2,6)?,按照利潤的高低,壓入利潤大根堆中,(2,6)(1,3)加入棧中,然后將其從小根堆中刪除。然后做第一個項目(2,6),此時自己的錢數為8,那么將小于8的花費的項目解鎖,以此類推。
代碼
package class07;import java.util.Comparator;
import java.util.PriorityQueue;public class Code05_IPO {public static class Node {public int p;public int c;public Node(int p, int c) {this.p = p;this.c = c;}}public static class MinCostComparator implements Comparator<Node> {@Overridepublic int compare(Node o1, Node o2) {return o1.c - o2.c;}}public static class MaxProfitComparator implements Comparator<Node> {@Overridepublic int compare(Node o1, Node o2) {return o2.p - o1.p;}}public static int findMaximizedCapital(int k, int W, int[] Profits, int[] Capital) {PriorityQueue<Node> minCostQ = new PriorityQueue<>(new MinCostComparator());PriorityQueue<Node> maxProfitQ = new PriorityQueue<>(new MaxProfitComparator());// 所有項目扔到被鎖池中, 花費組織的小根堆for (int i = 0; i < Profits.length; i++) {minCostQ.add(new Node(Profits[i], Capital[i]));}for (int i = 0; i < k; i++) { // 進行K輪// 能力所及的項目,全解鎖while (!minCostQ.isEmpty() && minCostQ.peek().c <= W) {maxProfitQ.add(minCostQ.poll());}if (maxProfitQ.isEmpty()) {return W;}W += maxProfitQ.poll().p;}return W;}}
?
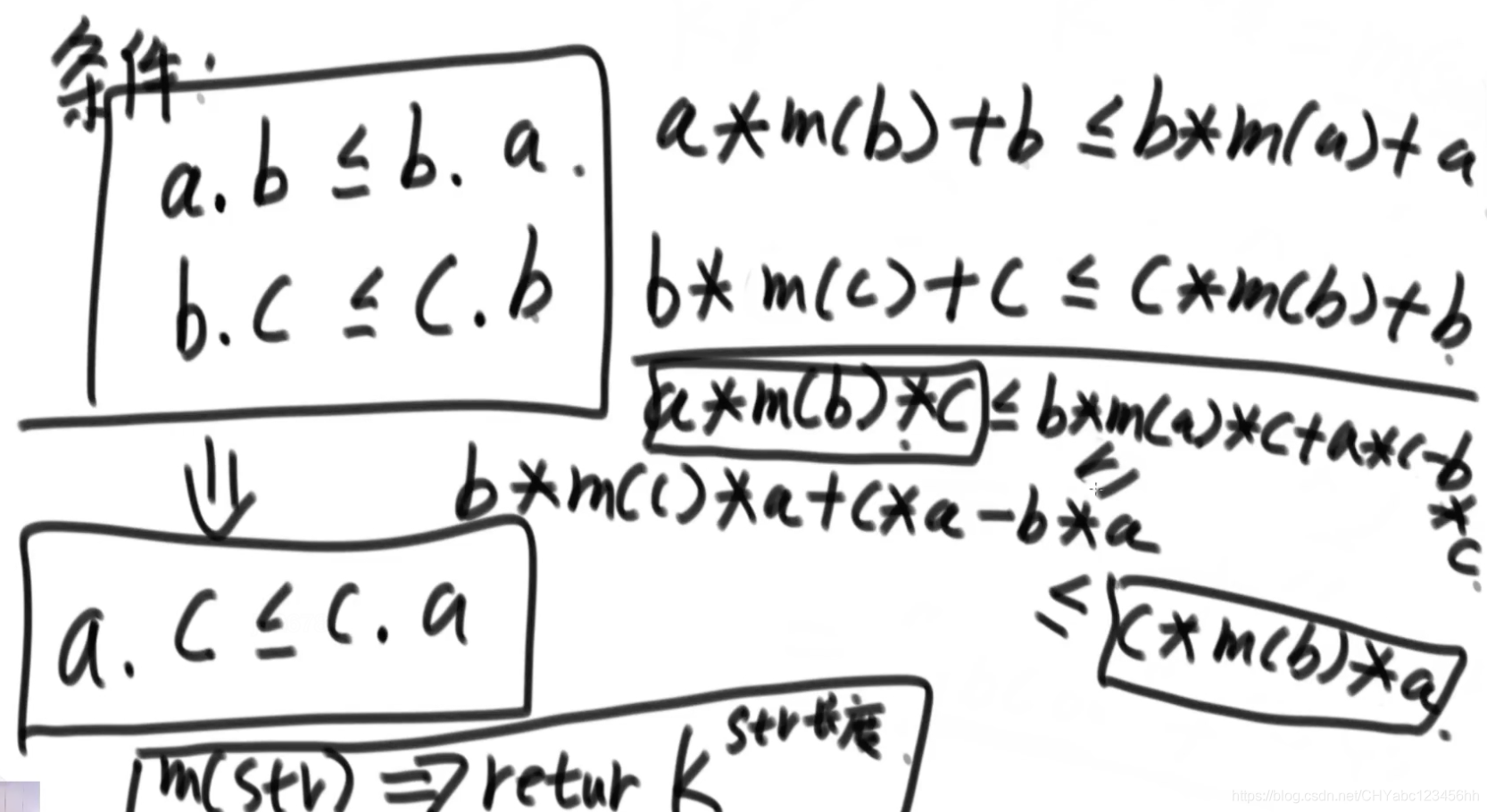













及其相關知識的講解)






