算法入門篇六 二叉樹

牛客網 算法入門篇 左程云老師 個人復習，如果侵全，設為私密

二叉樹遍歷（遞歸）

  • 先序遍歷（中，左，右）

  • 中序遍歷（左，中，右）

  • 后序遍歷（左，右，中）

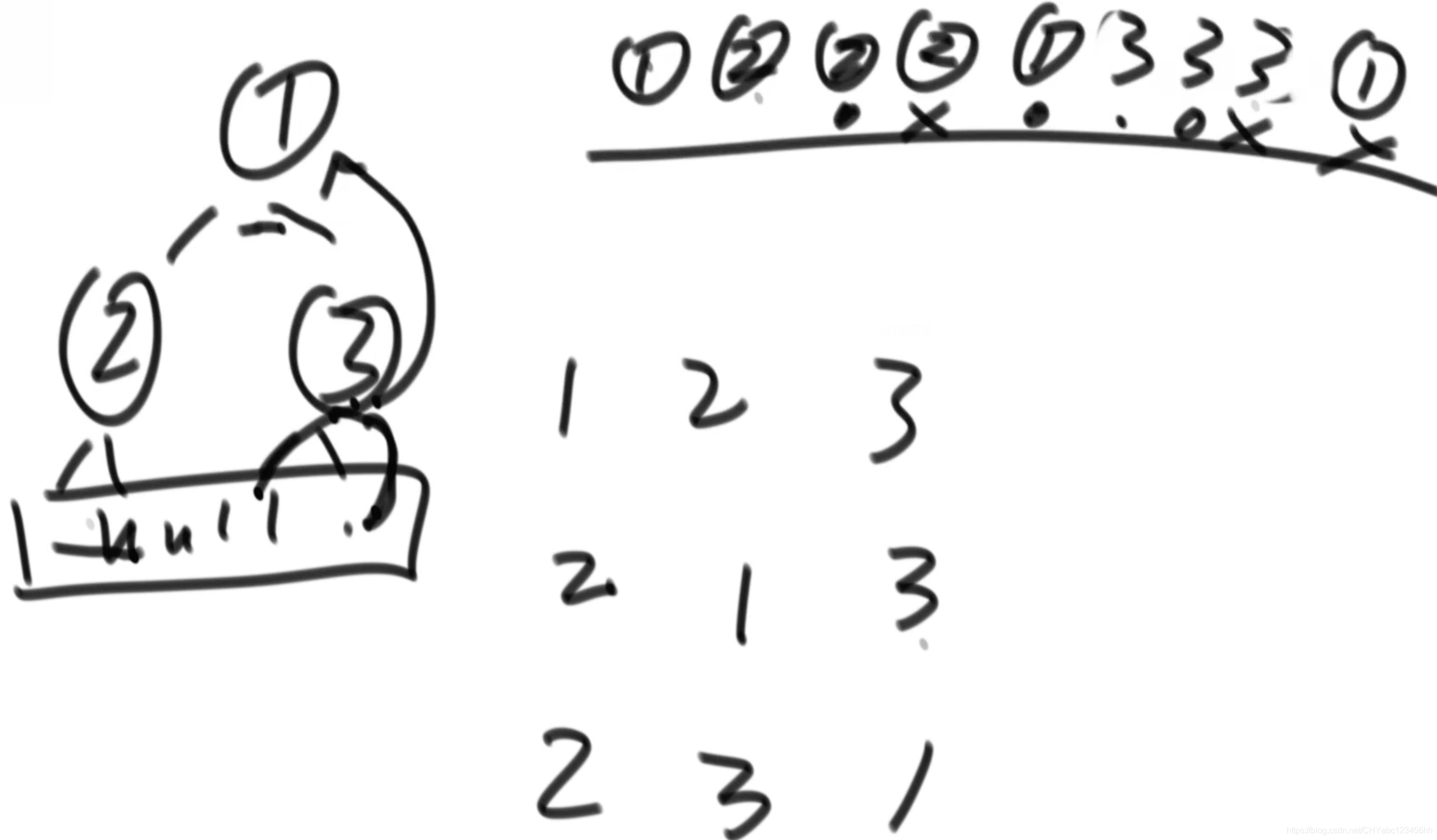
  • 如上圖所示結構，二叉樹的遍歷本質上都是遞歸序，1、2和3節點每個都會出現三次，比如從節點1出發，來到節點2，節點2的左邊為空，返回，打印2，右邊為空，返回打印2，再返回到節點1，節點3類似。所以最后輸出的序列為1，2，2，2，1，3，3，3，1。
  • 如果打印遞歸序出現的第1次的元素，就是先序遍歷
  • 如果打印遞歸序出現的第2次的元素，就是中序遍歷
  • 如果打印遞歸序出現的第3次的元素，就是后序遍歷

二叉樹遍歷（非遞歸）

先序遍歷

  • 二叉樹的結構如圖所示，準備一個棧用于接收數據
  • 原則只有兩點：1，棧中彈出節點叫做cur（當前節點），彈出就打印；2，先打印cur的右節點，仔打印左節點，沒有就無需操作。棧空就停止。
  • 1進棧，彈出1，打印1；將3和2壓入棧中，彈出2，打印2，將2的孩子節點4和5押入棧中；因為先押入右，再壓左，因此先將5押入，再押入4；彈出4，打印4；如上所述，先序遍歷為1，2，4，5，3，6，7

代碼

package class05;import java.util.Stack;public class Code01_PreInPosTraversal {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static void f(Node head) {// 1if (head == null) {return;}// 1f(head.left); //2//2f(head.right);// 3// 3}public static void preOrderRecur(Node head) {if (head == null) {return;}System.out.print(head.value + " ");preOrderRecur(head.left); preOrderRecur(head.right);}public static void inOrderRecur(Node head) {if (head == null) {return;}inOrderRecur(head.left);System.out.print(head.value + " ");inOrderRecur(head.right);}public static void posOrderRecur(Node head) {if (head == null) {return;}posOrderRecur(head.left);posOrderRecur(head.right);System.out.print(head.value + " ");}public static void preOrderUnRecur(Node head) {System.out.print("pre-order: ");if (head != null) {Stack<Node> stack = new Stack<Node>();stack.add(head);while (!stack.isEmpty()) {head = stack.pop();System.out.print(head.value + " ");if (head.right != null) {stack.push(head.right);}if (head.left != null) {stack.push(head.left);}}}System.out.println();}public static void inOrderUnRecur(Node head) {System.out.print("in-order: ");if (head != null) {Stack<Node> stack = new Stack<Node>();while (!stack.isEmpty() || head != null) {if (head != null) {stack.push(head);head = head.left;} else {head = stack.pop();System.out.print(head.value + " ");head = head.right;}}}System.out.println();}public static void posOrderUnRecur1(Node head) {System.out.print("pos-order: ");if (head != null) {Stack<Node> s1 = new Stack<Node>();Stack<Node> s2 = new Stack<Node>();s1.push(head);while (!s1.isEmpty()) {head = s1.pop();s2.push(head);if (head.left != null) {s1.push(head.left);}if (head.right != null) {s1.push(head.right);}}while (!s2.isEmpty()) {System.out.print(s2.pop().value + " ");}}System.out.println();}public static void posOrderUnRecur2(Node h) {System.out.print("pos-order: ");if (h != null) {Stack<Node> stack = new Stack<Node>();stack.push(h);Node c = null;while (!stack.isEmpty()) {c = stack.peek();if (c.left != null && h != c.left && h != c.right) {stack.push(c.left);} else if (c.right != null && h != c.right) {stack.push(c.right);} else {System.out.print(stack.pop().value + " ");h = c;}}}System.out.println();}public static void main(String[] args) {Node head = new Node(5);head.left = new Node(3);head.right = new Node(8);head.left.left = new Node(2);head.left.right = new Node(4);head.left.left.left = new Node(1);head.right.left = new Node(7);head.right.left.left = new Node(6);head.right.right = new Node(10);head.right.right.left = new Node(9);head.right.right.right = new Node(11);// recursiveSystem.out.println("==============recursive==============");System.out.print("pre-order: ");preOrderRecur(head);System.out.println();System.out.print("in-order: ");inOrderRecur(head);System.out.println();System.out.print("pos-order: ");posOrderRecur(head);System.out.println();// unrecursiveSystem.out.println("============unrecursive=============");preOrderUnRecur(head);inOrderUnRecur(head);posOrderUnRecur1(head);posOrderUnRecur2(head);}}

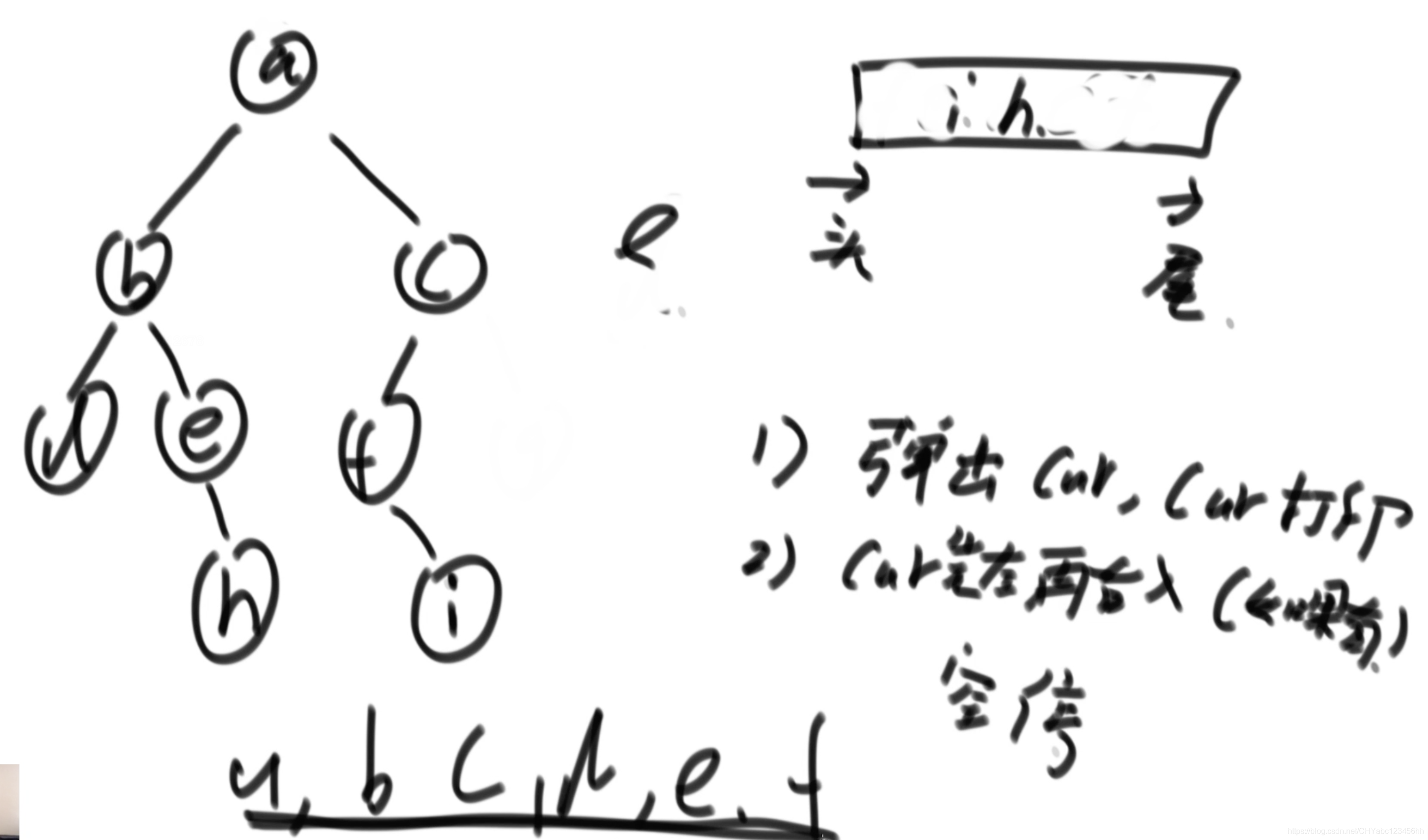
中序遍歷（非遞歸）

  • 原則只有兩點：1，棧中彈出節點叫做cur（當前節點），彈出就打印；2，先打印cur的左節點，仔打印右節點，沒有就無需操作。棧空就停止。
  • 不斷將右節點分成左和中節點

后序遍歷（非遞歸）

  • 原則只有兩點：1，棧中彈出節點叫做cur（當前節點），彈出不打印，放到一個新的棧中；2，最后將第二個棧中的元素打印，相當于是（左，右，中），即后序遍歷

直觀打印二叉樹

package class05;public class Code02_PrintBinaryTree {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static void printTree(Node head) {System.out.println("Binary Tree:");printInOrder(head, 0, "H", 17);System.out.println();}public static void printInOrder(Node head, int height, String to, int len) {if (head == null) {return;}printInOrder(head.right, height + 1, "v", len);String val = to + head.value + to;int lenM = val.length();int lenL = (len - lenM) / 2;int lenR = len - lenM - lenL;val = getSpace(lenL) + val + getSpace(lenR);System.out.println(getSpace(height * len) + val);printInOrder(head.left, height + 1, "^", len);}public static String getSpace(int num) {String space = " ";StringBuffer buf = new StringBuffer("");for (int i = 0; i < num; i++) {buf.append(space);}return buf.toString();}public static void main(String[] args) {Node head = new Node(1);head.left = new Node(-222222222);head.right = new Node(3);head.left.left = new Node(Integer.MIN_VALUE);head.right.left = new Node(55555555);head.right.right = new Node(66);head.left.left.right = new Node(777);printTree(head);head = new Node(1);head.left = new Node(2);head.right = new Node(3);head.left.left = new Node(4);head.right.left = new Node(5);head.right.right = new Node(6);head.left.left.right = new Node(7);printTree(head);head = new Node(1);head.left = new Node(1);head.right = new Node(1);head.left.left = new Node(1);head.right.left = new Node(1);head.right.right = new Node(1);head.left.left.right = new Node(1);printTree(head);}}

求二叉樹的最大寬度

使用隊列

  • 使用一個隊列，從頭部進入，從尾巴出來；
  • 原則：彈出當前節點cur，彈出并打印；當前節點的話存在左右節點的話，先放入左節點，再放入右節點。如果不存在孩子節點，等隊列為null的話，就停止輸出。但是，存在一個問題，我們不知道哪些節點是類屬于一層的，因此需要進行指定。需要引入哈希表來統計相關的層數、以及最大的跨度

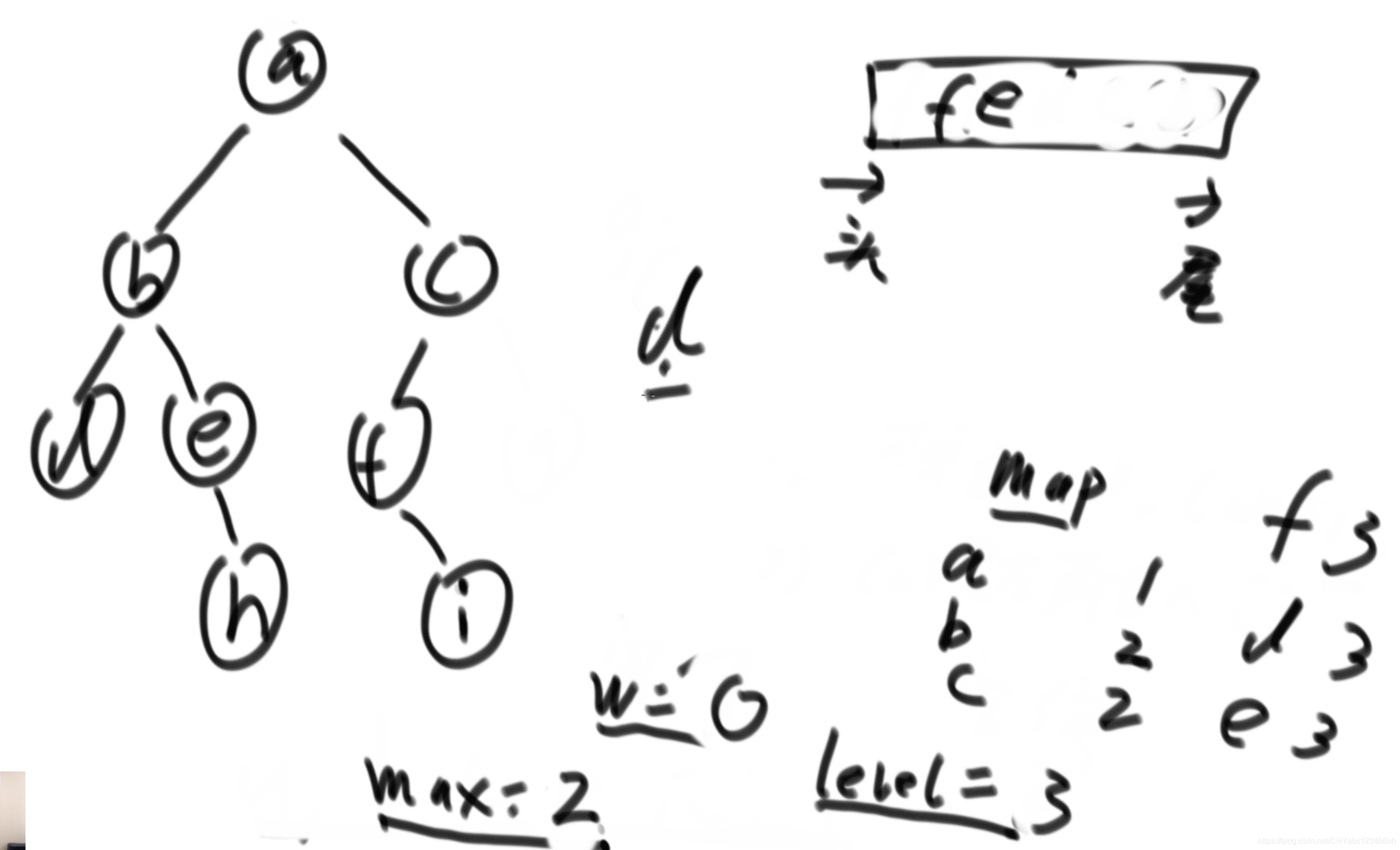
使用哈希表

  • 引入哈希表，設置三個變量，max為全局最大寬度，w為統計當前層級的寬度值，level記錄統計層級
  • 初始設置max=-1，w=0，level=1；當a輸入隊列，w變為1，level顯示當前層級為1，當a出隊列，將其孩子節點b和c放入隊列，當b出隊列，level查詢發現b是2層的，因此將w和max比較大小，將大的數值賦值給max，然后將w清除數據，重新統計第二層級的數的個數。以此類推。

代碼

package class05;import java.util.HashMap;
import java.util.LinkedList;
import java.util.Queue;public class Code03_TreeMaxWidth {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static int w(Node head) {if(head == null) {return 0;}Queue<Node> queue = new LinkedList<>();queue.add(head);HashMap<Node, Integer> levelMap = new HashMap<>();levelMap.put(head, 1);int curLevel = 1;int curLevelNodes = 0;int max = Integer.MIN_VALUE;while(!queue.isEmpty()) {Node cur = queue.poll();int curNodeLevel = levelMap.get(cur);if(curNodeLevel == curLevel) {curLevelNodes++;} else {max = Math.max(max, curLevelNodes);curLevel++;curLevelNodes = 1;}if(cur.left !=null) {levelMap.put(cur.left, curNodeLevel+1);queue.add(cur.left);}if(cur.right !=null) {levelMap.put(cur.right, curNodeLevel+1);queue.add(cur.right);}}return max;}public static int getMaxWidth(Node head) {if (head == null) {return 0;}int maxWidth = 0;int curWidth = 0;// 目前的層數int curLevel = 0;// node 所在的層數HashMap<Node, Integer> levelMap = new HashMap<>();levelMap.put(head, 1);LinkedList<Node> queue = new LinkedList<>();queue.add(head);Node node = null;Node left = null;Node right = null;while (!queue.isEmpty()) {node = queue.poll();left = node.left;right = node.right;if (left != null) {levelMap.put(left, levelMap.get(node) + 1);queue.add(left);}if (right != null) {levelMap.put(right, levelMap.get(node) + 1);queue.add(right);}if (levelMap.get(node) > curLevel) {curWidth = 1;curLevel = levelMap.get(node);} else {curWidth++;}maxWidth = Math.max(maxWidth, curWidth);//更新最后一層，因為最后一層沒有觸發邏輯}return maxWidth;}public static void main(String[] args) {// TODO Auto-generated method stub}}

?二叉樹的遞歸套路

如何判斷一棵樹是滿二叉樹

  • 性質 節點數 = 2^樹的高度 - 1
  • 思路 假設以x為頭節點，只有滿足性質才是一個滿二叉樹。在容許向左右兩個孩子要信息的前提下，應該要什么信息，才可以解決問題。
public class IsFull{public static class Node{public int value;public Node left;public Node right;public Node(int data){this.value = data;}}public static boolean isFull(Node head){Info info = processInfo(head);int size = info.size;int height = info.height;return size == (1<<height) - 1;}public static class Info{public int size;public int height;public Info(int s,int h){size = s;height = h;}}public static Info processInfo(Node x){if(x == 0){return new Info(0,0);}Info leftInfo = processInfo(x.left);Info rightInfo = processInfo(x.right);int size = leftInfo.size + rightInfo.size + 1;int height = Math.max(leftInfo.height,rightInfo.height) + 1;return new Info(size, height);}public static void main(String[] args) {}
}

方法歸納

  • 假設要求以x為頭的答案
  • 向左右兩個孩子要信息，去分析構成答案的主要元素
  • 確定向左右孩子要的信息，有可能左右要的信息不一樣
  • 組織收集到的信息

判斷以x為頭的二叉樹是否是平衡二叉樹

  • 判斷左右孩子的高度差是否相差小于等于1
  • 如果左右孩子不滿足平衡二叉樹，那么此平衡二叉樹不成立

代碼

import jdk.vm.ci.code.site.Infopoint;public class IsFull{public static class Node{public int value;public Node left;public Node right;public Node(int data){this.value = data;}}public static class Info{public boolean isBalanced;public int height;public Info(boolean is,int h){isBalanced = is;height = h;}}public static Info process(Node x){if(x == nll){return new Info(true,0);//return null;}Info leftInfo = process(x.left);Info rightInfo = process(x.right);int subTreeMaxHeight = 0;if(leftInfo != null){subTreeMaxHeight = leftInfo.height;}if(rightInfo!=null){subTreeMaxHeight = Math.max(subTreeMaxHeight,rightInfo.height);}int height = 1 + subTreeMaxHeight;boolean isBalanced = true;if(leftInfo!=null && !leftInfo.isBalanced){isBalanced=false;}if(rightInfo!= null && !rightInfo.isBalanced){isBalanced = false;}int leftH = leftInfo != null ? leftInfo.height : 0;int rightH = leftInfo != null ? rightInfo.height : 0; if(Math.abs(leftH - rightH)>1){isBalanced = false;}return new Infopoint(isBalanced, height);}public static void main(String[] args) {}
}

求樹中兩個節點的最大距離

情況分類

和頭節點x無關

  • 左樹上的最大距離
  • 右樹上的最大距離

和頭節點x相關

  • 左邊距離x最遠和x到右邊最遠距離（樹的高度）

代碼

import org.graalvm.compiler.nodes.calc.LeftShiftNode;
import org.graalvm.compiler.nodes.calc.RightShiftNode;import jdk.vm.ci.code.site.Infopoint;public class IsFull{public static int maxDistance(Node head){Info info = process(head);return info.maxDistance;}public static class Info{public int maxDistance;public int height;public Info(boolean is,int h){maxDistance = d;height = h;}}public static Info process(Node x){if(x == null){return new Info(0,0);}Info leftInfo = process(x.left);Info rightInfo = process(x.right);int height = Math.max(leftInfo.height,rightInfo.height) + 1;int maxDistance = Math.max(leftInfo.height + rightInfo.height + 1,Math.max(leftInfo.height,rightInfo.height));return new Info(maxDistance,height);}   public static void main(String[] args) {}
}

判斷一個樹是否是搜索二叉樹

套路

判定條件

  • 左樹是否是搜索二叉樹
  • 右樹是否是搜索二叉樹
  • 左邊最大的是否小于 x節點
  • 右邊最小的是否大于 x節點

代碼

package class05;import java.util.LinkedList;
import java.util.Stack;import class05.Code01_PreInPosTraversal.Node;public class Code04_IsBST {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static class ReturnData {public boolean isBST;public int min;public int max;public ReturnData(boolean is, int mi, int ma) {isBST = is;min = mi;max = ma;}}public static ReturnData process(Node x) {if(x == null) {return null;}ReturnData leftData = process(x.left);ReturnData rightData = process(x.right);int min = x.value;int max = x.value;if(leftData!=null) {min = Math.min(min, leftData.min);max = Math.max(max, leftData.max);}if(rightData!=null) {min = Math.min(min, rightData.min);max = Math.max(max, rightData.max);}
//      boolean isBST = true;
//      if(leftData!=null && (!leftData.isBST   ||  leftData.max >= x.value  )) {
//          isBST= false;
//      }
//      if(rightData!=null && ( !rightData.isBST || x.value >= rightData.min   )) {
//          isBST= false;
//      }boolean isBST = false;if((leftData != null ? (leftData.isBST  &&  leftData.max < x.value) : true)&&(rightData !=null ? (rightData.isBST  && rightData.min > x.value) : true)        ) {isBST = true;}return new ReturnData(isBST, min, max);}public static boolean isF(Node head) {if(head == null) {return true;}Info data = f(head);return data.nodes == (1 << data.height - 1);}public static class Info{public int height;public int nodes;public Info(int h, int n) {height = h;nodes = n;}}public static Info f(Node x) {if(x == null) {return new Info(0,0);}Info leftData = f(x.left);Info rightData = f(x.right);int height  = Math.max(leftData.height,rightData.height)+1;int nodes = leftData.nodes + rightData.nodes + 1;return new Info(height, nodes);}public static boolean inOrderUnRecur(Node head) {if (head == null) {return true;}int pre = Integer.MIN_VALUE;Stack<Node> stack = new Stack<Node>();while (!stack.isEmpty() || head != null) {if (head != null) {stack.push(head);head = head.left;} else {head = stack.pop();if (head.value <= pre) {return false;}pre = head.value;head = head.right;}}return true;}public static boolean isBST(Node head) {if (head == null) {return true;}LinkedList<Node> inOrderList = new LinkedList<>();process(head, inOrderList);int pre = Integer.MIN_VALUE;for (Node cur : inOrderList) {if (pre >= cur.value) {return false;}pre = cur.value;}return true;}public static void process(Node node, LinkedList<Node> inOrderList) {if (node == null) {return;}process(node.left, inOrderList);inOrderList.add(node);process(node.right, inOrderList);}}

也可以中序遍歷

  • 只要遞增，就是搜索二叉樹

  • 基于非遞歸中序遍歷改進，由先前的打印，變為和前一個節點比較

代碼

public static boolean inOrderUnRecur(Node head){if(head == null){return true;}int pre = Integer.MIN_VALUE;Stack<Node> stack = new Stack<Node>();while(!stack.isEmpty() || head != null){if(head != null){stack.push(head);head = head.left;}else{head = stack.pop();if(head.value <= pre){return false;}pre = head.value;head = head.right;}}return true;}

不可以使用套路來做

判斷一棵樹是否是完全二叉樹

  • 如果使用條件，左子樹是否是完全二叉樹，右子樹是否是完全二叉樹來判定根節點是否是完全二叉樹

  • 即使左子樹和右子樹都是完全二叉樹，但是左子樹比右子樹少整整一層的情形下，判定失敗

思路

  • 寬度優先遍歷，任何一個節點不能有右節點，沒有左節點。
  • 當第一次發現某節點左右不雙全，后續節點都是右節點
package class05;import java.util.LinkedList;public class Code05_IsCBT {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static boolean isCBT(Node head) {if (head == null) {return true;}LinkedList<Node> queue = new LinkedList<>();// 是否遇到過左右兩個孩子不雙全的節點boolean leaf = false;Node l = null;Node r = null;queue.add(head);while (!queue.isEmpty()) {head = queue.poll();l = head.left;r = head.right;if (// 如果遇到了不雙全的節點之后，又發現當前節點不是葉節點(leaf && !(l == null && r == null)) || (l == null && r != null)) {return false;}if (l != null) {queue.add(l);}if (r != null) {queue.add(r);}if (l == null || r == null) {leaf = true;}}return true;}}

求n1和n2的最低公共主先

劃分情況（x為頭節點）

  • x無n1和n2
  • x只有n1
  • x只有n2
  • x有n1和n2：左n1n2；右n1n2；左n1右n2；左n2右n1

代碼

package class05;import java.util.HashMap;
import java.util.HashSet;public class Code07_LowestCommonAncestor {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static Node lowestAncestor(Node head, Node o1, Node o2) {if (head == null || head == o1 || head == o2) { // base casereturn head;}Node left = lowestAncestor(head.left, o1, o2);Node right = lowestAncestor(head.right, o1, o2);if (left != null && right != null) {return head;}// 左右兩棵樹，并不都有返回值return left != null ? left : right;}public static class Record1 {private HashMap<Node, Node> map;public Record1(Node head) {map = new HashMap<Node, Node>();if (head != null) {map.put(head, null);}setMap(head);}private void setMap(Node head) {if (head == null) {return;}if (head.left != null) {map.put(head.left, head);}if (head.right != null) {map.put(head.right, head);}setMap(head.left);setMap(head.right);}public Node query(Node o1, Node o2) {HashSet<Node> path = new HashSet<Node>();while (map.containsKey(o1)) {path.add(o1);o1 = map.get(o1);}while (!path.contains(o2)) {o2 = map.get(o2);}return o2;}}public static class Record2 {private HashMap<Node, HashMap<Node, Node>> map;public Record2(Node head) {map = new HashMap<Node, HashMap<Node, Node>>();initMap(head);setMap(head);}private void initMap(Node head) {if (head == null) {return;}map.put(head, new HashMap<Node, Node>());initMap(head.left);initMap(head.right);}private void setMap(Node head) {if (head == null) {return;}headRecord(head.left, head);headRecord(head.right, head);subRecord(head);setMap(head.left);setMap(head.right);}private void headRecord(Node n, Node h) {if (n == null) {return;}map.get(n).put(h, h);headRecord(n.left, h);headRecord(n.right, h);}private void subRecord(Node head) {if (head == null) {return;}preLeft(head.left, head.right, head);subRecord(head.left);subRecord(head.right);}private void preLeft(Node l, Node r, Node h) {if (l == null) {return;}preRight(l, r, h);preLeft(l.left, r, h);preLeft(l.right, r, h);}private void preRight(Node l, Node r, Node h) {if (r == null) {return;}map.get(l).put(r, h);preRight(l, r.left, h);preRight(l, r.right, h);}public Node query(Node o1, Node o2) {if (o1 == o2) {return o1;}if (map.containsKey(o1)) {return map.get(o1).get(o2);}if (map.containsKey(o2)) {return map.get(o2).get(o1);}return null;}}// for test -- print treepublic static void printTree(Node head) {System.out.println("Binary Tree:");printInOrder(head, 0, "H", 17);System.out.println();}public static void printInOrder(Node head, int height, String to, int len) {if (head == null) {return;}printInOrder(head.right, height + 1, "v", len);String val = to + head.value + to;int lenM = val.length();int lenL = (len - lenM) / 2;int lenR = len - lenM - lenL;val = getSpace(lenL) + val + getSpace(lenR);System.out.println(getSpace(height * len) + val);printInOrder(head.left, height + 1, "^", len);}public static String getSpace(int num) {String space = " ";StringBuffer buf = new StringBuffer("");for (int i = 0; i < num; i++) {buf.append(space);}return buf.toString();}public static void main(String[] args) {Node head = new Node(1);head.left = new Node(2);head.right = new Node(3);head.left.left = new Node(4);head.left.right = new Node(5);head.right.left = new Node(6);head.right.right = new Node(7);head.right.right.left = new Node(8);printTree(head);System.out.println("===============");Node o1 = head.left.right;Node o2 = head.right.left;System.out.println("o1 : " + o1.value);System.out.println("o2 : " + o2.value);System.out.println("ancestor : " + lowestAncestor(head, o1, o2).value);System.out.println("===============");}}

?

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/447213.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/447213.shtml
英文地址，請注明出處：http://en.pswp.cn/news/447213.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

VLC詳細的使用說明以及配置說明綜合示范實例精通VLC開發

VLC詳細的使用說明以及配置說明綜合示范實例精通VLC開發

vlc的全名是Video LanClient&#xff0c;是一個開源的、跨平臺的視頻播放器。VLC支持大量的音視頻傳輸、封裝和編碼格式&#xff0c;完整的功能特性列表可以在這里獲得http://www.videolan.org/vlc/features.html&#xff0c;下面給出一個簡要的不完整的列表&#xff1a;操作系…
閱讀更多...
算法入門篇七 前綴樹

算法入門篇七 前綴樹

牛客網 左程云老師的算法入門課 找二叉樹的節點的后繼節點 原則 如果節點有右子樹&#xff0c;那么后繼節點就是右子樹的最左邊的第一個節點如果節點沒有右子樹&#xff0c;如果節點是父節點的右孩子&#xff0c;就繼續往上找&#xff0c;直到找到一個父節點是沿途節點的父節…
閱讀更多...
VLC視頻播放器原理詳細分析含TS流格式分析

VLC視頻播放器原理詳細分析含TS流格式分析

vlc是一個功能強大的玩意&#xff0c;能做很多有意思的事情。最簡單的&#xff0c;從界面打開一個文件播放&#xff0c;也可以在命令行下使用&#xff0c;如C:\Program Files\VideoLAN\VLC>vlc.exe test.ts獲取內置的幫助&#xff0c;會寫到vlc-help.txtC:\Program Files\Vi…
閱讀更多...
算法入門篇八 貪心算法

算法入門篇八 貪心算法

牛客網 左程云老師的算法入門課 貪心算法 貪心算法的解題步驟 例子 題目要求 解題策略 按照結束時間早的會議先安排&#xff0c;比如先安排【2&#xff0c;4】&#xff0c;當4結束了&#xff0c;所有開始時間小于4的全部淘汰&#xff0c;【1&#xff0c;7】、【3&#xff…
閱讀更多...
算法入門篇九 暴力遞歸

算法入門篇九 暴力遞歸

牛客網 左程云老師的算法入門課 暴力遞歸 原則 漢諾塔問題 問題 打印n層漢諾塔從左邊移動到最右邊的過程 思想 一共六個過程&#xff0c;左到右、左到中&#xff0c;中到左&#xff0c;中到右&#xff0c;右到左&#xff0c;右到中&#xff0c;互相嵌套使用 左到右 將1…
閱讀更多...
rtsp和sdp

rtsp和sdp

RTSP 是由Realnetwork 和Netscape共同提出的如何有效地在IP網絡上傳輸流媒體數據的應用層協議 。 實時流協議&#xff08;RTSP&#xff09;建立并控制一個或幾個時間同步的連續流媒體&#xff0c;如音頻和視頻。盡管連續媒體流與控制流交叉是可能的&#xff0c;RTSP本身并不發…
閱讀更多...
使用javascript實現對于chineseocr的API調用

使用javascript實現對于chineseocr的API調用

ChineseOCR在線API 網頁地址 界面 提供多種接口調用方式&#xff0c;比如在線調用、Javascript api調用、curl api調用和python api調用四種方式&#xff0c;本次使用javascript api調用的方式進行OCR識別在線Javascript工具 在線工具網頁鏈接在線Base64 轉化工具 在線工具…
閱讀更多...
移動流媒體業務的技術與標準

移動流媒體業務的技術與標準

1 引言 　　流媒體業務是從Internet上發展起來的一種多媒體應用&#xff0c;指使用流&#xff08;Streaming&#xff09;方式在網絡上傳輸的多媒體文件&#xff0c;包括音頻、視頻和動畫等。 　　流媒體傳輸技術的主要特點是以流&#xff08;streaming&#xff09;的形式進行多…
閱讀更多...
使用python實現對于chineseocr的API調用

使用python實現對于chineseocr的API調用

ChineseOCR在線API 網頁鏈接 界面 提供多種接口調用方式&#xff0c;比如在線調用、Javascript api調用、curl api調用和python api調用四種方式&#xff0c;本次使用javascript api調用的方式進行OCR識別在線Base64 轉化工具 Base64在線小工具代碼修改 新增一個變量fill_w…
閱讀更多...
UDP穿透NAT

UDP穿透NAT

NAT(Network AddressTranslators)&#xff0c;網絡地址轉換&#xff1a; 網絡地址轉換是在IP地址日益缺乏的情況下產生的&#xff0c;它的主要目的就是為了能夠地址重用。NAT分為兩大類&#xff0c;基本的NAT和NAPT(Network Address/Port Translator)。 最開始NAT是運行在路由器…
閱讀更多...
算法入門篇十 圖

算法入門篇十 圖

圖的存儲方式 臨接表臨接矩陣 表達 點集/邊集有向圖/無向圖 Graph&#xff08;大結構就是圖&#xff09;&#xff08;包含點集合和邊集合&#xff09; import java.util.HashMap; import java.util.HashSet;public class Graph {public HashMap<Integer, Node> nodes;…
閱讀更多...
SDP協議 學習筆記

SDP協議 學習筆記

SDP:Session Description ProtocolSDP格式:Session descriptionv (protocolversion)o (owner/creatorand session identifier)s (sessionname)i* (sessioninformation)u* (URI ofdescription)e* (emailaddress)p* (phonenumber)c*(connection information - not required if in…
閱讀更多...
以太坊私有鏈 使用dev模式

以太坊私有鏈 使用dev模式

dev 使用dev模式&#xff0c;創建一個管理員賬號&#xff0c;控制挖礦&#xff0c;將證明機制改為POA啟動dev模式&#xff0c;需要重新創建一個文件夾&#xff0c;重新搭建私有鏈條 命令 mkdir myDevChain cd myDevChain geth --datadir . --dev console 2>output.log 實…
閱讀更多...
超文本傳輸協議

超文本傳輸協議

超文本傳輸協議 超文本傳輸協議超文件傳輸協定(HTTP&#xff0c;HyperTextTransfer Protocol)是因特網上應用最為廣泛的一種網絡傳輸協定。所有的WWW文件都必須遵守這個標準。設計HTTP最初的目的是為了提供一種發布和接收HTML頁面的方法。 目錄 介紹請求信息請求方法安全方法超…
閱讀更多...
以太坊區塊鏈 JSON-RPC

以太坊區塊鏈 JSON-RPC

RPC定義 以太坊客戶端提供了API和一組遠程調用的&#xff08;RPC&#xff09;命令&#xff0c;這些命令被編碼成json的格式&#xff0c;被叫做JSON-RPC-API。本質上&#xff0c;JSON-RPC API就是一個接口&#xff0c;允許我們編寫的程序使用以太坊客戶端作為網關&#xff0c;訪…
閱讀更多...
利用MFC調用libvlc.dll作一個簡單的播放器

利用MFC調用libvlc.dll作一個簡單的播放器

簡單介紹MFC調用libvlc.dll作一個簡單的播放器&#xff0c;拋磚引玉&#xff0c;各位VC達人繼續深入研究&#xff0c;Jeremiah對VC確實不太感興趣&#xff0c;所以就不做太深入的研究了。2009.10.29修改&#xff1a;加入clip_children屬性設置。參開第1步。環境&#xff1a; …
閱讀更多...
對于以太坊虛擬機 （EVM）及其相關知識的講解

對于以太坊虛擬機 （EVM）及其相關知識的講解

以太坊虛擬機&#xff08;EVM&#xff09; EVM是智能合約的運行環境作為區塊驗證協議的一部分&#xff0c;參與網絡的每個節點都會運行EVM&#xff0c;審查節點會檢查驗證正在驗證的區塊中列出的交易&#xff0c;并運行EVM中交易觸發的代碼EVM是沙盒封裝的&#xff0c;并且是完…
閱讀更多...
對于以太坊的Solidity語言介紹

對于以太坊的Solidity語言介紹

Solidity是什么 Solidity是一門面向合約的、為實現智能合約而創建的高級編程語言&#xff0c;主要目的是為了在以太坊虛擬機&#xff08;EVM&#xff09;上運行Solidity是靜態語言&#xff0c;支持繼承、庫和復雜的用戶定義等特性內含的類型除了常見的編程語言中的標準類型&am…
閱讀更多...
live555 接收rtsp視頻流流程分析

live555 接收rtsp視頻流流程分析

live555 接收rtsp視頻流流程分析 RTSP交互流程 C表示RTSP客戶端&#xff0c;S表示RTSP服務端 ① C->S: OPTIONrequest //詢問S有哪些方法可用 S->C: OPTION response //S回應信息中包括提供的所有可用方法 ② C->S: DESCRIBErequest //要求得到S…
閱讀更多...
使用Remix編寫Solidity語言的小例子

使用Remix編寫Solidity語言的小例子

設置數值/取數值/加法運算 講解 uint默認使用256位數的整型view表示這個函數僅僅對于數據僅僅是讀取&#xff0c;沒有修改操作returns(uint )&#xff0c;如果單純指定uint&#xff0c;返回的是函數體內的return值&#xff0c;如果包含uint sum,uint SAD_a&#xff0c;那么返…
閱讀更多...
最新文章

Copyright @ 2022~2023