操作流程
- 選擇本地的需要轉換的文件
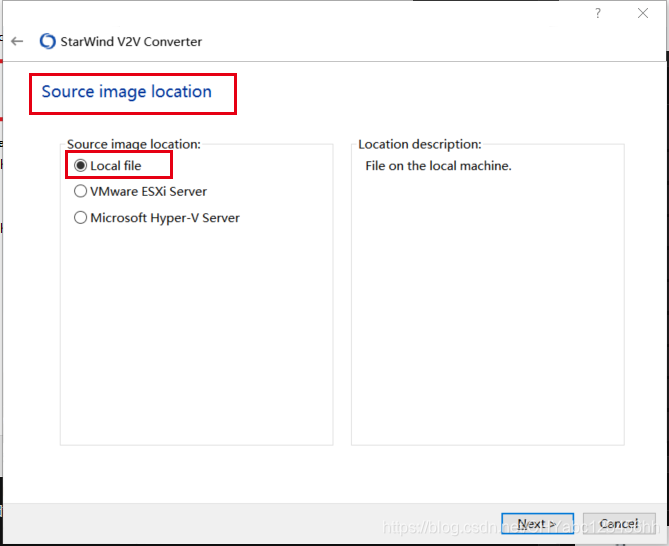
- 找到源文件的路徑，img格式
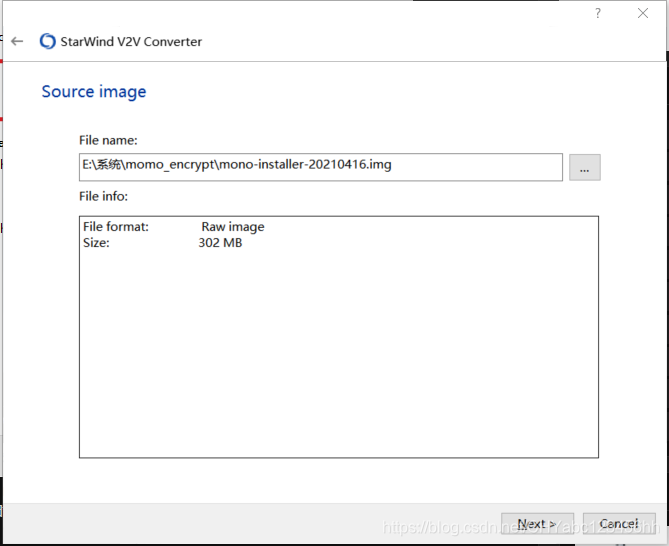
- 選擇轉化后的格式 第一個
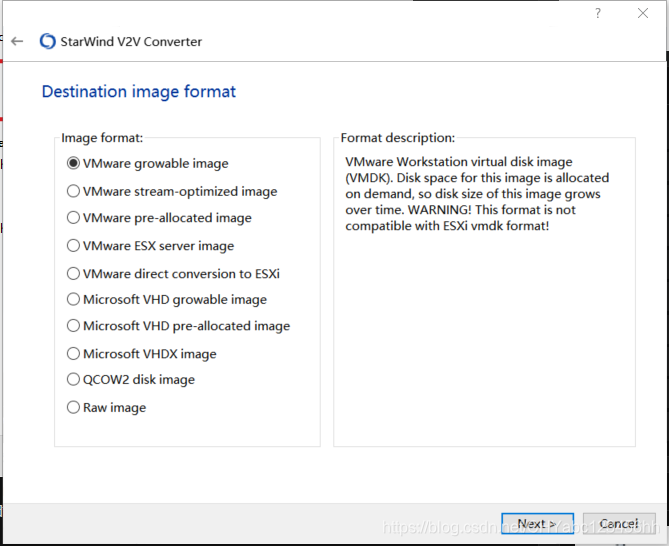
- 選擇 第二個 速度快一些
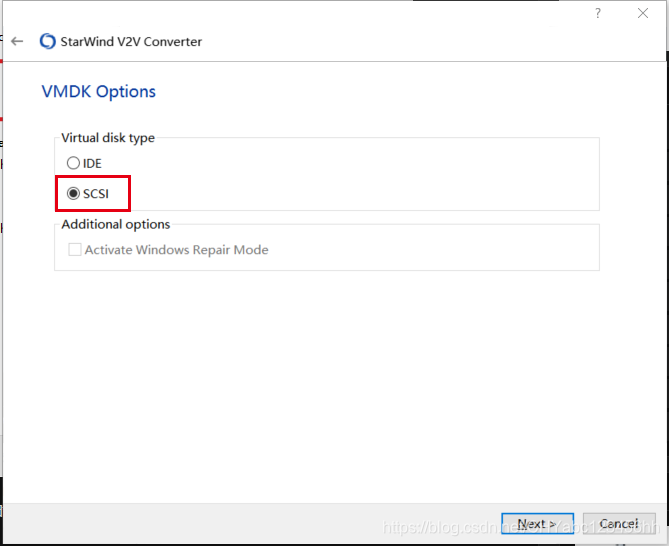
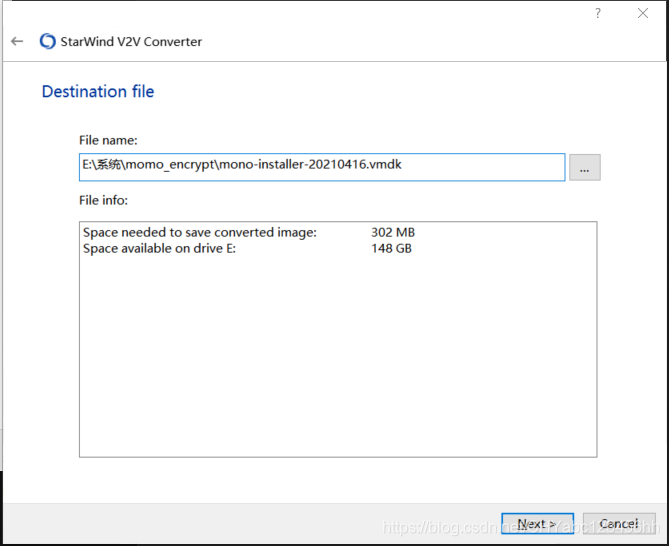
- 選擇將轉化后的文件的存儲路徑
軟件的下載鏈接
- 鏈接:?https://pan.baidu.com/s/1Fe6yI42Zz9d_Q7aUhGe1FQ?提取碼: 5vmv
StarWind V2V Image Converter：虛擬機鏡像轉換工具，可將 IMG 文件轉換為 VMware VMDK 文件
本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。 如若轉載，請注明出處：http://www.pswp.cn/news/446518.shtml 繁體地址，請注明出處：http://hk.pswp.cn/news/446518.shtml 英文地址，請注明出處：http://en.pswp.cn/news/446518.shtml
如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！相關文章
數學建模 線性規劃模型基本原理
線性規劃問題 例1.1 可行解&可行域
matlab標準形式及軟件求解
標準形式: C稱為價值向量 如果是求max,加一個負號-c^T 如果是求Ax>b,加一個負號-Ax<b
使用matlab求線性規劃例題
求解的是最大值:加上負號 y是求解的最優解
zeros()使用: zeros(n)：生…
裝有系統，將其中系統安裝到另外一塊磁盤的具體操作)
接上文 ，解決 虛擬機VM，U盤(磁盤)裝有系統，將其中系統安裝到另外一塊磁盤的具體操作
問題原因：接上文，將生成的vsdk格式的磁盤導入VM創建鏡像，相關于U盤裝載系統鏡像，將U盤其中的鏡像導入到磁盤里邊，U盤是引導，會將系統最終裝載到磁盤出錯原因是因為 沒有新建第二塊磁盤
解決 新增一塊磁盤如…
數學建模 層次分析法
簡介
針對多目標,多準則或無結構特性的復雜決策問題
步驟 解決評價類問題
評價類問題: 資料查找: 1)查找相關文獻 2)如果沒有找到相關文獻 3)搜索
通過上述步驟后得到的結果 構建層次結構模型 舉例:
成對比較矩陣 標度表: 奇數:越大越重要 偶數:上述兩相鄰判斷的中值…
ubuntu配置靜態IP地址
sysconf_client update -t network -j {"netdev":"eth0","ip":"a.b.c.d","mask":"255.255.255.0"}
接上文 VM安裝的ubuntu系統，配置雙網卡
點擊編輯 進入虛擬網絡編輯器 點擊更改設置 補充：如何判定橋接至哪張網卡？進入win，winr 輸入cmd；輸入 systeminfo選中系統，點擊右鍵，選中設置 重啟系統使用 ifconfig查看，發現有eth0和eth1…
)
數學建模 趣味數模問題(數模入門)
狼羊人菜渡河問題 解答
試探法 因為有4個變量,所以一共有222*216種狀態 找出其中不安全的狀態:無人看守的狀態下:狼羊一起,羊菜一起 人 狼 羊 菜(0是在對面,1是在這邊) 狼羊一起:(0,1,1,0) (0,1,1,1) (1,0,0,0) (1,0,0,1) 羊菜一起:(0,0,1,1) (1,1,0,0) 其余的10個都是安全狀態…
數學建模 整數規劃的基本原理和標準形式
整數規劃模型
變量限制為整數 一般解決運輸問題和整數問題 分類: 研究的是純整數規劃問題
整數規劃特點
實數的解不能直接四舍五入為整數,因為此時可能不滿足約束條件
舉例-合理下料問題 模型: 題目: 這是在使用材料 1)使用零件A1-Am毛胚,就是使用零件 2)下料方式B1-Bn就…
程序員 面試筆記 C++ 程序設計的基礎 第10章
10.1.1 程序的編譯和執行 以#開頭的代碼都屬于預處理器處理的步驟#include 將頭文件的內容包含進入當前源文件中#define 展開宏定義#ifdef 處理條件編譯指令(#ifdef、ifndef、#if、#else、#elif、#endif)#other 處理其他宏指令(#error、#warning、#line、#pragma)
預…
數學建模 分支限界算法求解整數規劃原理以及編程實現
引入
線性規劃問題(松弛問題) 圖解法: 使用圖解法求出最優解,再使用四舍五入求出的整數解不滿足條件 完全枚舉法(窮舉法):找出集合內所有滿足條件的整數點,再帶入不等式中,看是否有最優解
分支限界法
說明: 松弛問題:線性規劃問題 ILP:整數規劃,在線性規劃的基礎上對決策…
java Map統計字符串中元素的數量
public int firstUniqChar(String s) {Map<Character, Integer> map new HashMap();char[] chars s.toCharArray();//先統計每個字符的數量for (char ch : chars) {map.put(ch, map.getOrDefault(ch, 0) 1);}//然后在遍歷字符串s中的字符，如果出現次數是1就…
數學建模 割平面算法求解整數規劃基本原理與編程實現
基本思想
松弛問題:線性規劃 割掉一塊全部都是小數的區域(這一部分取不到整數)
案例
1)橫坐標x1,縱坐標x2 2)藍色小三角形的區域:x2:(1,7/4) x1:(0,3/4) 這塊區域,x1與x2完全取不到整數,所以直接切去
所以,此時取值范圍變化了: x2<1把此約束條件帶入,得到x11,x21,z2
3…
Linux dd命令 復制（拷貝）文件，并對原文件進行轉換
dd，是 device driver 的縮寫，它可以稱得上是“Linux 世界中的搬運工”，它用來讀取設備、文件中的內容，并原封不動地復制到指定位置。其實現在的主流硬盤已經是 SATA 接口的了，下面我要備份的硬盤是 dev/sda，…
數學建模 匈牙利算法求解整數規劃基本原理與編程實現
投資問題(0-1規劃)
匈牙利算法求解0-1規劃問題 解答: 項目之間是互斥關系,所以使用x1x2x31; 項目5是以項目1為先驗條件,所以x5<x1,意味著x11時,x51或0 ,但x10時,x50
案例- 互斥約束問題
1)當兩個約束條件是互斥時,新建立一個約束條件y(0-1) 2)如果M取無窮大的數,此時就…
Ubuntu通過可視化界面配置 查找IP地址不存在的解決辦法
命令行用ifconfig eno0 up，啟用網卡，沒有問題，硬件ok，但是配置里面還是找不到。之前修改了 /etc/network/interfaces，去掉配置。由于圖形界面使用的是 network-manager，所以需要修改重啟sudo service netwo…
數學建模 非線性規劃原理的應用與編程實現
非線性規劃模型NP
包含非線性函數:不是直線而是曲線、曲面、或不確定的屬性,叫非線性。 如:x^2 線性函數:一次函數,axb
列1-投資決策問題 解答: 設置決策變量: 1)投資某個項目達到收益最高,使用比值法(更直觀) 收益/投資花費 取值范圍 1)*非線性規劃中常用 限制xi0或1(在編…
數學建模1 賽前準備 賽題選擇 查找文獻
了解國賽
生成了MD5碼之后就不能再碰文件，打開都不行
軟件安裝 其他 ABC賽題特點
一般選擇B,C題
賽題選擇
1.排除背景都看不懂的題
定題
1.少數服從多數 2.選擇資料多的題
搜索技巧
1.雙引號–“CT參數標定”（內容或標題一致） 2…
劍指offer 第一章 面試的流程
面試的流程
面試的三種形式
電話面試：形象化語言講解細節；如果沒有聽清楚和聽懂問題，不要不懂裝懂，答非所問共享桌面，遠程面試：編程習慣和調試能力。1，思考清楚再開始編碼，先想思路…