整數規劃模型
變量限制為整數
一般解決運輸問題和整數問題
分類:
研究的是純整數規劃問題
整數規劃特點
實數的解不能直接四舍五入為整數,因為此時可能不滿足約束條件
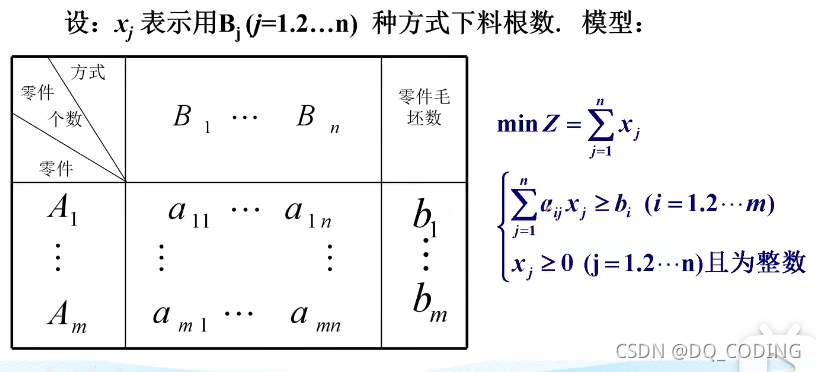
舉例-合理下料問題
模型:
題目:
這是在使用材料
1)使用零件A1-Am毛胚,就是使用零件
2)下料方式B1-Bn就是對零件進行操作
3)每種下料方式得到毛胚數(單種操作所需要的零件a11-amn)和每種零件的需要量(使用每種方式所需要滿足的零件總數量b1-bm)
解析:
1)對A1毛胚使用B1的下料方式需要的a11個零件個數(單個需求)
2)對A1使用B1-Bn種下料方式總共需要b1個零件數(總需求)
3)xj就是使用Bj的方式所需要使用的圓鋼數量
aijxj需要使用的零件數*圓鋼數>=bi要滿足的需求量
舉例-建廠問題
建表:
模型:
1)因為是否在Ai建廠關系著后續的計算,所以直接設置建廠為1,不建廠為0,這樣好進行運算
2)
Z:總建設費用和總運輸費用要最小
cijxij 運費運量=運輸的總費用
fi*yi建設費用x是否建廠=建廠總費用
3)
xij<=aiyi從工廠運輸出去的量必須小于工廠生產的產量
xij>=bj 運量必須大于等于銷量,滿足各地的需要
整數規劃的數學模型
xj取的是一個整數
bi 總數的限制,資源總量
分類:
詳細:
整數規劃與線性規劃的關系
線性規劃的最優解全為整數了,就可以作為ILP問題(線性規劃問題)的最優解,此時不再需要求導
整數規劃:決策變量為整數
說明:
