引入
線性規劃問題(松弛問題)

圖解法:
使用圖解法求出最優解,再使用四舍五入求出的整數解不滿足條件
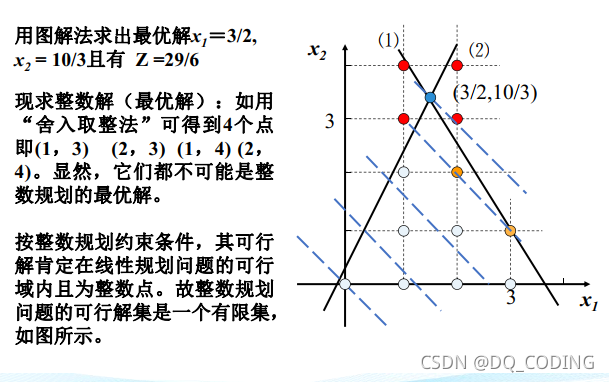
完全枚舉法(窮舉法):找出集合內所有滿足條件的整數點,再帶入不等式中,看是否有最優解
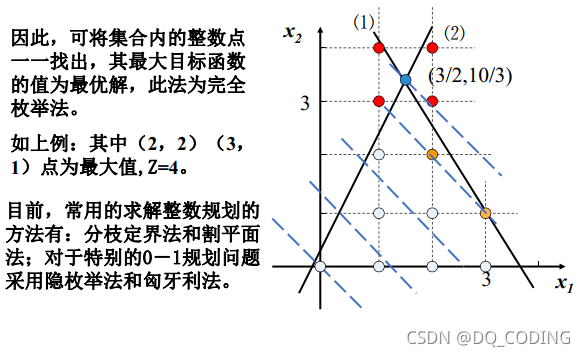
分支限界法
說明:
松弛問題:線性規劃問題
ILP:整數規劃,在線性規劃的基礎上對決策變量進行取整
所以線性規劃無可行解則整數規劃也無可行解
增加約束條件,一個個來,一次增加一個
對原始結果進行向上取整 [4.6]=5
對原始結果進行向下取整 [4.6]=4

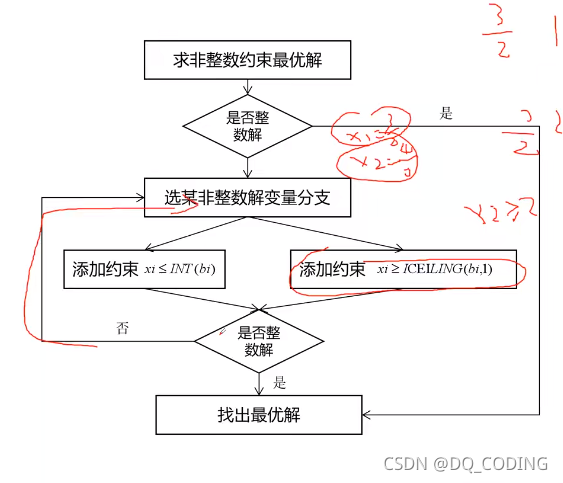
流程:
如果添加完約束之后仍然沒有找到整數解,那么此時分支限界法已經不能解決此問題了
案例
整數規劃的最優解只是針對決策變量x的,與目標值Z無關
所以x1=4;x2=1;z=14.3(是整數規劃的最優解)
1)當增加了x1<=3的條件之后,得出的結果中出現了非整數x2=2.67;所以此時還需要對x2向下取整與向上取整,看結果對比

判斷:
得到目標值高的先進行分支

matlab代碼
branchbound.m
function [newx,newfval,status,newbound] = branchbound(f,A,B,I,x,fval,bound,Aeq,Beq,lb,ub,e)% 分支定界法求解整數規劃
% f,A,B,Aeq,Beq,lb,ub與線性規劃相同
% I為整數限制變量的向量
% x為初始解,fval為初始值options = optimset('display','off');
[x0,fval0,status0]=linprog(f,A,B,Aeq,Beq,lb,ub,[],options);%遞歸中的最終退出條件
%無解或者解比現有上界大則返回原解
if status0 <= 0 || fval0 >= boundnewx = x;newfval = fval;newbound = bound;status = status0;return;
end%是否為整數解,如果是整數解則返回
intindex = find(abs(x0(I) - round(x0(I))) > e);
if isempty(intindex) %判斷是否為空值newx(I) = round(x0(I));newfval = fval0;newbound = fval0;status = 1;return;
end%當有非整可行解時,則進行分支求解
%此時必定會有整數解或空解
%找到第一個不滿足整數要求的變量
n = I(intindex(1));
addA = zeros(1,length(f));
addA(n) = 1;
%構造第一個分支 x<=floor(x(n))
A = [A;addA];
B = [B,floor(x(n))];%向下取整
[x1,fval1,status1,bound1] = branchbound(f,A,B,I,x0,fval0,bound,Aeq,Beq,lb,ub,e);
A(end,:) = [];
B(:,end) = [];
%解得第一個分支,若為更優解則替換,若不是則保持原狀status = status1;
if status1 > 0 && bound1 < boundnewx = x1;newfval = fval1;bound = fval1;newbound = bound1;
elsenewx = x0;newfval = fval0;newbound = bound;
end%構造第二分支
A = [A;-addA];
B = [B,-ceil(x(n))];%向上取整
[x2,fval2,status2,bound2] = branchbound(f,A,B,I,x0,fval0,bound,Aeq,Beq,lb,ub,e);
A(end,:) = [];
B(:,end) = [];%解得第二分支,并與第一分支做比較,如果更優則替換
if status2 > 0 && bound2 < boundstatus = status2;newx = x2;newfval = fval2;newbound = bound2;
endintprog.m
function [x,fval,status] = intprog(f,A,B,I,Aeq,Beq,lb,ub,e)
%整數規劃求解函數 intprog()
% 其中 f為目標函數向量
% A和B為不等式約束 Aeq與Beq為等式約束
% I為整數約束
% lb與ub分別為變量下界與上界
% x為最優解,fval為最優值
%例子:
% maximize 20 x1 + 10 x2
% S.T.
% 5 x1 + 4 x2 <=24
% 2 x1 + 5 x2 <=13
% x1, x2 >=0
% x1, x2是整數
% f=[-20, -10];
% A=[ 5 4; 2 5];
% B=[24; 13];
% lb=[0 0];
% ub=[inf inf];
% I=[1,2];
% e=0.000001;
% [x v s]= IP(f,A,B,I,[],[],lb,ub,,e)
% x = 4 1 v = -90.0000 s = 1% 控制輸入參數
if nargin < 9, e = 0.00001;if nargin < 8, ub = []; if nargin < 7, lb = []; if nargin < 6, Beq = []; if nargin < 5, Aeq = [];if nargin < 4, I = [1:length(f)];end, end, end, end, end, end%求解整數規劃對應的線性規劃,判斷是否有解
options = optimset('display','off');
[x0,fval0,exitflag] = linprog(f,A,B,Aeq,Beq,lb,ub,[],options);
if exitflag < 0disp('沒有合適整數解');x = x0;fval = fval0;status = exitflag;return;
else%采用分支定界法求解bound = inf;[x,fval,status] = branchbound(f,A,B,I,x0,fval0,bound,Aeq,Beq,lb,ub,e);
endtest.m
%例子1
% f = [-40 -90];%A = [9 7;7 20];%B = [56 70];
% lb = [0 0]';
%例子2f = [-20 -10];A = [5 4;2 5];B = [24 13];lb = [0 0];[x,fval,status] = intprog(f,A,B,[1 2],[],[],lb)

文件,并對原文件進行轉換)



元素方法詳解)












