狼羊人菜渡河問題

解答
試探法
因為有4個變量,所以一共有222*2=16種狀態
找出其中不安全的狀態:無人看守的狀態下:狼羊一起,羊菜一起
人 狼 羊 菜(0是在對面,1是在這邊)
狼羊一起:(0,1,1,0) (0,1,1,1) (1,0,0,0) (1,0,0,1)
羊菜一起:(0,0,1,1) (1,1,0,0)
其余的10個都是安全狀態

得到狀態轉移圖:證明是最優解
人1->0代表人渡河了,從此狀態到下一個狀態
(1,1,1,1)最開始的狀態->(0,1,0,1)人帶著羊一起渡河

商人過河問題

解答
模型建立
1)這時不能再使用(1,1,1,1,1,1)這種記錄狀態,有太多重復的,沒有必要,直接使用(商人人數,仆人人數)
2)因為當商人人數<仆人人數時,不安全,即有(1,2) (1,3) (2,3)這三種;但同時要同時保證這邊和對岸都是安全的,一邊不安全,這個狀態就是不安全的,所以,對應的(2,1) (2,0) (1,0)也是不安全狀態
3)所以一共有4*4=16-6=10種安全狀態

方法一:直觀法
使用x-y作圖,觀察可得路線,相當于下棋
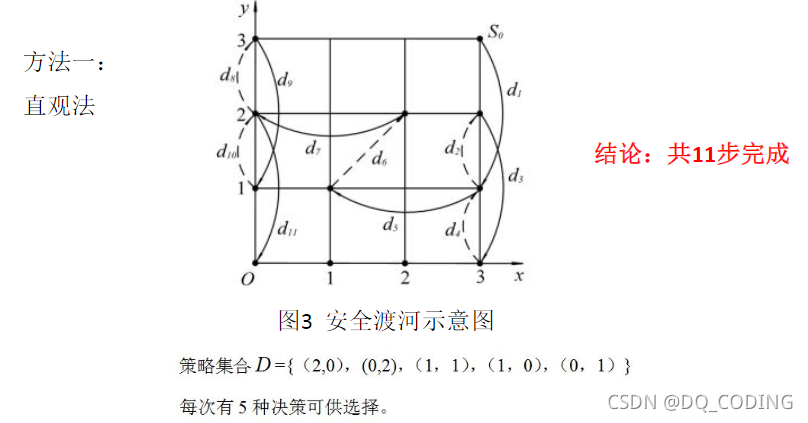
方法二:模型法
狀態轉移圖
(商人,仆人)加上一個船的狀態,就能進行狀態轉移(1次最多減少2個)
不能漏掉任何一條連線

等分酒問題

解答
注意:每次操作只有兩個瓶子,一個瓶子向另一個瓶子倒酒之后,下一步就不要再倒回來了,沒有必要且重復了
所以可以列出所有可能的操作結果

狀態轉移圖

棋子顏色問題

分析
1)在這里棋子的狀態不使用0,1;因為00=0,10=0不能從中判斷出棋子的顏色
2)所以需要進行變化的狀態,一般都可以考慮(a,-a)

舉例歸納:
多舉幾個列子(偶數,奇數),這樣才能看出規律
n=2時

n=3:
當a1^2=1時,可以直接省略掉(這就是省略偶數項)

n=4:

n=5:

結論

matlab程序
%:matlab注釋
x0=zeros(1,n):產生一個1行n列的矩陣,用來存放輸入數據-數組
x1=zeros(1,n):用來存放輸出結果-數組
for i=1:n從1到n開始循環
rand(1,1):1行1列(就是一個數),產生一個0-1之間的隨機實數
x0(i)=1:x0數組的第一個元素賦值為1
for k=1:n-1:對前面n-1個棋子進行操作(因為里面要用到k+1)

四人追逐問題
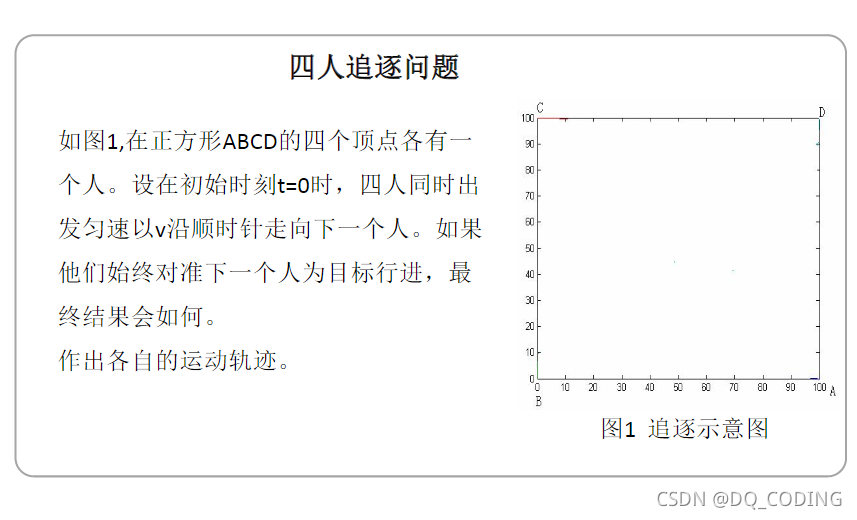
解答
1)順時針追逐,不是沿著正方形追逐,而是以對準下一個人的位置曲線的形式順時針方向追逐
2)運動軌跡是曲線,但在每一小段時間內,是一個直線(以曲化直的思維),所以此時求兩個人之間的距離直接變為了求直線距離
3)因為一個人追下一個人,所以追逐是兩個人的,假設每個人的坐標,使用三角公式就可以求得距離
4)因為最后是要求軌跡曲線,要作圖,所以直接使用在x和y兩個方向上的距離

表達式:

matlab程序
n=240;//總時刻,使用matlab多次測試看多少時刻時可以追上
x=zeros(4,n):4個人,240個時刻;x和y是使用兩個數組去記錄每個人x坐標和y坐標
dt=0.05;//從0開始每次增加0.05時刻,一直增加到240時刻追上了為止
v=10;//自己設定的速度

for j=1:n-1 1到n-1,因為要用到j+1
前三個人和最后一個人的公式不同,所以要分開寫
sqrt():計算平方根
x(i,j+1):計算每一個時刻的每個人的x坐標
vdtcosx:速度x時間間隔x在x方向上的距離(因為實際運動軌跡是曲線)
第四個人追第一個人:因為先寫的前三個人的運動代碼,所以,這里使用第一個人-第四個人
x(1,j) -x(4,j)

plot()繪圖,繪制每一個時刻每個人的位置
ro:紅色 bo藍色 go綠色 yo黃色
hold on 添加新繪圖時保存原有繪圖,這樣能把所有的點顯示在上面
pause(0.1)讓屏幕暫停0.1s,這樣能有逐步顯示的效果(動畫效果)
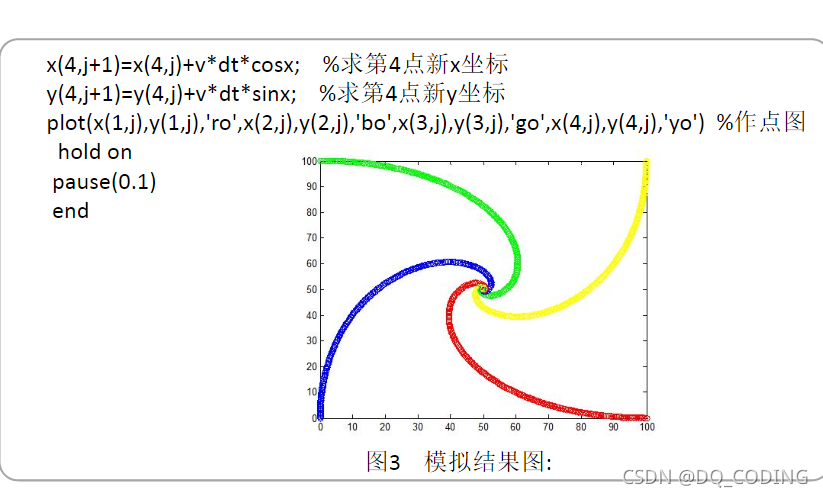
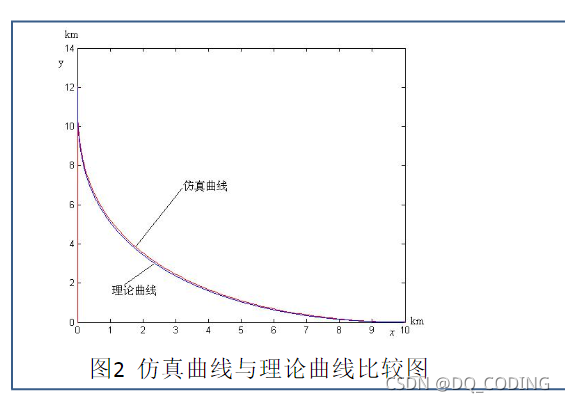
艦艇追擊問題

理論求解
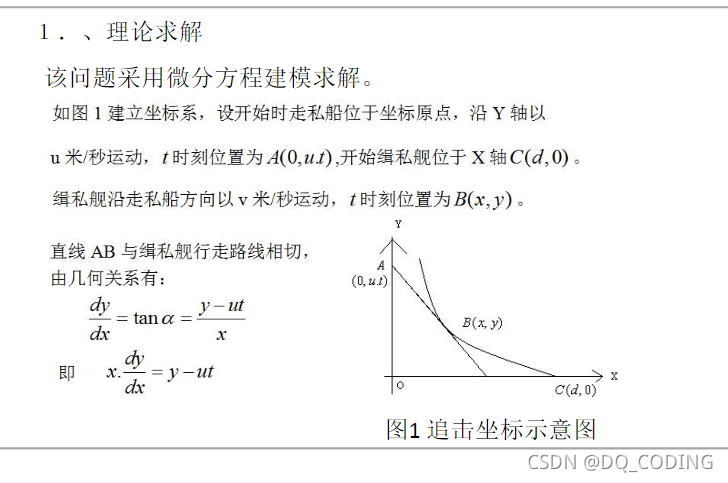


計算機模擬

matlab程序代碼







文件,并對原文件進行轉換)



元素方法詳解)









