redis——HyperLogLog

HyperLogLog 是一種概率數據結構，用來估算數據的基數。數據集可以是網站訪客的 IP 地址，E-mail 郵箱或者用戶 ID。

基數就是指一個集合中不同值的數目，比如 a, b, c, d 的基數就是 4，a, b, c, d, a 的基數還是 4。雖然 a 出現兩次，只會被計算一次。

使用 Redis 統計集合的基數一般有三種方法，分別是使用 Redis 的 HashMap，BitMap 和 HyperLogLog。前兩個數據結構在集合的數量級增長時，所消耗的內存會大大增加，但是 HyperLogLog 則不會。

Redis 的 HyperLogLog 通過犧牲準確率來減少內存空間的消耗，只需要12K內存，在標準誤差0.81%的前提下，能夠統計2^64個數據。所以 HyperLogLog 是否適合在比如統計日活月活此類的對精度要不不高的場景。

這是一個很驚人的結果，以如此小的內存來記錄如此大數量級的數據基數。下面我們就帶大家來深入了解一下 HyperLogLog 的使用，基礎原理，源碼實現和具體的試驗數據分析。

HyperLogLog 在 Redis 中的使用

Redis 提供了?PFADD?、?PFCOUNT?和?PFMERGE?三個命令來供用戶使用 HyperLogLog。

PFADD?用于向 HyperLogLog 添加元素。

> PFADD visitors alice bob carol(integer) 1> PFCOUNT visitors(integer) 3

如果 HyperLogLog 估計的近似基數在?PFADD?命令執行之后出現了變化，那么命令返回 1 ，否則返回 0 。如果命令執行時給定的鍵不存在，那么程序將先創建一個空的 HyperLogLog 結構，然后再執行命令。

PFCOUNT?命令會給出 HyperLogLog 包含的近似基數。在計算出基數后，?PFCOUNT?會將值存儲在 HyperLogLog 中進行緩存，知道下次?PFADD?執行成功前，就都不需要再次進行基數的計算。

PFMERGE?將多個 HyperLogLog 合并為一個 HyperLogLog ，合并后的 HyperLogLog 的基數接近于所有輸入 HyperLogLog 的并集基數。

> PFADD customers alice dan(integer) 1> PFMERGE everyone visitors customersOK> PFCOUNT everyone(integer) 4

內存消耗對比實驗

我們下面就來通過實驗真實對比一下下面三種數據結構的內存消耗，HashMap、BitMap 和 HyperLogLog。

我們首先使用 Lua 腳本向 Redis 對應的數據結構中插入一定數量的數，然后執行 bgsave 命令，最后使用 redis-rdb-tools 的 rdb 的命令查看各個鍵所占的內存大小。

下面是 Lua 的腳本

local key = KEYS[1]local size = tonumber(ARGV[1])local method = tonumber(ARGV[2])for i=1,size,1 doif (method == 0)thenredis.call('hset',key,i,1)elseif (method == 1)thenredis.call('pfadd',key, i)elseredis.call('setbit', key, i, 1)endend

我們在通過 redis-cli 的?script load?命令將 Lua 腳本加載到 Redis 中，然后使用?evalsha?命令分別向 HashMap、HyperLogLog 和 BitMap 三種數據結構中插入了一千萬個數，然后使用?rdb?命令查看各個結構內存消耗。

我們進行了兩輪實驗，分別插入一萬數字和一千萬數字，三種數據結構消耗的內存統計如下所示。

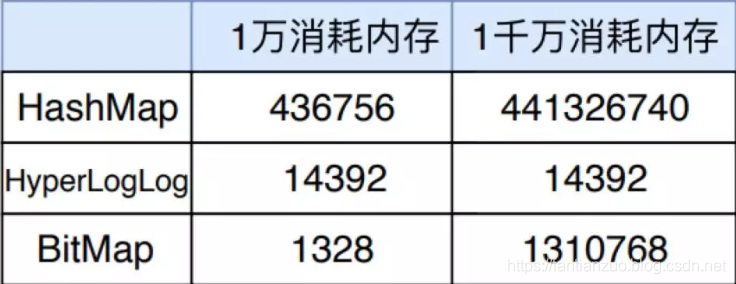
從表中可以明顯看出，一萬數量級時 BitMap 消耗內存最小，一千萬數量級時 HyperLogLog 消耗內存最小，但是總體來看，HyperLogLog 消耗的內存都是 14392 字節，可見 HyperLogLog 在內存消耗方面有自己的獨到之處。

基本原理

HyperLogLog 是一種概率數據結構，它使用概率算法來統計集合的近似基數。而它算法的最本源則是伯努利過程。

伯努利過程就是一個拋硬幣實驗的過程。拋一枚正常硬幣，落地可能是正面，也可能是反面，二者的概率都是 1/2 。伯努利過程就是一直拋硬幣，直到落地時出現正面位置，并記錄下拋擲次數k。比如說，拋一次硬幣就出現正面了，此時 k 為 1; 第一次拋硬幣是反面，則繼續拋，直到第三次才出現正面，此時 k 為 3。

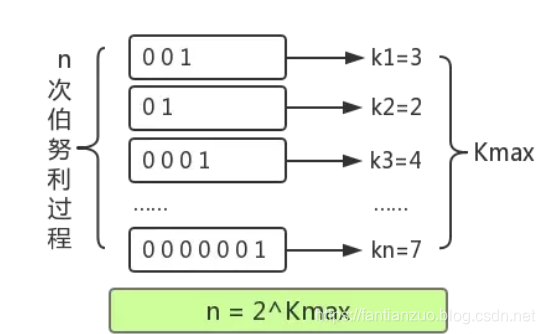
對于 n 次伯努利過程，我們會得到 n 個出現正面的投擲次數值 k1, k2 ... kn , 其中這里的最大值是k_max。

根據一頓數學推導，我們可以得出一個結論： 2^{k_ max} 來作為n的估計值。也就是說你可以根據最大投擲次數近似的推算出進行了幾次伯努利過程。

下面，我們就來講解一下 HyperLogLog 是如何模擬伯努利過程，并最終統計集合基數的。

HyperLogLog 在添加元素時，會通過Hash函數，將元素轉為64位比特串，例如輸入5，便轉為101(省略前面的0，下同)。這些比特串就類似于一次拋硬幣的伯努利過程。比特串中，0 代表了拋硬幣落地是反面，1 代表拋硬幣落地是正面，如果一個數據最終被轉化了 10010000，那么從低位往高位看，我們可以認為，這串比特串可以代表一次伯努利過程，首次出現 1 的位數為5，就是拋了5次才出現正面。

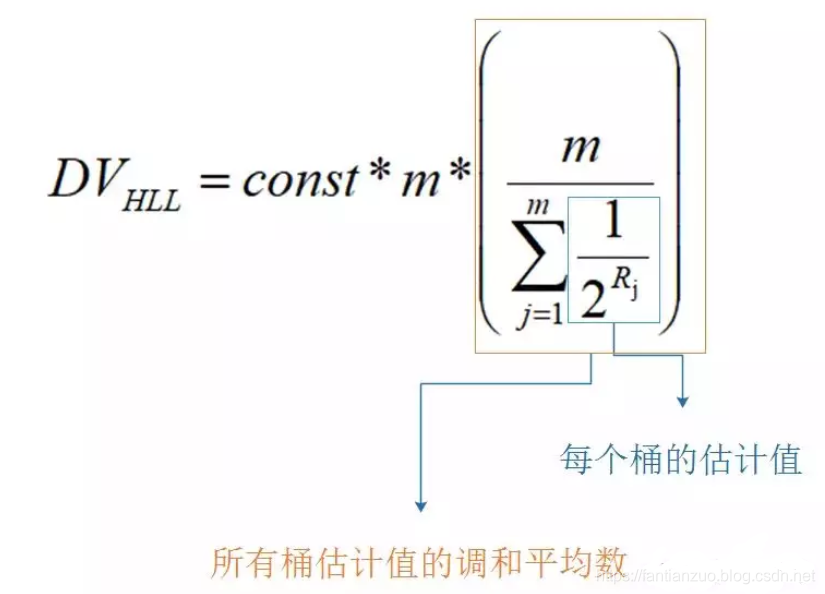
所以 HyperLogLog 的基本思想是利用集合中數字的比特串第一個 1 出現位置的最大值來預估整體基數，但是這種預估方法存在較大誤差，為了改善誤差情況，HyperLogLog中引入分桶平均的概念，計算 m 個桶的調和平均值。

Redis 中 HyperLogLog 一共分了 2^14 個桶，也就是 16384 個桶。每個桶中是一個 6 bit 的數組。

HyperLogLog 將上文所說的 64 位比特串的低 14 位單獨拿出，它的值就對應桶的序號，然后將剩下 50 位中第一次出現 1 的位置值設置到桶中。50位中出現1的位置值最大為50，所以每個桶中的 6 位數組正好可以表示該值。

在設置前，要設置進桶的值是否大于桶中的舊值，如果大于才進行設置，否則不進行設置。

此時為了性能考慮，是不會去統計當前的基數的，而是將 HyperLogLog 頭的 card 屬性中的標志位置為 1，表示下次進行 pfcount 操作的時候，當前的緩存值已經失效了，需要重新統計緩存值。在后面 pfcount 流程的時候，發現這個標記為失效，就會去重新統計新的基數，放入基數緩存。

在計算近似基數時，就分別計算每個桶中的值，帶入到上文的 DV 公式中，進行調和平均和結果修正，就能得到估算的基數值。

HyperLogLog 具體對象

我們首先來看一下 HyperLogLog 對象的定義

struct hllhdr {char magic[4]; /* 魔法值 "HYLL" */uint8_t encoding; /* 密集結構或者稀疏結構 HLL_DENSE or HLL_SPARSE. */uint8_t notused[3]; /* 保留位, 全為0. */uint8_t card[8]; /* 基數大小的緩存 */uint8_t registers[]; /* 數據字節數組 */};

HyperLogLog 對象中的?registers?數組就是桶，它有兩種存儲結構，分別為密集存儲結構和稀疏存儲結構，兩種結構只涉及存儲和桶的表現形式，從中我們可以看到 Redis 對節省內存極致地追求。

我們先看相對簡單的密集存儲結構，它也是十分的簡單明了，既然要有 2^14 個 6 bit的桶，那么我就真使用足夠多的?uint8_t?字節去表示，只是此時會涉及到字節位置和桶的轉換，因為字節有 8 位，而桶只需要 6 位。

所以我們需要將桶的序號轉換成對應的字節偏移量 offsetbytes 和其內部的位數偏移量 offsetbits。需要注意的是小端字節序，高位在右側，需要進行倒轉。

當 offset_bits 小于等于2時，說明一個桶就在該字節內，只需要進行倒轉就能得到桶的值。

?offset_bits 大于 2 ，則說明一個桶分布在兩個字節內，此時需要將兩個字節的內容都進行倒置，然后再進行拼接得到桶的值。

Redis 為了方便表達稀疏存儲，它將上面三種字節表示形式分別賦予了一條指令。