- 矩陣
SVD矩陣的乘法狀態轉移矩陣
狀態轉移矩陣 - 特征值和特征向量
對稱陣
正交陣
正定陣數據白化 - 矩陣求導
向量對向量求導
標量對向量求導
標量對矩陣求導
一.矩陣
1.1 SVD
奇異值分解(Singular Value Decomposition),假設A是一個m×n階矩陣,則存在一個分解使得

Σ對角線上的元素稱為矩陣A的奇異值;
U的第i列稱為A的關于σi的左奇異向量;
V的第i列稱為A的關于σi的右奇異向量。
通常將奇異值由大而小排列。如此Σ便能由M唯一確定了。(雖然U和V仍然不能確定)。而且奇異值的減少特別的快,在很多情況下,前10%甚至1%的奇異值的和就占了全部的奇異值之和的99%以上了。也就是說,我們也可以用前r大的奇異值來近似描述矩陣,那么SVD就起到一個特征選擇的作用或者是降維的作用。
具體描述參考:http://blog.csdn.net/zhongkejingwang/article/details/43053513
1.2 代數余子式![]()
在一個n階行列式A中,把(i,j)元素aij所在的第i 行和第j列劃去后,留下的n-1階方陣的行列式叫做元素aij的余子式,記作Mij
注意:行列式是數值,因此余子式和代數余子式也是數值;余子式可能也可能是負數。
?
1.3 伴隨矩陣

注意:![]() 位于
位于![]() 第j行i列
第j行i列
?
1.4? 方陣的逆
![]()
當方陣的行列式不為0時,有:![]()
如果不是方正,請參考矩陣的廣義逆
?
1.5 范德蒙行列式

1.6 矩陣的乘法
為階的矩陣,為階的矩陣,那么,是階的矩陣,其中
1.7 矩陣和向量的乘法
- 為階的矩陣,為階的矩陣,則 為的列向量,記
- 由于維列向量和n維空間的點一一對應,上式實際給出了從維空間的點到維空間的的線性變換。
- 旋轉、平移
1.8 狀態轉移矩陣
數學解釋:
設一個初始概率分布(只是一個向量)
- 第代中處于第個階層的概率為:
原理:全概率公式:?參考馬爾科夫過程:https://blog.csdn.net/u010459100/article/details/51657955
1.9.矩陣的秩
- 在的矩陣A中,任取行列,不改變這個元素在中的次序,得到階方陣,稱為矩陣的k階子式。
- 設在矩陣A中有一個
不等于的階子式,且所有階子式全等于(如果存在的話),那么稱為矩陣的最高階非零子式,稱為矩陣的秩,記作
- 如果一個矩陣那么可以說這個矩陣式滿秩的
- 的可逆矩陣,秩為n
矩陣的秩等于它的行列向量組的秩
1.91 秩和線性方程組的解的關系
對于n元線性方程組Ax = b:
- 無解的充要條件是
- 唯一解的充要條件是
- Ax= 0的只有零解的充要條件是
- 無窮解的充要條件是
- Ax= b有解的充要條件是
- Ax= 0的非零解的充要條件是
1.10向量組
向量b能由向量組線性表示的充
要條件是矩陣的秩等于矩陣
的秩。
因為有解的條件是秩相等。
=
- 若向量組A與向量組B能相互線性表示,則稱兩個向量組等價。
1.11系數矩陣
參考:https://blog.csdn.net/IOThouzhuo/article/details/50836787二.特征值和特征向量2.1正交陣
- 若階矩陣A滿足,稱A為正交矩陣,簡稱正交陣。
- 是正交陣的充要條件:A的列(行)向量都是單位向量,且兩兩正交。
- 是正交陣,X為向量,則Ax稱作正交變換。
- 正交變換不改變向量長度。
2.2特征值和特征向量
A是n階矩陣,若數和n維非0列向量滿足,那么,數稱為A的特征向值,x稱為A的對應于特征值的特征向量。
- 根據定義,立刻得到,令關于的多項式為0,方程的根為的特征值;將根帶入方程組,求得到的非零解,即對應的特征向量。
- 設階矩陣的特征值為,則
- 矩陣A的主行列式的元素和,稱作矩陣A的跡?
推論:
不同特征值對應的特征向量,線性無關。
實對稱陣的特征值也是實數。
實對稱陣不同的特征值的特征向量正交
2.3 合同變換
設A為n階對稱陣,則必有正交陣P,使得
2.4.正定陣
對于階方陣,若任意階向量,都有,則稱是正定陣。
- 由一階推廣而來:
- 若條件變成,則稱作半正定矩陣。
正定陣的判定:
- 對稱陣A為正定陣;
- A的特征值都為正;
- A的順序主子式大于0;
2.5 漂白/白化whitening
暫定
三. 矩陣求導

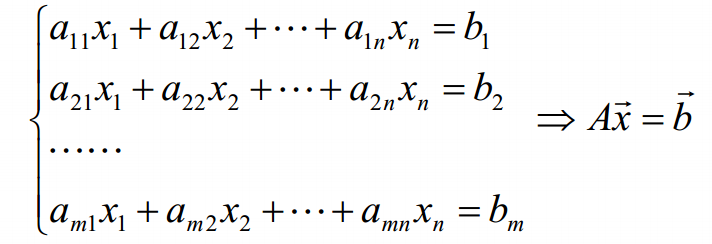
提煉)



-網-ifconfig,ping,ssh)


--Brightness Controller)


-資源-du,top,free,gnome)

-遠程登入服務器)


)
-配置pytorch)
)

-MySQLdb)