13.1 距離度量

• 距離函數種類：歐式距離、曼哈頓距離、明式距離（閔可夫斯基距離）、馬氏距離、切比雪夫距離、標準化歐式距離、漢明距離、夾角余弦等
• 常用距離函數：歐式距離、馬氏距離、曼哈頓距離、明式距離
  1.歐式距離
  歐式距離是最容易直觀理解的距離度量方法，我們小學，中學，高中所接觸的兩個空間中的距離一般都是指的是歐式距離。
  
  2.曼哈頓距離(Manhattan Distance)
  兩個點在標準坐標系上的絕對軸距總和
  
  3.切比雪夫距離
  各坐標數值差的最大值
  
  4.閔可夫斯基距離
  閔氏距離不是一種距離，而是一組距離的定義，是對多個距離度量公式的概括性的表述。
  
  5.標準化歐氏距離
  定義： 標準化歐氏距離是針對歐氏距離的缺點而作的一種改進。標準歐氏距離的思路：既然數據各維分量的分布不一樣，那先將各個分量都**“標準化”**到均值、方差相等。
  
  6.馬氏距離
  **概念：**馬氏距離是基于樣本分布的一種距離。物理意義就是在規范化的主成分空間中的歐氏距離。所謂規范化的主成分空間就是利用主成分分析對一些數據進行主成分分解。再對所有主成分分解軸做歸一化，形成新的坐標軸。由這些坐標軸張成的空間就是規范化的主成分空間。
  
  馬氏距離的優點：與量綱無關，排除變量之間的相關性干擾
  7.余弦距離
  
  夾角余弦取值范圍為[-1,1]。余弦越大表示兩個向量的夾角越小，余弦越小表示兩向量的夾角越大。當兩個向量的方向重合時余弦取最大值1，當兩個向量的方向完全相反余弦取最小值-1。
  8.漢明距離
  定義：兩個等長字符串s1與s2的漢明距離為：將其中一個變為另外一個所需要作的最小字符替換次數。
  9.信息熵
  以上的距離度量方法度量的皆為兩個樣本（向量）之間的距離，而信息熵描述的是整個系統內部樣本之間的一個距離，或者稱之為系統內樣本分布的集中程度（一致程度）、分散程度、混亂程度（不一致程度）。系統內樣本分布越分散(或者說分布越平均)，信息熵就越大。分布越有序（或者說分布越集中），信息熵就越小。
  

13.2 損失函數

• log對數 損失函數（邏輯回歸）
• 平方損失函數（最小二乘法）
• 指數損失函數（AdaBoost）
• Hinge損失函數（SVM）
• 0-1損失函數
• 絕對值損失函數
  損失函數（loss function）是用來估量你模型的預測值f(x)與真實值Y的不一致程度，它是一個非負實值函數,通常使用L(Y, f(x))來表示，損失函數越小，模型的魯棒性就越好。
  損失函數是經驗風險函數的核心部分，也是結構風險函數重要組成部分。模型的結構風險函數包括了經驗風險項和正則項
  1.log對數 損失函數
  在邏輯回歸的推導中，它假設樣本服從伯努利分布（0-1分布），然后求得滿足該分布的似然函數。
  log函數是單調遞增的，（凸函數避免局部最優）
  在使用梯度下降來求最優解的時候，它的迭代式子與平方損失求導后的式子非常相似
  2.平方損失函數（最小二乘法, Ordinary Least Squares）
  最小二乘法是線性回歸的一種，OLS將問題轉化成了一個凸優化問題。
  在線性回歸中，它假設樣本和噪聲都服從高斯分布（為什么假設成高斯分布呢？其實這里隱藏了一個小知識點，就是中心極限定理），最后通過極大似然估計（MLE）可以推導出最小二乘式子。
  為什么它會選擇使用歐式距離作為誤差度量呢（即Mean squared error， MSE），主要有以下幾個原因：
• 簡單，計算方便；
• 歐氏距離是一種很好的相似性度量標準；
• 在不同的表示域變換后特征性質不變
  3.指數損失函數（AdaBoost）
  
  4.hinge損失
  在機器學習算法中，hinge損失函數和SVM是息息相關的。在線性支持向量機中，最優化問題可以等價于下列式子：
  
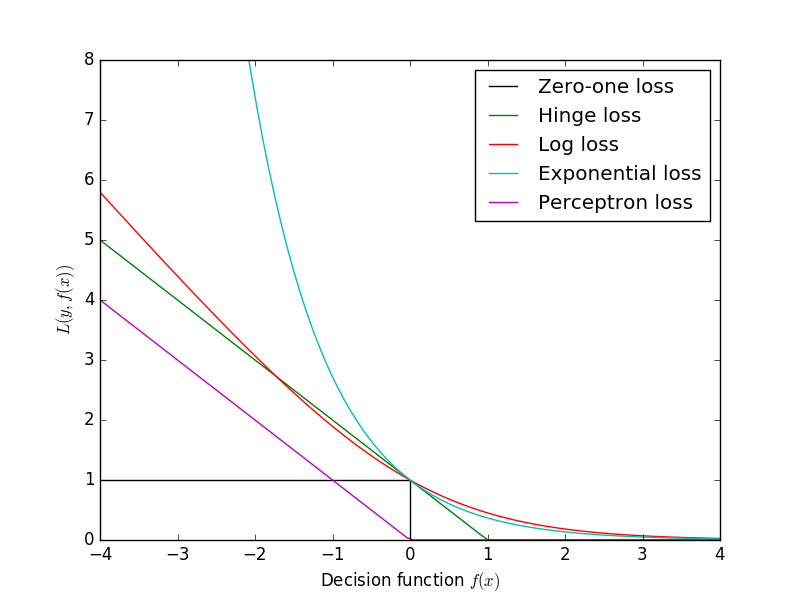
  損失函數總結