幾乎所有的的機器學習問題最終都將轉換為一個最優化問題，而一般回轉換為最小化問題
傳統的解析方法在機器學習的優化問題中常常不適用，通常使用的是迭代優化的問題，需要確定兩個關鍵點：1.下降的方向 2.確定下降的步長
參考博客

1.梯度下降

每次都沿著目標函數的負梯度方向進行下降，更新參數

1.1批量梯度下降(BGD)

BGD 采用整個訓練集的數據來計算 cost function 對參數的梯度

1.2隨機梯度下降（SGD）

和批量梯度下降(BGD) 的一次用所有數據計算梯度相比，隨機梯度下降(SGD)每次更新時對每個樣本進行梯度更新，
對于很大的數據集來說，可能會有相似的樣本，這樣 BGD 在計算梯度時會出現冗余， 而 SGD 一次只進行一次更新，
就沒有冗余，而且比較快，并且可以新增樣本。

缺點
隨機梯度下降(SGD)因為更新比較頻繁，會造成 cost function 有嚴重的震蕩，此外隨機梯度下降(SGD)對噪聲比較敏感；批量梯度下降(BGD)可以收斂到局部極小值，當然 隨機梯度下降(SGD)的震蕩可能會跳到更好的局部極小值處。；當我們稍微減小 learning rate，隨機梯度下降(SGD)和批量梯度下降(BGD)的收斂性是一樣的。

1.3 小批量隨機梯度下降（MSGD）

MBGD 每一次利用一小批樣本，即 n 個樣本進行計算， 這樣它可以降低參數更新時的方差，收斂更穩定，

另一方面可以充分地利用深度學習庫中高度優化的矩陣操作來進行更有效的梯度計算。
和 SGD 的區別是每一次循環不是作用于每個樣本，而是具有 n 個樣本的Batch。

缺點

• 1.選擇合適的學習率非常困難。太大會使得手斂波動大，太小使得手斂速度慢
• 2.所有的參數使用相同的學習率。對于不經常出現的特征的參數希望更新快些，對于常常出現的特征則希望跟新慢一些
• 3.sgd容易收斂到局部最優解，并且在某些會受到鞍點影響；通過合適的初始化和step size設置下，鞍點影響可以降低。

minibatchSGD是梯度下降方法中較常用的方法，而且性能比其他兩種都要好一些。但是仍然存在很多的問題，于是就有后面的那些改進的方法。

1.4 比較：

1.5 動量算法（momentum）

1.6 Nestrov Momentum

2. 自適應方法

2.1 自適應學習率算法（AdaGrad）

2.2 均方根反向傳播算法(RMSprop)

2.3 Adadelta

2.4 自適應矩估計優化算法(Adam)

3.牛頓法

3.1 牛頓法

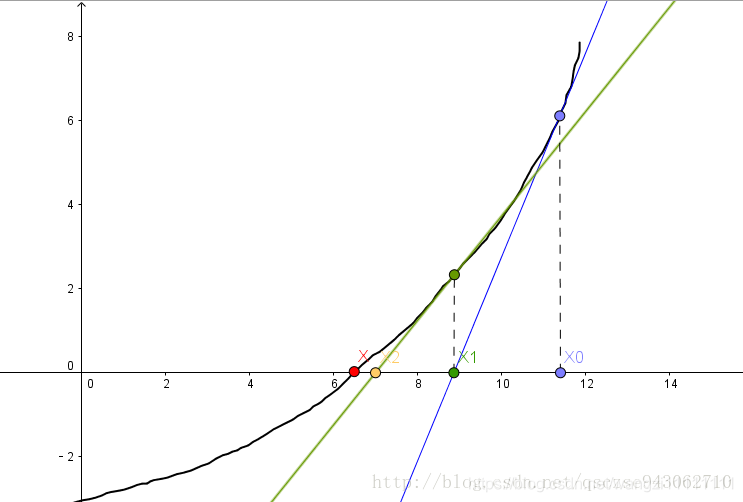
3.2 擬牛頓法

總結