目錄

搜索二叉樹的性質

搜索二叉樹的實現、

插入

?刪除

?代碼

---

在以前我們學過二叉樹,但是在對二叉樹的學習中發現,似乎二叉樹并沒有什么作用,要論增刪它比不上鏈表,論隨機訪問也沒法和順序表比,對于當時的我們是一頭霧水,那么現在它的功能終于是體現出來了,這里就是我們要講的搜索二叉樹。

搜索二叉樹的性質

在這里我們先了解一下什么是搜索二叉樹，搜索二叉樹，顧名思義它要滿足搜索的特征，于是就有人想出來一個辦法，我能不能在創建一個樹的時候，比它小的值放在左子樹，比它大的值放在右子樹呢，這樣的話當我們要去尋找某一個節點的時候，只需要比較一下左右子樹，如果這個值大就往它的右邊走，比它小就往它的左邊走呢。

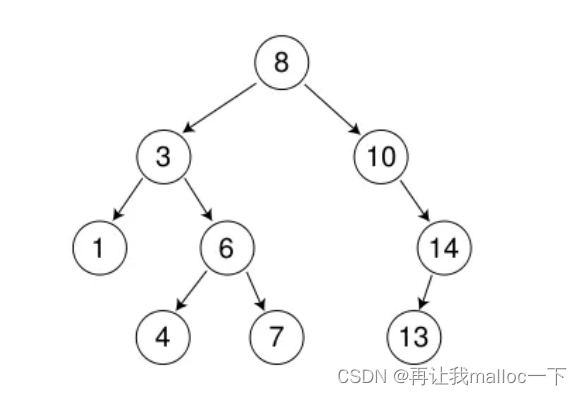
?比如這里就是我們的一顆搜索二叉樹，當我們要去尋找一個值為6的時候，我就可以先和它的根節點比，小走左邊，大走右邊。

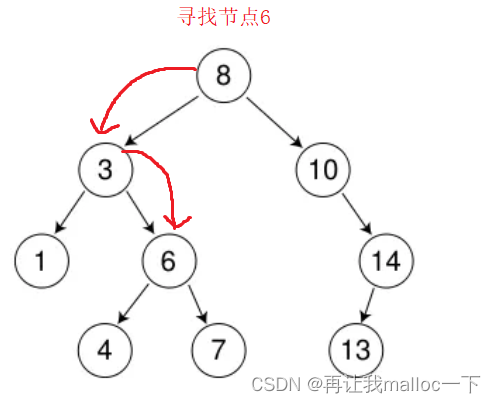
?按照這個特性，只要一顆搜索二叉樹被建立出來了，那么想要尋找一個值是不是時間效率非常的高？答案是否的，在某一個情況下我們想要尋找一個節點消耗的時間也是非常困難的

?比如說是這樣的一個搜索二叉樹，它在圖形上有點像我們的單鏈表，這樣的一棵樹如果要去尋找某個節點值的時候效率也是會達到o(N)的。

如果我們在仔細觀察一下的話，會發現如果我們對這課樹走一個中序遍歷的話得到的值會是一個有序的。例如這棵樹，如果中序走出來就是

1->3->4->6->7->8->10->13->14

所以我們現在知道二叉樹的特性大概有

它的左子樹必須是比根節點要小的

它的右子樹必須是比根節點要大的

它的中序遍歷一定是有序的

搜索二叉樹的實現、

插入

要創建一顆二叉樹，那么我們在插入數據的時候就要按照二叉樹的特征來進行插入，創建很簡單，只需要依次尋找，比它小往左，比它大往右，知道找到為空的那個未知就是我們需要插入的值，但是會有一個問題，找到當前為空的時候直接插入并沒有把當前節點和這顆樹聯系起來，所以還要記錄一下它的父親節點。但是這里我們用另一種思路，那么就是傳入的時候用引用，這樣下一個節點就是上一個節點的引用，給當前節點賦值實際是給上一個節點的左右子樹來賦值

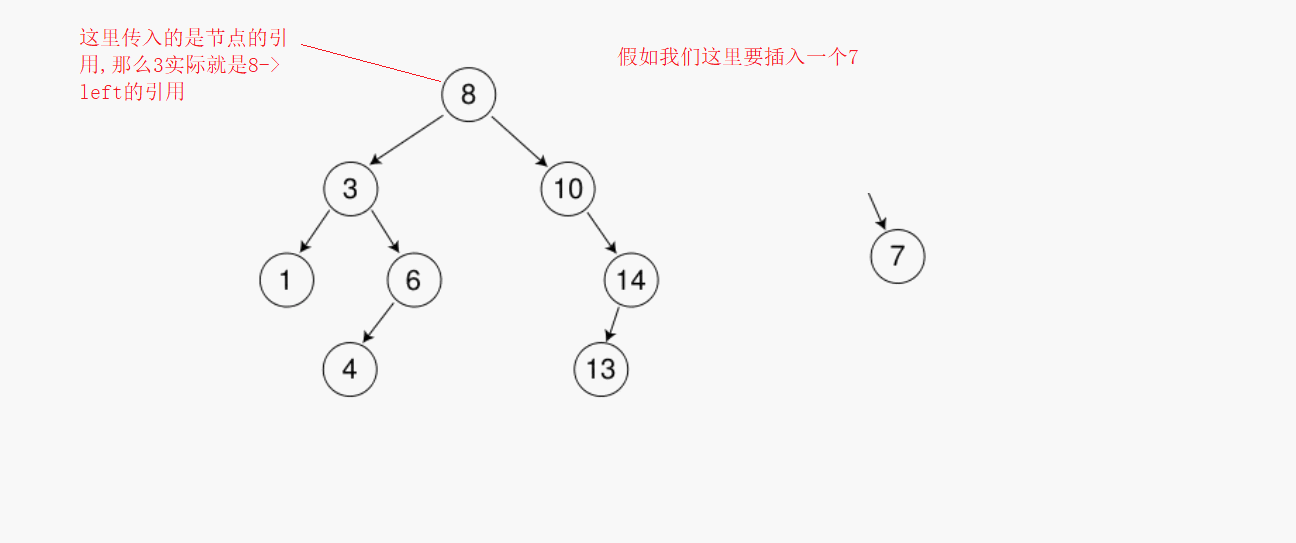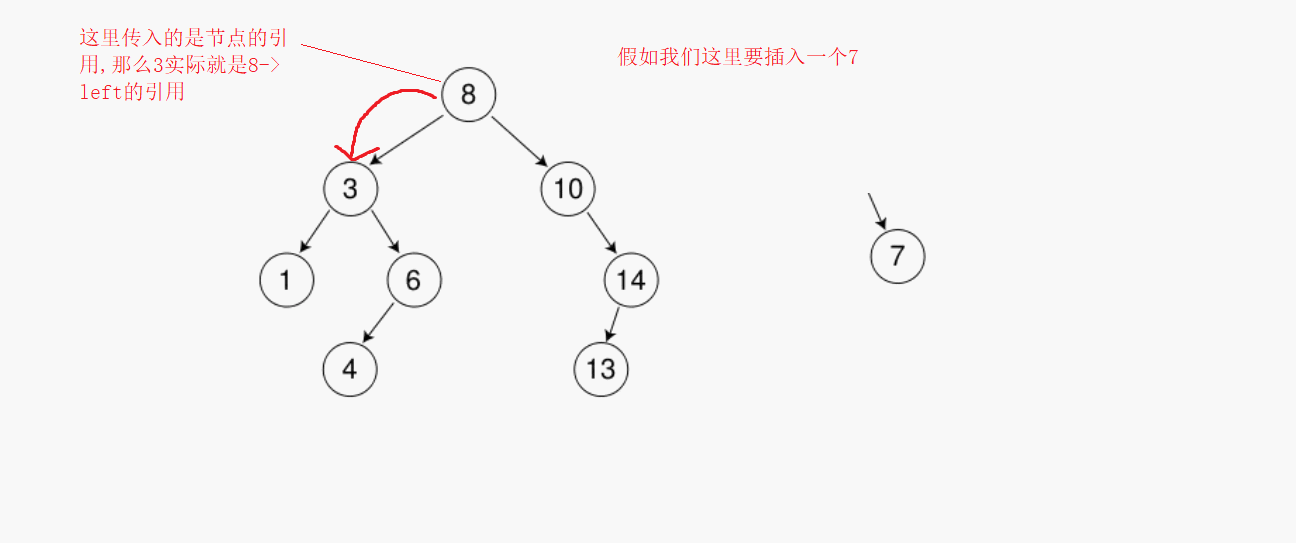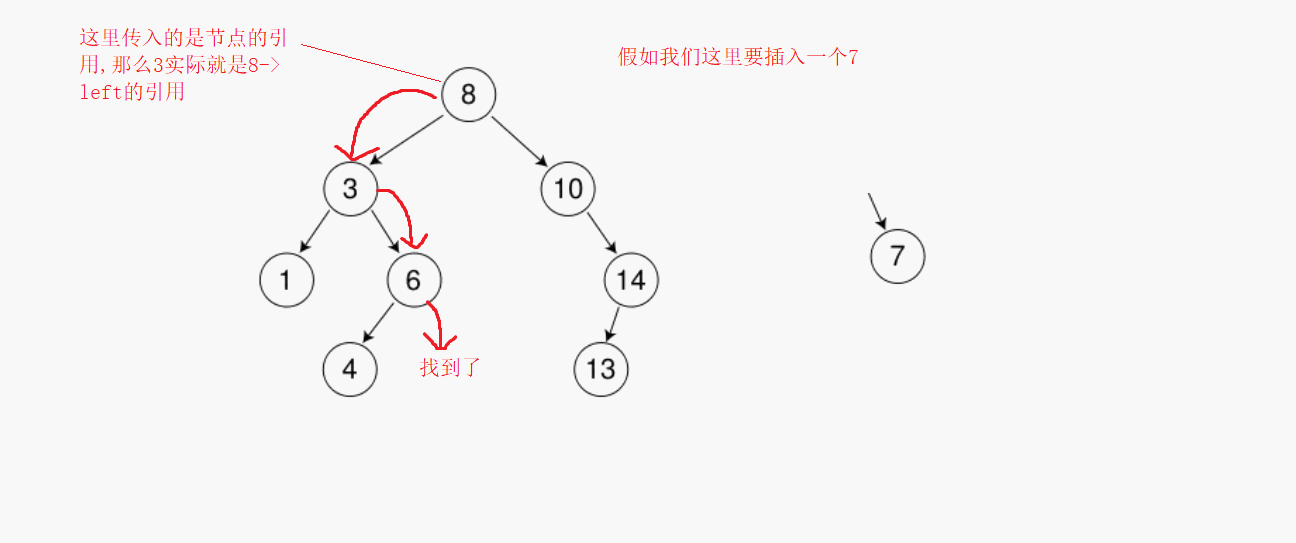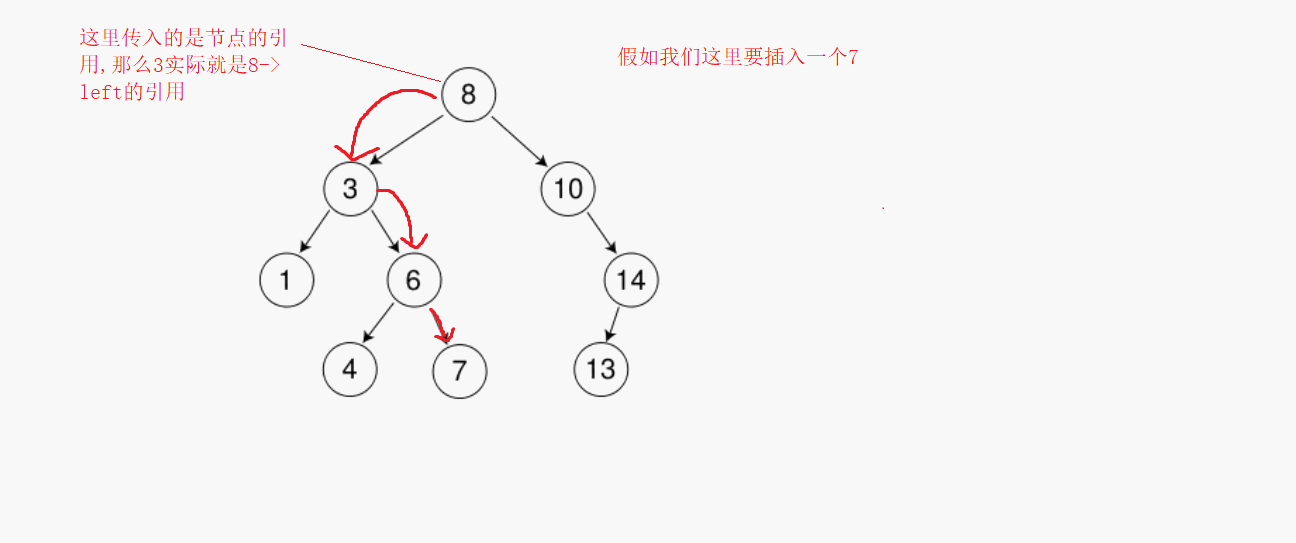
?刪除

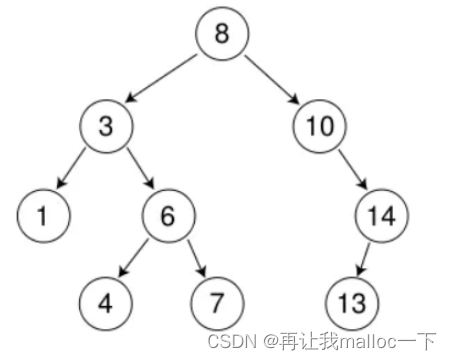
插入看出來其實很簡單，這里難的是我們的刪除。要刪除一個結點可能會遇到四種情況

a. 要刪除的結點無孩子結點
b. 要刪除的結點只有左孩子結點
c. 要刪除的結點只有右孩子結點
d. 要刪除的結點有左、右孩子結點
?

如果要刪除的是葉子結點，那么可以直接刪除，如果要刪除有左孩子就要考慮如果講左孩子鏈接道父親結點，如果是有右孩子就要考慮如果講右孩子鏈接上去。如果左右孩子都有這里就要考慮另一種方法替換法。

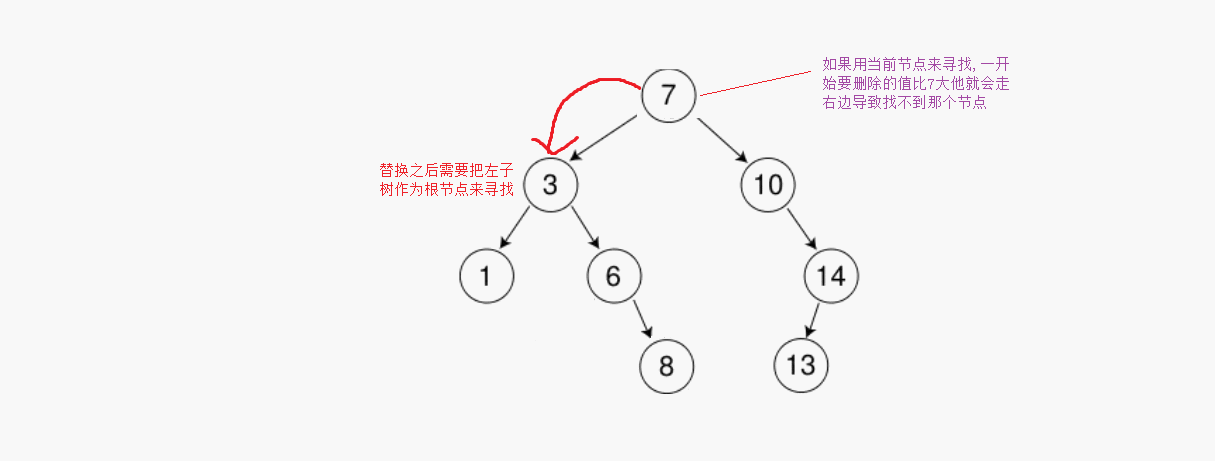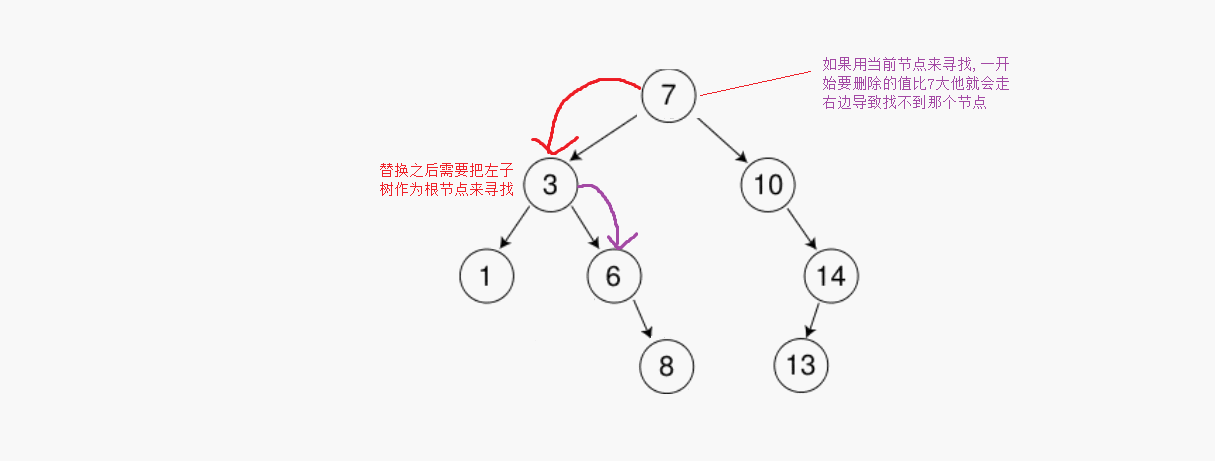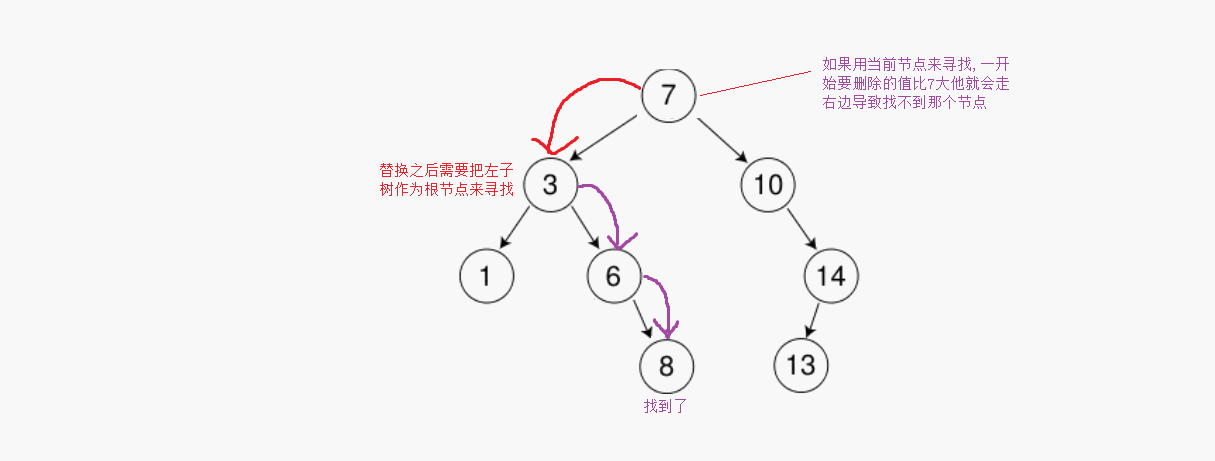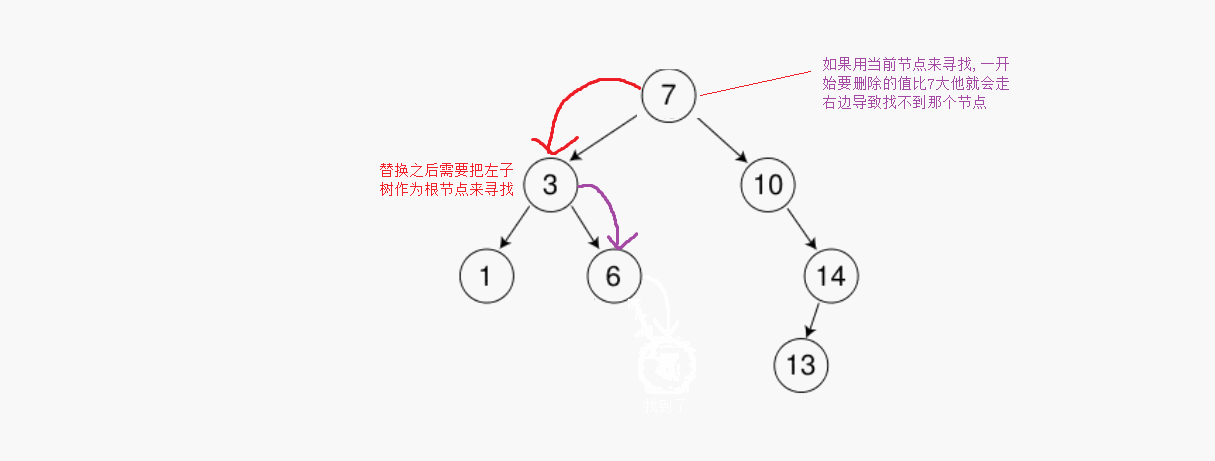
那么什么是替換法，這里加入我們需要刪除的節點為8，那么我們可以選擇讓左子樹最大的節點來替代它。

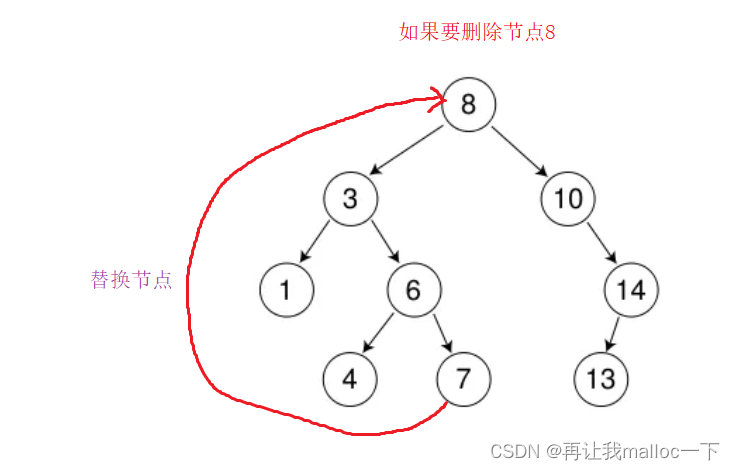
?這里還要注意一個問題，當我們用左子樹最大的機電替換之后需要從左子樹的第一個節點作為根節點開始尋找，如果用第一個節點來尋找的話第一次比較比當前節點大會往右邊走，最后導致找不到這個節點

?代碼

#pragma once
#include<iostream>using namespace std;template<class K>
struct BSNode
{BSNode* _left;BSNode* _right;K _key;BSNode(const K& key):_left(nullptr),_right(nullptr),_key(key){}
};template<class K>
class BSTree
{
public:typedef BSNode<K> Node;BSTree():_root(nullptr){}BSTree(const BSTree<int>& t){_root = _copy(t._root);}bool FindR(const K& key){return _FindR(_root,key);}bool Insert(const K& key){return _Insert(_root, key);}void Inorder(){_Inorder(_root);}bool erase(const K& key){return _erase(_root, key);}~BSTree(){destor(_root);}
private:Node* _copy(const Node* t){if (t == nullptr)return nullptr;Node* copynode = new Node(t->_key);copynode->_left = _copy(t->_left);copynode->_right = _copy(t->_right);return copynode;}bool _Insert(Node*& root,const K& key){if (root == nullptr){root = new Node(key);		//這里可以直接這樣插入是因為當前結點是root-左右指向的引用return true;}//開始往左右兩邊去找插入的未知if (root->_key < key){return _Insert(root->_right,key);	}else if (root->_key > key){return _Insert(root->_left, key);}else{return false;}}bool _erase(Node*& root, const K& key){if (root == nullptr)		//先判斷是否為空樹return false;if (root->_key < key)	//如果要刪除的值比當前節點大{	return _erase(root->_right,key);	//開始往右邊遞歸}else if (root->_key > key)	//如果要刪除的值比當前節點小{return _erase(root->_left,key);	//開始往左邊遞歸}else{//刪除有左或右孩子的情況if (root->_left == nullptr)	//如果它的左子樹為空{root = root->_right;	//那么就讓它的右節點等于當前節點}else if (root->_right == nullptr)//如果它的右子樹為空{root = root->_left;//那么就讓它的左節點等于當前節點}//左右都有孩子的情況else{Node* del = root;Node* leftMax = root->_left;	while (leftMax->_right){leftMax = leftMax->_right;	//用左孩子最大的節點來替換當前要刪除的節點}swap(root->_key, leftMax->_key);_erase(root->_left, key);	//這里不能從第一個節點開始找,因為當前樹的節點已經被替換過了,如果從第一個節點開始找會導致找不到這個節點del = leftMax;	delete del;	//找到之后刪除當前節點return true;}}}bool _FindR(const Node* root,const K& key){if (root == nullptr)return false;if (root->_key < key){return _FindR(root->_right);}else if (root->_key > key){return _FindR(root->_left);}else{return true;}}void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_key << " ";_Inorder(root->_right);}void destor(Node* root){if (root == nullptr)return;destor(root->_left);destor(root->_right);delete root;root = nullptr;}Node* _root;
};//測試#pragma once#include"RecursiveBinarySearchTree.h"
using namespace std;int main()
{int arr[] = { 8,3,10,1,6,14,4,7,13 };BSTree<int> t;for (auto e : arr){t.Insert(e);}t.Inorder();t.erase(6);t.erase(1);t.erase(8);t.erase(13);cout << endl;t.Inorder();cout << endl;BSTree<int> t1(t);t1.Inorder();return 0;
}