目錄
回溯算法詳解
回溯VS遞歸
回溯算法的實現過程
n個結點構造多本節要討論的是當給定 n(n>=0)個結點時,可以構建多少種形態不同的樹。
回溯算法詳解
回溯算法,又稱為“試探法”。解決問題時,每進行一步,都是抱著試試看的態度,如果發現當前選擇并不是最好的,或者這么走下去肯定達不到目標,立刻做回退操作重新選擇。這種走不通就回退再走的方法就是回溯算法。
例如,在解決列舉集合 {1,2,3} 中所有子集的問題中,就可以使用回溯算法。從集合的開頭元素開始,對每個元素都有兩種選擇:取還是舍。當確定了一個元素的取舍之后,再進行下一個元素,直到集合最后一個元素。其中的每個操作都可以看作是一次嘗試,每次嘗試都可以得出一個結果。將得到的結果綜合起來,就是集合的所有子集。
實現代碼為:
- #include <stdio.h>
- //設置一個數組,數組的下標表示集合中的元素,所以數組只用下標為1,2,3的空間
- int set[5];
- //i代表數組下標,n表示集合中最大的元素值
- void PowerSet(int i,int n){
- //當i>n時,說明集合中所有的元素都做了選擇,開始判斷
- if (i>n) {
- for (int j=1; j<=n; j++) {
- //如果樹組中存放的是 1,說明在當初嘗試時,選擇取該元素,即對應的數組下標,所以,可以輸出
- if (set[j]==1) {
- printf("%d ",j);
- }
- }
- printf("\n");
- }else{
- //如果選擇要該元素,對應的數組單元中賦值為1;反之,賦值為0。然后繼續向下探索
- set[i]=1;PowerSet(i+1, n);
- set[i]=0;PowerSet(i+1, n);
- }
- }
- int main() {
- int n=3;
- for (int i=0; i<5; i++) {
- set[i]=0;
- }
- PowerSet(1, n);
- return 0;
- }
運行結果:
1 2 3
1 2
1 3
1
2 3
2
3
回溯VS遞歸
很多人認為回溯和遞歸是一樣的,其實不然。在回溯法中可以看到有遞歸的身影,但是兩者是有區別的。
回溯法從問題本身出發,尋找可能實現的所有情況。和窮舉法的思想相近,不同在于窮舉法是將所有的情況都列舉出來以后再一一篩選,而回溯法在列舉過程如果發現當前情況根本不可能存在,就停止后續的所有工作,返回上一步進行新的嘗試。
遞歸是從問題的結果出發,例如求 n!,要想知道 n!的結果,就需要知道 n*(n-1)! 的結果,而要想知道 (n-1)! 結果,就需要提前知道 (n-1)*(n-2)!。這樣不斷地向自己提問,不斷地調用自己的思想就是遞歸。
回溯和遞歸唯一的聯系就是,回溯法可以用遞歸思想實現。
回溯算法的實現過程
使用回溯法解決問題的過程,實際上是建立一棵“狀態樹”的過程。例如,在解決列舉集合{1,2,3}所有子集的問題中,對于每個元素,都有兩種狀態,取還是舍,所以構建的狀態樹為:
?
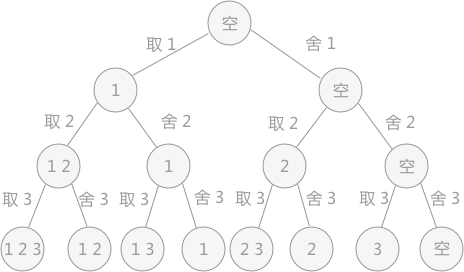
圖1 狀態樹
回溯算法的求解過程實質上是先序遍歷“狀態樹”的過程。樹中每一個葉子結點,都有可能是問題的答案。圖 1 中的狀態樹是滿二叉樹,得到的葉子結點全部都是問題的解。
在某些情況下,回溯算法解決問題的過程中創建的狀態樹并不都是滿二叉樹,因為在試探的過程中,有時會發現此種情況下,再往下進行沒有意義,所以會放棄這條死路,回溯到上一步。在樹中的體現,就是在樹的最后一層不是滿的,即不是滿二叉樹,需要自己判斷哪些葉子結點代表的是正確的結果。
n個結點構造多本節要討論的是當給定 n(n>=0)個結點時,可以構建多少種形態不同的樹。
如果兩棵樹中各個結點的位置都一一對應,可以說這兩棵樹相似。如果兩棵樹不僅相似,而且對應結點上的數據也相同,就可以說這兩棵樹等價。本節中,形態不同的樹指的是互不相似的樹。
前面介紹過,對于任意一棵普通樹,通過孩子兄弟表示法的轉化,都可以找到唯一的一棵二叉樹與之對應。所以本節研究的題目也可以轉化成:n 個結點可以構建多少種形態不同的二叉樹。
每一棵普通樹對應的都是一棵沒有右子樹的二叉樹,所以對于 n 個結點的樹來說,樹的形態改變是因為除了根結點之外的其它結點改變形態得到的,所以,n 個結點構建的形態不同的樹與之對應的是 n-1 個結點構建的形態不同的二叉樹。
如果 tn?表示 n 個結點構建的形態不同的樹的數量,bn?表示 n 個結點構建的形態不同的二叉樹的數量,則兩者之間有這樣的關系:tn=bn-1。
【方法一】
最直接的一種方法就是推理。當 n=0 時,只能構建一棵空樹;當 n=2 時,可以構建 2 棵形態不同的二叉樹,如圖 1(A);當 n=3 時,可以構建 5 棵形態互不相同的二叉樹,如圖 1(B)。
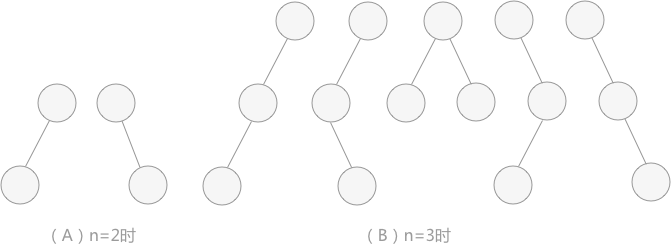
圖 1 不同形態的二叉樹
對于具有 n( n>1 )個結點的二叉樹來說,都可以看成是一個根結點、由 i 個結點組成的左子樹和由?n-i-1?個結點組成的右子樹。
當 n=1 時,也適用,只不過只有一個根結點,沒有左右孩子(i=0)。
可以得出一個遞推公式:
?
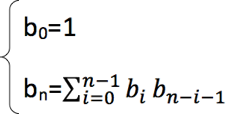
?
通過對公式一步步的數學推算,最后得出,含有 n 個結點的不相似的二叉樹的數量為:
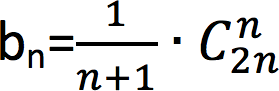
【方法二】
從遍歷二叉樹的角度進行分析,對于任意一棵二叉樹來說,它的前序序列和中序序列以及后序序列都是唯一的。其實是這句話還可以倒過來說,只要確定了一棵二叉樹的三種遍歷序列中的兩種,那么這棵二叉樹也可以唯一確定。
例如,給定了一個二叉樹的前序序列和中序序列分別為:
前序序列:A B C D E F G
中序序列:C B E D A F G
可以唯一得到的二叉樹如圖 2(4):
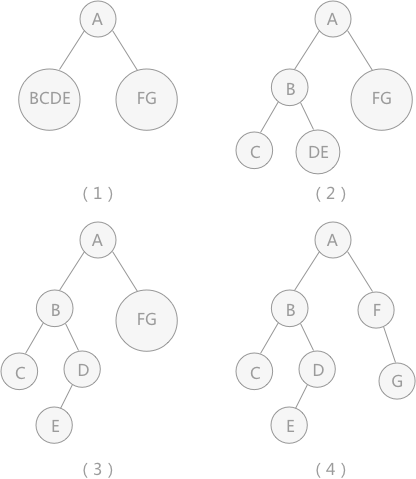
圖 2 構造二叉樹的過程示意圖
分析:通過前序序列得知,結點A為二叉樹的根結點,結合中序序列,在結點 A 左側的肯定為其左孩子中的所有結點,右邊為右孩子的所有結點,如圖 2(1)所示。
再分析 A 結點的左孩子,在前序序列看到,結點 A 后緊跟的是結點 B,由此斷定結點 A 的左孩子是 B,再看中序序列,結點 B 左側只有一個結點 C ,為 B 的左孩子,結點 B 右側的結點E 和 D 為右孩子,如圖 2(2)。
再分析結點 B 的右孩子,前序序列看到,結點 D 在 E 的前邊,所有 D 為 B 的右孩子。在中序序列中,結點 E 在 D 前邊,說明 E 是 D 的左孩子,如圖 2(3)。
最后分析結點 A 的右孩子,由前序序列看到, F 在 G 前邊,說明F為根結點。在中序序列中也是如此,說明,G 是 F 的右孩子。如圖 2(4)所示。
如果要唯一確定一棵二叉樹,必須知道至少兩種遍歷序列。如果只確定一種序列,無法準確判定二叉樹的具體構造。
?
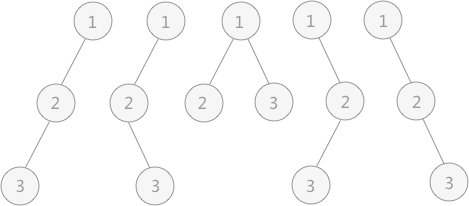
圖 3 前序序列(1,2,3)的二叉樹
如圖 3 所示為前序序列(1,2,3)構建的不同形態的二叉樹,他們的中序序列各不相同。所以不同形態二叉樹的數目恰好就是前序序列一定的情況下,所能得到的不同的中序序列的個數。
中序序列是對二叉樹進行中序遍歷獲得的,遍歷的過程實質上就是結點數據進棧出棧的過程。所以,中序序列的個數就是數列(1,2,3)按1-2-3的順序進棧,各元素選擇在不同的時間點出棧,所獲的的不同的出棧順序即為中序序列,而中序序列的數目,也就是不同形態的二叉樹的個數。
?
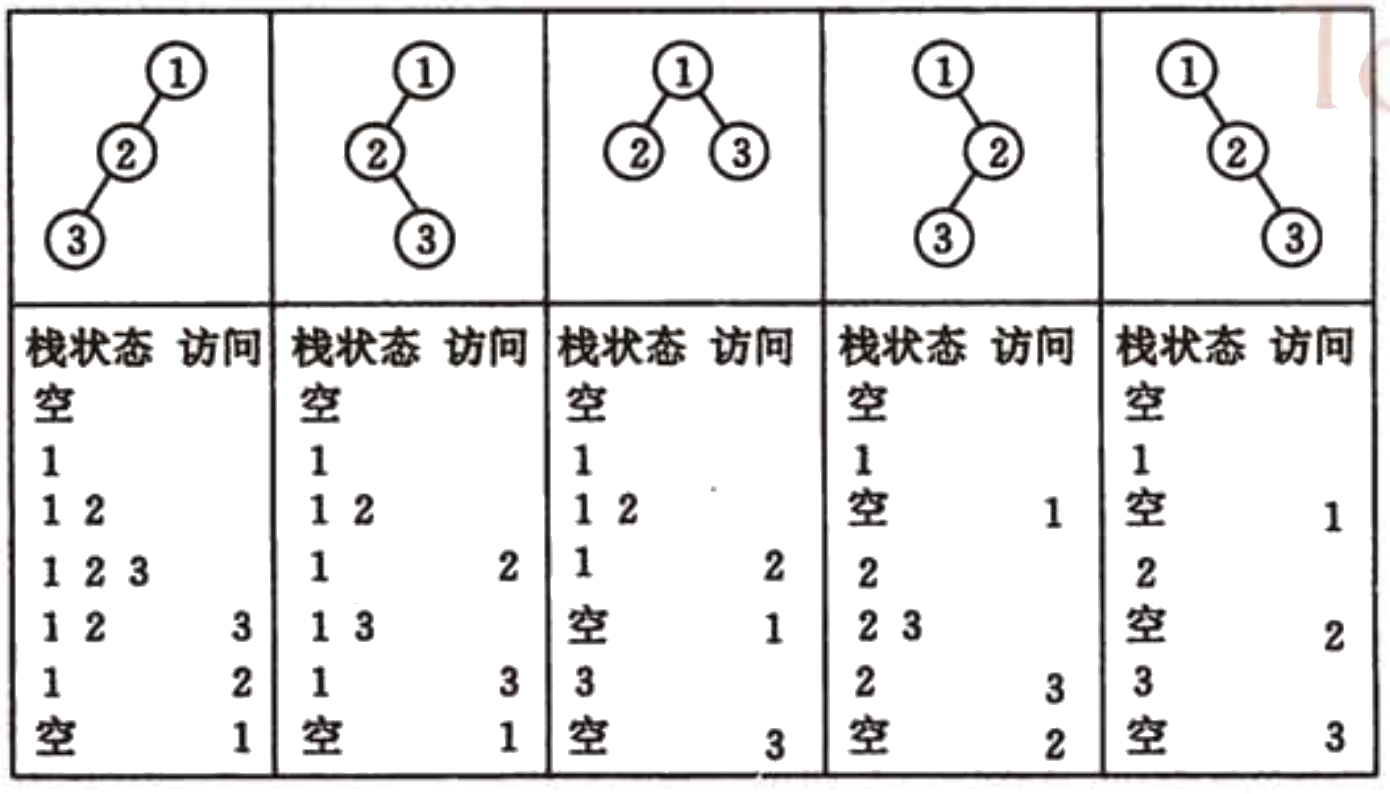
圖 4 中序遍歷時進棧和出棧的過程
根據數列中數據的個數 n,所得到的排列順序的數目為:
?
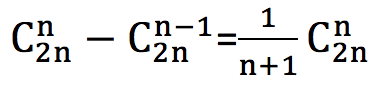
?
通過以上兩種方式,都可以知道 n 個結點能構建的不同形態的二叉樹的數量,再結合?tn=bn-1,就可以計算出 n 個結點能構建的不同形態的樹的個數。

)
)

)














)