拉丁方設計（Latin square design）：實驗研究中涉及一個處理因素和兩個控制因素，每個因素的類別數或水平數相等，此時可采用拉丁方設計，將兩個控制因素分別安排在拉丁方設計的行和列上。該設計類型仍為單因素方差分析。拉丁方設計是隨機區組設計的一種推廣或延續，可多安排一個已知的對實驗結果有影響的非處理因素。在對拉丁方設計試驗結果進行統計分析時，由于能將橫行、列行二個單位組間的變異從試驗誤差中分離出來，抵消由于實驗處理的先后順序的影響而產生的順序誤差。拉丁方設計資料的表格排序可參考相關文獻或書籍。

拉丁方設計資料的一般形式

?

案例分析
某研究者為了比較甲、乙、丙、丁、戊、己6種藥物給家兔注射后產生的皮膚皰疹大小（mm2），采用拉丁方設計，選用6只家兔并在每只家兔的6個不同部位進行注射。實驗結果整理如下。

?

（拉丁方字母 A~F 代表六種藥物，為處理因素）

數據視圖

?

案例剖析

研究目的：為了比較甲、乙、丙、丁、戊、己6種藥物給家兔注射后產生的皮膚皰疹大小有無差別。
變量類型：一個處理因素，即6種藥物，為分類變量；兩個控制因素：6只家兔和6個不同注射部位，為分類變量；反應變量：皮膚皰疹大小。
統計分析方法：從專業上判斷因素間相互作用的影響可忽略，故采用拉丁方設計資料的方差分析。適用條件：樣本數據滿足獨立性、正態性、方差性；否則采用數據變換或者非參數檢驗。
操作步驟

由專業知識可知，數據滿足獨立性；通過S-W檢驗或Q-Q圖可判斷數據服從正態分布；由殘差圖或Levene's 檢驗可知，數據滿足方差齊性檢驗。

（Ⅰ）

General?Linear Model???Univariate

?

（Ⅱ）

選入相應的變量

?

（Ⅲ）單擊?Model

各因子均為主效應（main effect），不需考慮其他效應

?

（Ⅳ）單擊?Option

比較處理組（藥物）之間的差異；可根據具體需要勾選相應的統計量；

?

結果分析

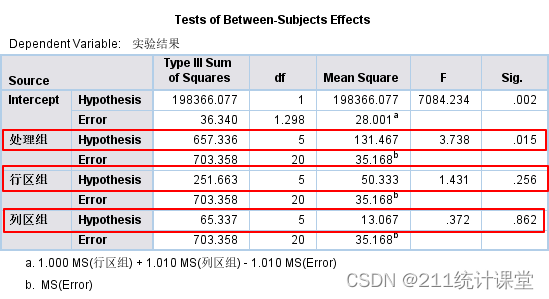
（●）主效應檢驗

處理組（藥物，F=3.738，p=0.015），拒絕H0，即6種藥物注射后家兔產生皮膚皰疹大小的總體均數不全相等。行區組（家兔編號，F=1.431，p=0.256）和列區組（注射部位，F=0.372，p=0.862）與皮膚皰疹大小無統計學差異。

?

（●●）

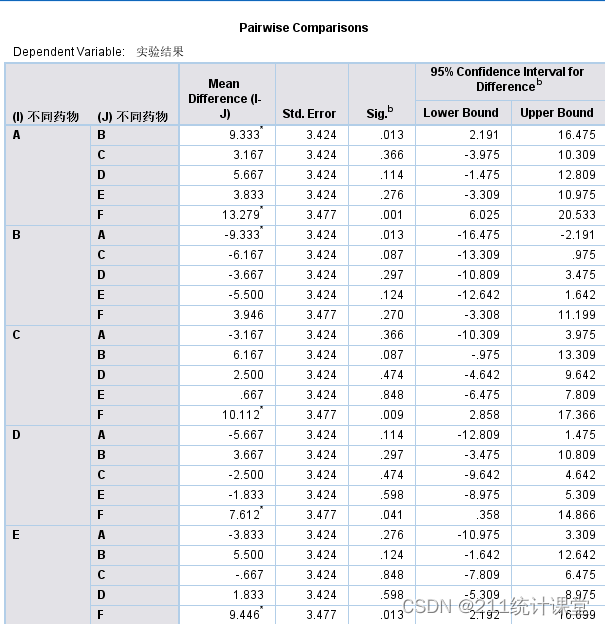
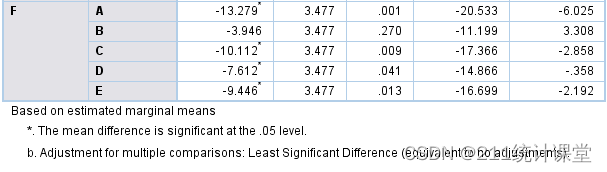
6種不同藥物的兩兩比較

?

SAS

<SAS代碼可左右滑動查看>

?

?

?

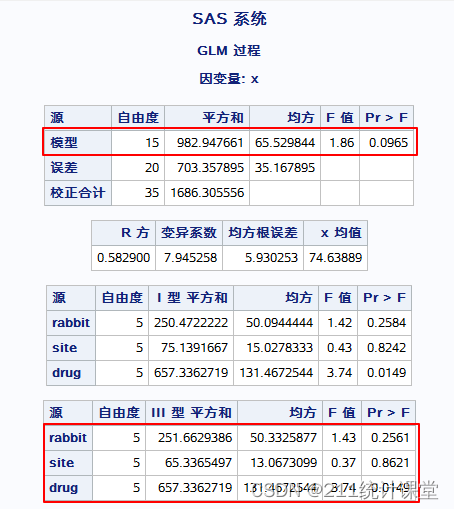
SAS運行結果

釋結果與SPSS一致，這里不作重復贅述。

?