導讀:浮點數運算是一個非常有技術含量的話題,不太容易掌握。許多程序員都不清楚使用==操作符比較float/double類型的話到底出現什么問題。 許多人使用float/double進行貨幣計算時經常會犯錯。這篇文章是這一系列中的精華,所有的軟件開發人員都應該讀一下。
隨著你經驗的增長,你肯定 想去深入了解一些常見的東西的細節,浮點數運算就是其中之一。
1. 什么是浮點數?
在計算機系統的發展過程中,曾經提出過多種方法表達實數。
【1】典型的比如相對于浮點數的定點數(Fixed Point Number)。在這種表達方式中,小數點固定的位于實數所有數字中間的某個位置。貨幣的表達就可以使用這種方式,比如 99.00 或者 00.99 可以用于表達具有四位精度(Precision),小數點后有兩位的貨幣值。由于小數點位置固定,所以可以直接用四位數值來表達相應的數值。SQL 中的 NUMBER 數據類型就是利用定點數來定義的。
【2】還有一種提議的表達方式為有理數表達方式,即用兩個整數的比值來表達實數。
定點數表達法的缺點在于其形式過于僵硬,固定的小數點位置決定了固定位數的整數部分和小數部分,不利于同時表達特別大的數或者特別小的數。最終,絕大多數現代的計算機系統采納了所謂的浮點數表達方式。
【3】浮點數表達方式, 這種表達方式利用科學計數法來表達實數,即用一個尾數(Mantissa ),一個基數(Base),一個指數(Exponent)以及一個表示正負的符號來表達實數。比如 123.45 用十進制科學計數法可以表達為 1.2345 × 102 ,其中 1.2345 為尾數,10 為基數,2 為指數。浮點數利用指數達到了浮動小數點的效果,從而可以靈活地表達更大范圍的實數。提示: 尾數有時也稱為有效數字(Significand)。尾數實際上是有效數字的非正式說法。
同樣的數值可以有多種浮點數表達方式,比如上面例子中的 123.45 可以表達為 12.345 × 101,0.12345 × 103 或者 1.2345 × 102。因為這種多樣性,有必要對其加以規范化以達到統一表達的目標。規范的(Normalized)浮點數表達方式具有如下形式:
d.dd...d × βe?, (0 ≤ di?< β)
其中?d.dd...d 即尾數,β 為基數,e 為指數。尾數中數字的個數稱為精度,在本文中用 p(presion) 來表示。每個數字 d 介于 0 和基數β之間,包括 0。小數點左側的數字不為 0。
(1) 基于規范表達的浮點數對應的具體值可由下面的表達式計算而得:(p是精度個數)
±(d0 + d1β-1 + ... + dp-1β-(p-1))βe , (0 ≤ di < β)
對于十進制的浮點數,即基數 β 等于 10 的浮點數而言,上面的表達式非常容易理解,也很直白。計算機內部的數值表達是基于二進制的。從上面的表達式,我們可以知道,二進制數同樣可以有小數點,也 同樣具有類似于十進制的表達方式。只是此時 β 等于 2,而每個數字 d 只能在 0 和 1 之間取值。
(2) 比如二進制數 1001.101 相當于:精度為7
1 × 2?3?+ 0 × 22?+ 0 × 21?+ 1 × 20?+ 1 × 2-1?+ 0 × 2-2?+ 1 × 2-3,對應于十進制的 9.625。
其規范浮點數表達為 1.001101 × 23。
(3) IEEE (美國電氣和電子工程師學會)浮點數
計算機中是用有限的連續字節保存浮點數的。
IEEE定義了多種浮點格式,但最常見的是三種類型:單精度、雙精度、擴展雙精度,分別適用于不同的計算要求。一般而言,單精度適合一般計算,雙精度適合科學計算,擴展雙精度適合高精度計算。一個遵循IEEE 754標準的系統必須支持單精度類型(強制類型)、最好也支持雙精度類型(推薦類型),至于擴展雙精度類型可以隨意。單精度(Single Precision)浮點數是32位(即4字節)的,雙精度(Double Precision)浮點數是64位(即8字節)的。
保存這些浮點數當然必須有特定的格式,Java 平臺上的浮點數類型 float 和 double 采納了 IEEE 754 標準中所定義的單精度 32 位浮點數和雙精度 64 位浮點數的格式。注意:?Java 平臺還支持該標準定義的兩種擴展格式,即 float-extended-exponent 和 double-extended-exponent 擴展格式。這里將不作介紹,有興趣的讀者可以參考相應的參考資料。
在 IEEE 標準中,浮點數是將特定長度的連續字節的所有二進制位分割為特定寬度的符號域,指數域和尾數域三個域,其中保存的值分別用于表示給定二進制浮點數中的符號,指數和尾數。這樣,通過尾數和可以調節的指數(所以稱為"浮點")就可以表達給定的數值了。
具體的格式參見下面的表格:

需要特別注意的是,擴展雙精度類型沒有隱含位,因此它的有效位數與尾數位數一致,而單精度類型和雙精度類型均有一個隱含位,因此它的有效位數比位數位數多一個。
?
IEEE754標準規定一個實數V可以用: V=(-1)s×M×2^E的形式表示,說明如下:
(1)符號s(sign)決定實數是正數(s=0)還是負數(s=1),對數值0的符號位特殊處理。
(2)有效數字M是二進制小數,M的取值范圍在1≤M<2或0≤M<1。
(3)指數E(exponent)是2的冪,它的作用是對浮點數加權。
? 為了強制定義一些特殊值,IEEE標準通過指數將表示空間劃分成了三大塊:
【1】最小值指數(所有位全置0)用于定義0和弱規范數
【2】最大指數(所有位全值1)用于定義±∞和NaN(Not a Number)
【3】其他指數用于表示常規的數。
這樣一來,最大(指絕對值)常規數的指數不是全1的,最小常規數的指數也不是0,而是1。

?
S:符號位, Exponent:指數域 Fraction:尾數域
注意:尾數有時也稱為有效數字(Significand),
一般如1.001001*2EValue,即一個尾數(Mantissa ),一個基數(底數Base),一個指數Evalue表示
即: M * BE?=?尾數 * 底數指數
通常情況,IEEE標準寫法,尾數的1,省略,Fraction= 0.001001,因為標準寫法,前面的1總是省略?Fraction = 尾數 - 1?;(IEEE規定小數點左側的 1 是隱藏的)
如果指數值:加上相應的浮點數偏執后的值:即?Exponent = EValue + Bias。
所以上述的值: X = (-1)S? X ( 1 + Fraction)?(Exponent - Bias), 也就不足為奇了
?
在上面的圖例中:
① 第一個域:為符號域。其中?0 表示數值為正數,而 1 則表示負數。
② 第二個域為指數域,對應于我們之前介紹的二進制科學計數法中的指數部分。
指數閾:通常使用移碼表示:
(移碼和補碼只有符號位相反,其余都一樣。對于正數而言,原碼、反碼和補碼都一樣;對于負數而言,補碼就是其絕對值的原碼全部取反,然后加1(不包括符號位))。
其中單精度數為 8 位,雙精度數為 11 位。以單精度數為例,8 位的指數為可以表達 0 到 255 之間的 255 個指數值。
但是,指數可以為正數,也可以為負數。為了處理負指數的情況,實際的指數值按要求需要加上一個偏差(Bias)值作為保存在指數域中的值,單精度數的偏差值為 127(0-111 1111)(8位),而雙精度數的偏差值為 1023(0-1 1111 1111)(10位)。比如,單精度的實際指數值 0?在指數域中將保存為 127;而保存在指數域中的 64 則表示實際的指數值 -63。偏差的引入使得對于單精度數,實際可以表達的指數值的范圍就變成 -127 到 128 之間(包含兩端)[-127, 128]。
我們不久還將看到:
實際的指數值 -127(保存為 全 0),即: 首先-127原碼1-111 1111,的補碼1-000 0001,然后加上單精度偏執: 0-111 111 ,即結果:0-000 0000,全0. 所以0-000 0000 指數位表示:-127,即e-127
以及 +128(保存為全 1), 即:首先+128原碼‘1’-000 0000,的補碼, ‘1’-000 0000,然后加上單精度偏執:0-111 111 ,, 即結果:‘1’-111 1111,全1。? 即全1 指數位表示:+128,即e+128
這些特殊值,保留用作特殊值的處理。這樣,實際可以表達的有效指數范圍就在 -127 和 127 之間。在本文中,最小指數和最大指數分別用 emin 和 emax 來表達。
?
計算機中的符號數有三種表示方法,即原碼、反碼和補碼。
如補碼的求取:
① 正數(符號位為0的數)補碼與原碼相同.
② 負數(符號位為1的數)變為補碼時符號位不變,其余各項取反,最后在末尾+1;即求負數的反碼不包括符號位。
例如:正數 原碼01100110,補碼為:01100110
負數 原碼11100110,先變反碼:10011001,再加1變為補碼:10011010
計算機中的符號數有三種表示方法,即原碼、反碼和補碼。三種表示方法均有符號位和數值位兩部分,符號位都是用0表示“正”,用1表示“負”,而數值位,三種表示方法各不相同。
在計算機系統中,數值一律用補碼來表示和存儲。原因在于:①使用補碼,可以將符號位和數值域統一處理;②同時,加法和減法也可以統一處理。此外,③補碼與原碼相互轉換,其運算過程是相同的,不需要額外的硬件電路。
特性
① 一個負整數(或原碼)與其補數(或補碼)相加,和為模。eg:原碼11100110, 補碼:10011010 和:
② 對一個整數的補碼再求補碼,等于該整數自身。
③ 補碼的正零與負零表示方法相同。即 0-0000000, 1-0000000取反加1, 0-0000000
?
③ 圖例中的第三個域為尾數域,其中單精度數為 23 位長,雙精度數為 52 位長。除了我們將要講到的某些特殊值外,IEEE 標準要求浮點數必須是規范的。這意味著尾數的小數點左側必須為 1,因此我們在保存尾數的時候,可以省略小數點前面這個 1,從而騰出一個二進制位來保存更多的尾數。這樣我們實際上用 23 位長的尾數域表達了 24 位的尾數。比如對于單精度數而言,二進制的 1001.101(對應于十進制的 9.625)可以表達為 1.001101 × 23,所以實際保存在尾數域中的值為 00110100000000000000000,即去掉小數點左側的 1,并用 0 在右側補齊。
? 根據IEEE(美國電氣和電子工程師學會)754標準要求,無法精確保存的值必須向最接近的可保存的值進行舍入。這有點像我們熟悉的十進制的四舍五入,即不足一半則舍,一半以上(包括一半)則進。不過對于二進制浮 點數而言,還多一條規矩,就是當需要舍入的值剛好是一半時,不是簡單地進,而是在前后兩個等距接近的可保存的值中,取其中最后一位有效數字為零者。從上面 的示例中可以看出,奇數都被舍入為偶數,且有舍有進。我們可以將這種舍入誤差理解為"半位"的誤差。所以,為了避免 7.22 對很多人造成的困惑,有些文章經常以 7.5 位來說明單精度浮點數的精度問題。
據以上分析,IEEE 754標準中定義浮點數的表示范圍為:
單精度浮點數 二進制:± (2-2^-23) × 2127 對應十進制: ~ ± 10^38.53
雙精度浮點數 ? 二進制:± (2-2^-52) × 21023
浮點數的表示有一定的范圍,超出范圍時會產生溢出(Flow),一般稱大于絕對值最大的數據為上溢(Overflow),小于絕對值最小的數據為下溢(Underflow)。
?
2.?浮點數的表示約定
單精度浮點數和雙精度浮點數都是用IEEE 754標準定義的,其中有一些特殊約定,例如:
(1) 當P=0,M=0時,表示0。
(2) 當P=255,M=0時,表示無窮大,用符號位來確定是正無窮大還是負無窮大。
(3) 當P=255,M≠0時,表示NaN(Not a Number,不是一個數)。
?
3.?特殊值
通過前面的介紹,你應該已經了解的浮點數的基本知識,這些知識對于一個不接觸浮點數應用的人應該足夠了。不過,如果你興趣正濃,或者面對著一個棘手的浮點數應用,可以通過本節了解到關于浮點數的一些值得注意的特殊之處。
我們已經知道,單精度浮點數指數域實際可以表達的指數值的范圍為 -127 到 128 之間(包含兩端)。其中,值 -127(保存為全0)以及 +128(保存為全1)保留用作特殊值的處理。本節將詳細 IEEE 標準中所定義的這些特殊值。
浮點數中的特殊值主要用于特殊情況或者錯誤的處理。比如在程序對一個負數進行開平方時,一個特殊的返回值將用于標記這種錯誤,該值為 NaN(Not a Number)。沒有這樣的特殊值,對于此類錯誤只能粗暴地終止計算。除了 NaN 之外,IEEE 標準還定義了 ±0,±∞ 以及非規范化數(Denormalized Number)。
對于單精度浮點數,所有這些特殊值都由保留的特殊指數值 -127 和 128 來編碼。如果我們分別用?emin?和?emax?來表達其它常規指數值范圍的邊界,即 -126 和 127,則保留的特殊指數值可以分別表達為?emin?- 1 和?emax?+ 1; 。基于這個表達方式,IEEE 標準的特殊值如下所示:

其中?f?表示尾數中的小數點右側的(Fraction)部分,即標準記法中的有效部分-1。
第一行即我們之前介紹的普通的規范化浮點數。隨后我們將分別對余下的特殊值加以介紹。
第2,3,4,5行,是特殊值。
(1)NaN
NaN 用于處理計算中出現的錯誤情況,比如 0.0 除以 0.0 或者求負數的平方根。
由上面的表中可以看出,對于單精度浮點數,NaN 表示為指數為?emax?+ 1 =?128(指數域全為 1),且尾數域不等于零的浮點數。IEEE 標準沒有要求具體的尾數域,所以?NaN 實際上不是一個,而是一族。
不同的實現可以自由選擇尾數域的值來表達 NaN,比如 Java 中的常量 Float.NaN 的浮點數可能表達為 0-11111111-10000000000000000000000,其中尾數域的第一位為 1,其余均為 0(不計隱藏的一位),但這取決系統的硬件架構。Java 中甚至允許程序員自己構造具有特定位模式的 NaN 值(通過 Float.intBitsToFloat() 方法)。比如,程序員可以利用這種定制的 NaN 值中的特定位模式來表達某些診斷信息。定制的 NaN 值,可以通過 Float.isNaN() 方法判定其為 NaN,但是它和 Float.NaN 常量卻不相等。
實際上,所有的 NaN 值都是無序的。數值比較操作符 <,<=,> 和 >= 在任一操作數為 NaN 時均返回 false。等于操作符 == 在任一操作數為 NaN 時均返回 false,即使是兩個具有相同位模式的 NaN 也一樣。而操作符 != 則當任一操作數為 NaN 時返回 true。
這個規則的一個有趣的結果是 x!=x 當 x 為 NaN 時竟然為真。
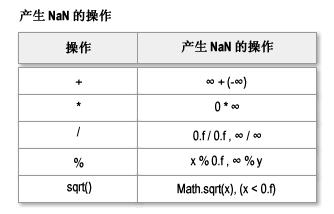
此外,任何有 NaN 作為操作數的操作也將產生 NaN。用特殊的 NaN 來表達上述運算錯誤的意義在于避免了因這些錯誤而導致運算的不必要的終止。比如,如果一個被循環調用的浮點運算方法,可能由于輸入的參數問題而導致發生這些錯誤,NaN 使得 即使某次循環發生了這樣的錯誤,也可以簡單地繼續執行循環以進行那些沒有錯誤的運算。你可能想到,既然 Java 有異常處理機制,也許可以通過捕獲并忽略異常達到相同的效果。但是,要知道,IEEE 標準不是僅僅為 Java 而制定的,各種語言處理異常的機制不盡相同,這將使得代碼的遷移變得更加困難。何況,不是所有語言都有類似的異常或者信號(Signal)處理機制。
(2)無窮
和 NaN 一樣,特殊值無窮(Infinity)的指數部分同樣為 emax + 1 = 128,不過無窮的尾數域必須為零。無窮用于表達計算中產生的上溢(Overflow)問題。比如兩個極大的數相乘時,盡管兩個操作數本身可以用保存為浮點數,但其結果可能大到無法保存為浮點數,而必須進行舍入。根據 IEEE 標準,此時不是將結果舍入為可以保存的最大的浮點數(因為這個數可能離實際的結果相差太遠而毫無意義),而是將其舍入為無窮。對于負數結果也是如此,只不過此時舍入為負無窮,也就是說符號域為 1 的無窮。有了 NaN 的經驗我們不難理解,特殊值無窮使得計算中發生的上溢錯誤不必以終止運算為結果。
無窮和除 NaN 以外的其它浮點數一樣是有序的,從小到大依次為負無窮,負的有窮非零值,正負零(隨后介紹),正的有窮非零值以及正無窮。除 NaN 以外的任何非零值除以零,結果都將是無窮,而符號則由作為除數的零的符號決定。
回顧我們對 NaN 的介紹,當零除以零時得到的結果不是無窮而是 NaN 。原因不難理解,當除數和被除數都逼近于零時,其商可能為任何值,所以 IEEE 標準決定此時用 NaN 作為商比較合適。
(3)有符號的零
因為 IEEE 標準的浮點數格式中,小數點左側的 1 是隱藏的,而零顯然需要尾數必須是零。所以,零也就無法直接用這種格式表達而只能特殊處理。實際上,零保存為尾數域為全為 0,指數域為 emin - 1 = -127,也就是說指數域也全為 0。考慮到符號域的作用,所以存在著兩個零,即 +0 和 -0。不同于正負無窮之間是有序的,IEEE 標準規定正負零是相等的。
零有正負之分,的確非常容易讓人困惑。這一點是基于數值分析的多種考慮,經利弊權衡后形成的結果。有符號的零可以避免運算中,特別是涉及無窮的運算中,符號信息的丟失。舉例而言,如果零無符號,則等式 1/(1/x) = x 當x = ±∞ 時不再成立。原因是如果零無符號,1 和正負無窮的比值為同一個零,然后 1 與 0 的比值為正無窮,符號沒有了。解決這個問題,除非無窮也沒有符號。但是無窮的符號表達了上溢發生在數軸的哪一側,這個信息顯然是不能不要的。零有符號也造成了其它問題,比如當 x=y 時,等式1/x = 1/y 在 x 和 y 分別為 +0 和 -0 時,兩端分別為正無窮和負無窮而不再成立。當然,解決這個問題的另一個思路是和無窮一樣,規定零也是有序的。但是,如果零是有序的,則即使 if (x==0) 這樣簡單的判斷也由于 x 可能是 ±0 而變得不確定了。兩害取其輕者,零還是無序的好。
(4)非規范化數
我們來考察浮點數的一個特殊情況。選擇兩個絕對值極小的浮點數,以單精度的二進制浮點數為例,比如 1.001 × 2-125 和 1.0001 × 2-125 這兩個數(分別對應于十進制的 2.6448623 × 10-38 和 2.4979255 × 10-38)。顯然,他們都是普通的浮點數(指數為 -125,大于允許的最小值 -126;尾數更沒問題),按照 IEEE 754 可以分別保存為 00000001000100000000000000000000(0x1100000)和 00000001000010000000000000000000(0x1080000)。
現在我們看看這兩個浮點數的差值。不難得出,該差值為 0.0001 × 2-125,表達為規范浮點數則為 1.0 × 2-129。問題在于其指數大于允許的最小指數值,所以無法保存為規范浮點數。最終,只能近似為零(Flush to Zero)。這中特殊情況意味著下面本來十分可靠的代碼也可能出現問題:
if (x != y) {z = 1 / (x -y);} 正如我們精心選擇的兩個浮點數展現的問題一樣,即使?x 不等于 y,x 和 y 的差值仍然可能絕對值過小,而近似為零,導致除以 0 的情況發生。
為了解決此類問題,IEEE 標準中引入了非規范(Denormalized)浮點數。規定當浮點數的指數為允許的最小指數值,即 emin 時,尾數不必是規范化的。比如上面例子中的差值可以表達為非規范的浮點數 0.001 × 2-126,其中指數 -126 等于 emin。注意,這里規定的是"不必",這也就意味著"可以"。當浮點數實際的指數為 emin,且指數域也為 emin 時,該浮點數仍是規范的,也就是說,保存時隱含著一個隱藏的尾數位。為了保存非規范浮點數,IEEE 標準采用了類似處理特殊值零時所采用的辦法,即用特殊的指數域值 emin - 1?加以標記,當然,此時的尾數域不能為零。這樣,例子中的差值可以保存為 00000000000100000000000000000000(0x100000),沒有隱含的尾數位。
有了非規范浮點數,去掉了隱含的尾數位的制約,可以保存絕對值更小的浮點數。而且,也由于不再受到隱含尾數域的制約,上述關于極小差值的問題也不存在了,因為所有可以保存的浮點數之間的差值同樣可以保存。
4.?范圍和精度
很多小數根本無法在二進制計算機中精確表示(比如最簡單的 0.1)由于浮點數尾數域的位數是有限的,為此,浮點數的處理辦法是持續該過程直到由此得到的尾數足以填滿尾數域,之后對多余的位進行舍入。
換句話說,除了我們之前講到的精度問題之外,十進制到二進制的變換也并不能保證總是精確的,而只能是近似值。
事實上,只有很少一部分十進制小數具有精確的二進制浮點數表達。再加上浮點數運算過程中的誤差累積,結果是很多我們看來非常簡單的十進制運算在計算機上卻往往出人意料。這就是最常見的浮點運算的"不準確"問題。
參見下面的 Java 示例:
System.out.print("34.6-34.0=" + (34.6f-34.0f)); 這段代碼的輸出結果如下:
34.6-34.0=0.5999985
產生這個誤差的原因是?34.6 無法精確的表達為相應的浮點數,而只能保存為經過舍入的近似值。這個近似值與 34.0 之間的運算自然無法產生精確的結果。
存儲格式的范圍和精度如下表所示:

5. 舍入
值得注意的是,對于單精度數,由于我們只有?24 位的尾數(其中一位隱藏),所以可以表達的最大指數為 224?- 1 = 16,777,215。
特別的,16,777,216 是偶數,所以我們可以通過將它除以 2 并相應地調整指數來保存這個數,這樣 16,777,216 同樣可以被精確的保存。相反,數值 16,777,217 則無法被精確的保存。由此,我們可以看到單精度的浮點數可以表達的十進制數值中,真正有效的數字不高于 8 位。
事實上,對相對誤差的數值分析結果顯示有效的精度大約為 7.22 位。
實例如下所示:
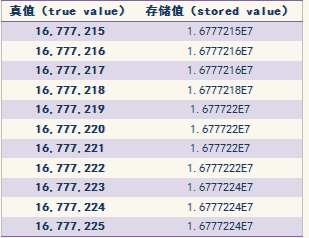
根 據標準要求,無法精確保存的值必須向最接近的可保存的值進行舍入。這有點像我們熟悉的十進制的四舍五入,即不足一半則舍,一半以上(包括一半)則進。不過 對于二進制浮點數而言,還多一條規矩,就是當需要舍入的值剛好是一半時,不是簡單地進,而是在前后兩個等距接近的可保存的值中,取其中最后一位有效數字為 零者。從上面的示例中可以看出,奇數都被舍入為偶數,且有舍有進。我們可以將這種舍入誤差理解為"半位"的誤差。所以,為了避免 7.22 對很多人造成的困惑,有些文章經常以 7.5 位來說明單精度浮點數的精度問題。
提示:?這里采用的浮點數舍入規則有時被稱為舍入到偶數(Round to Even)。相比簡單地逢一半則進的舍入規則,舍入到偶數有助于從某些角度減小計算中產生的舍入誤差累積問題。因此為 IEEE 標準所采用。

)
)
![#loj 3058 [HNOI2019] 白兔之舞](http://pic.xiahunao.cn/#loj 3058 [HNOI2019] 白兔之舞)


基礎工程代碼閱讀)

)
)
)

)






)