題目

給定兩個整數數組?preorder?和?inorder?，其中?preorder?是二叉樹的先序遍歷，?inorder?是同一棵樹的中序遍歷，請構造二叉樹并返回其根節點。

示例 1:

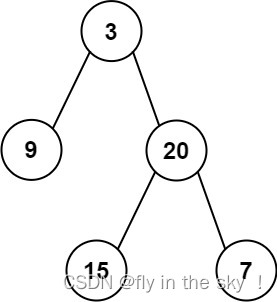
輸入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
輸出: [3,9,20,null,null,15,7]

示例 2:

輸入: preorder = [-1], inorder = [-1]
輸出: [-1]

提示:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder?和?inorder?均?無重復?元素
• inorder?均出現在?preorder
• preorder?保證?為二叉樹的前序遍歷序列
• inorder?保證?為二叉樹的中序遍歷序列

前置知識:?

preorder?:前序遍歷(Preorder Traversal 亦稱先序遍歷)——訪問根結點--->根的左子樹--->根的右子樹。

inorder:中序遍歷(Inorder Traversal)——根的左子樹--->根節點--->根的右子樹

前序遍歷所得的第一個節點就是根節點,所以可以用來確定的是root根節點在中序遍歷的位置,

再根據中序遍歷,root根節點的左邊是這棵二叉樹的左樹,root根節點的右邊是這課二叉樹的右樹來構建這課二叉樹

以示例1為例談談對題目的理解

示例1輸入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]

preorder = [??3,? 9,? 20,? 15,? 7? ]? ?3就為這棵二叉樹的root根節點

inorder = [? 9,??3,? 15,? 20,? 7? ]? 9為root的左樹,并且只有一個節點,所以9為root的左節點

15,20,7這三個節點為root的右樹,再根據中序遍歷根的左子樹--->根節點--->根的右子樹可得

root的右節點為20這個節點,20節點的左節點為15這個節點,右節點為7這個節點

畫圖演示上述文字說明

---

解題思路:

根據題目所給的前序遍歷的節點順序在中序遍歷中進行遞歸來構建二叉樹

1.根據前序遍歷找到中序遍歷根節點iRoot的位置,創建根節點,再確定iBegin,iEnd的位置,i++;

2.對iBegin和iEnd的位置進行判斷,當iBegin>iEnd時,返回null,遞歸開始回退;

2.在中序遍歷當中，根據iRoot ,iBegin,iEnd的位置,并進行左樹和右樹的構建;

對上述三步進行遞歸,遞歸完了之后,二叉樹構建完成,返回根節點root

注:對前序遍歷所得節點的利用才是本題代碼的靈魂所在

圖示:

---

解題代碼

class Solution {public int i = 0;public TreeNode buildTree(int[] preorder, int[] inorder) {return create_a_binary_tree(preorder, inorder, 0, inorder.length - 1);}public TreeNode create_a_binary_tree(int[] preorder, int[] inorder, int inBegin, int inEnd) {if (inBegin > inEnd) {return null;//給定的數組int[] preorder, int[] inorder,遍歷完了,沒有子樹了,該節點為空節點,返回null,遞歸開始回退}//先根據先序遍歷創建根節點TreeNode root = new TreeNode(preorder[i]);//找到當前根節點,在中序遍歷的位置int rootIndex = findIndex(inorder, inBegin, inEnd, preorder[i]);i++;//遞歸構建左樹root.left = create_a_binary_tree(preorder, inorder, inBegin, rootIndex - 1);//遞歸構建右樹root.right = create_a_binary_tree(preorder, inorder, rootIndex + 1, inEnd);//前序遍歷完成,返回根節點return root;}private int findIndex(int[] inorder, int inBegin, int inEnd, int key) {for (int j = inBegin; j <= inEnd; j++) {if (inorder[j] == key) {return j;}}return -1;}
}

運行結果

題目鏈接

https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/submissions/

舉一翻三,再來一道

根據一棵樹的中序遍歷與后序遍歷構造二叉樹

給定兩個整數數組?inorder?和?postorder?，其中?inorder?是二叉樹的中序歷，?postorder?是同一棵樹的后序遍歷，請你構造并返回這顆?二叉樹?。

示例 1:

輸入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
輸出：[3,9,20,null,null,15,7]

示例 2:

輸入：inorder = [-1], postorder = [-1]
輸出：[-1]

后序遍歷(Postorder Traversal)——根的左子樹--->根的右子樹--->根節點。
創建根節點后,先創建右數,再創建左樹

根據示例1進行講解,下圖是代碼遞歸過程

隨著代碼的遞歸,二叉樹隨之構建的過程?

?解題代碼

public class Solution {public int i = 0;public TreeNode buildTree(int[] inorder, int[] postorder) {i = postorder.length - 1;return create_a_binary_tree(postorder, inorder, 0, inorder.length - 1);}public TreeNode create_a_binary_tree(int[] postorder, int[] inorder, int inBegin, int inEnd) {if (inBegin > inEnd) {return null;//給定的數組int[] postorder, int[] inorder,遍歷完了,沒有子樹了,該節點為空節點,返回null,遞歸開始回退}//先根據先序遍歷創建根節點TreeNode root = new TreeNode(postorder[i]);//找到當前根節點,在中序遍歷的位置int rootIndex = findIndex(inorder, inBegin, inEnd, postorder[i]);i--;//遞歸先構建右樹root.right = create_a_binary_tree(postorder, inorder, rootIndex + 1, inEnd);//遞歸后構建左樹root.left = create_a_binary_tree(postorder, inorder, inBegin, rootIndex - 1);//前序遍歷完成,返回根節點return root;}private int findIndex(int[] inorder, int inBegin, int inEnd, int key) {for (int j = inBegin; j <= inEnd; j++) {if (inorder[j] == key) {return j;}}return -1;}
}

運行結果

題目鏈接:

https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/submissions/

完結撒花??ヽ(°▽°)ノ??