目錄

哈夫曼樹（赫夫曼樹、最優樹）詳解

哈夫曼樹相關的幾個名詞

什么是哈夫曼樹

構建哈夫曼樹的過程

哈弗曼樹中結點結構

構建哈弗曼樹的算法實現

---

哈夫曼樹（赫夫曼樹、最優樹）詳解

哈夫曼樹相關的幾個名詞

路徑：在一棵樹中，一個結點到另一個結點之間的通路，稱為路徑。圖 1 中，從根結點到結點 a 之間的通路就是一條路徑。

路徑長度：在一條路徑中，每經過一個結點，路徑長度都要加 1 。例如在一棵樹中，規定根結點所在層數為1層，那么從根結點到第 i 層結點的路徑長度為 i - 1 。圖 1 中從根結點到結點 c 的路徑長度為 3。

結點的權：給每一個結點賦予一個新的數值，被稱為這個結點的權。例如，圖 1 中結點 a 的權為 7，結點 b 的權為 5。

結點的帶權路徑長度：指的是從根結點到該結點之間的路徑長度與該結點的權的乘積。例如，圖 1 中結點 b 的帶權路徑長度為 2 * 5 = 10 。

樹的帶權路徑長度為樹中所有葉子結點的帶權路徑長度之和。通常記作?“WPL”?。例如圖 1 中所示的這顆樹的帶權路徑長度為：

WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3

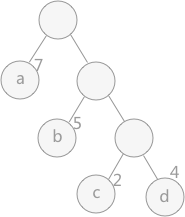
圖1 哈夫曼樹

什么是哈夫曼樹

當用 n 個結點（都做葉子結點且都有各自的權值）試圖構建一棵樹時，如果構建的這棵樹的帶權路徑長度最小，稱這棵樹為“最優二叉樹”，有時也叫“赫夫曼樹”或者“哈夫曼樹”。

在構建哈弗曼樹時，要使樹的帶權路徑長度最小，只需要遵循一個原則，那就是：權重越大的結點離樹根越近。在圖 1 中，因為結點 a 的權值最大，所以理應直接作為根結點的孩子結點。

構建哈夫曼樹的過程

對于給定的有各自權值的 n 個結點，構建哈夫曼樹有一個行之有效的辦法：

1. 在 n 個權值中選出兩個最小的權值，對應的兩個結點組成一個新的二叉樹，且新二叉樹的根結點的權值為左右孩子權值的和；
2. 在原有的 n 個權值中刪除那兩個最小的權值，同時將新的權值加入到?n–2 個權值的行列中，以此類推；
3. 重復 1 和 2 ，直到所以的結點構建成了一棵二叉樹為止，這棵樹就是哈夫曼樹。

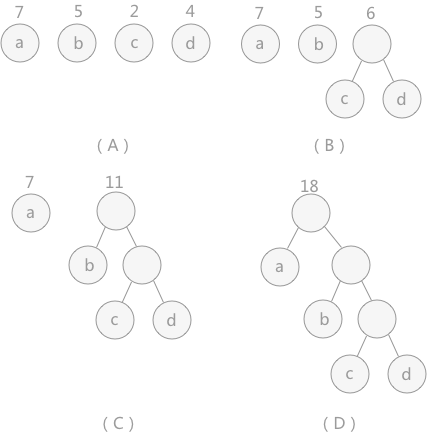
圖 2 哈夫曼樹的構建過程
?

圖 2 中，（A）給定了四個結點a，b，c，d，權值分別為7，5，2，4；第一步如（B）所示，找出現有權值中最小的兩個，2 和 4 ，相應的結點 c 和 d 構建一個新的二叉樹，樹根的權值為 2 + 4 = 6，同時將原有權值中的 2 和 4 刪掉，將新的權值 6 加入；進入（C），重復之前的步驟。直到（D）中，所有的結點構建成了一個全新的二叉樹，這就是哈夫曼樹。

哈弗曼樹中結點結構

構建哈夫曼樹時，首先需要確定樹中結點的構成。由于哈夫曼樹的構建是從葉子結點開始，不斷地構建新的父結點，直至樹根，所以結點中應包含指向父結點的指針。但是在使用哈夫曼樹時是從樹根開始，根據需求遍歷樹中的結點，因此每個結點需要有指向其左孩子和右孩子的指針。

所以，哈夫曼樹中結點構成用代碼表示為：

1. //哈夫曼樹結點結構
2. typedef struct {
3. int weight;//結點權重
4. int parent, left, right;//父結點、左孩子、右孩子在數組中的位置下標
5. }HTNode, *HuffmanTree;

構建哈弗曼樹的算法實現

構建哈夫曼樹時，需要每次根據各個結點的權重值，篩選出其中值最小的兩個結點，然后構建二叉樹。

查找權重值最小的兩個結點的思想是：從樹組起始位置開始，首先找到兩個無父結點的結點（說明還未使用其構建成樹），然后和后續無父結點的結點依次做比較，有兩種情況需要考慮：

• 如果比兩個結點中較小的那個還小，就保留這個結點，刪除原來較大的結點；
• 如果介于兩個結點權重值之間，替換原來較大的結點；

實現代碼：

1. //HT數組中存放的哈夫曼樹，end表示HT數組中存放結點的最終位置，s1和s2傳遞的是HT數組中權重值最小的兩個結點在數組中的位置
2. void Select(HuffmanTree HT, int end, int *s1, int *s2)
3. {
4. int min1, min2;
5. //遍歷數組初始下標為 1
6. int i = 1;
7. //找到還沒構建樹的結點
8. while(HT[i].parent != 0 && i <= end){
9. i++;
10. }
11. min1 = HT[i].weight;
12. *s1 = i;
14. i++;
15. while(HT[i].parent != 0 && i <= end){
16. i++;
17. }
18. //對找到的兩個結點比較大小，min2為大的，min1為小的
19. if(HT[i].weight < min1){
20. min2 = min1;
21. *s2 = *s1;
22. min1 = HT[i].weight;
23. *s1 = i;
24. }else{
25. min2 = HT[i].weight;
26. *s2 = i;
27. }
28. //兩個結點和后續的所有未構建成樹的結點做比較
29. for(int j=i+1; j <= end; j++)
30. {
31. //如果有父結點，直接跳過，進行下一個
32. if(HT[j].parent != 0){
33. continue;
34. }
35. //如果比最小的還小，將min2=min1，min1賦值新的結點的下標
36. if(HT[j].weight < min1){
37. min2 = min1;
38. min1 = HT[j].weight;
39. *s2 = *s1;
40. *s1 = j;
41. }
42. //如果介于兩者之間，min2賦值為新的結點的位置下標
43. else if(HT[j].weight >= min1 && HT[j].weight < min2){
44. min2 = HT[j].weight;
45. *s2 = j;
46. }
47. }
48. }

注意：s1和s2傳入的是實參的地址，所以函數運行完成后，實參中存放的自然就是哈夫曼樹中權重值最小的兩個結點在數組中的位置。

構建哈弗曼樹的代碼實現如下：

1. //HT為地址傳遞的存儲哈夫曼樹的數組，w為存儲結點權重值的數組，n為結點個數
2. void CreateHuffmanTree(HuffmanTree *HT, int *w, int n)
3. {
4. if(n<=1) return; // 如果只有一個編碼就相當于0
5. int m = 2*n-1; // 哈夫曼樹總節點數，n就是葉子結點
6. *HT = (HuffmanTree) malloc((m+1) * sizeof(HTNode)); // 0號位置不用
7. HuffmanTree p = *HT;
8. // 初始化哈夫曼樹中的所有結點
9. for(int i = 1; i <= n; i++)
10. {
11. (p+i)->weight = *(w+i-1);
12. (p+i)->parent = 0;
13. (p+i)->left = 0;
14. (p+i)->right = 0;
15. }
16. //從樹組的下標 n+1 開始初始化哈夫曼樹中除葉子結點外的結點
17. for(int i = n+1; i <= m; i++)
18. {
19. (p+i)->weight = 0;
20. (p+i)->parent = 0;
21. (p+i)->left = 0;
22. (p+i)->right = 0;
23. }
24. //構建哈夫曼樹
25. for(int i = n+1; i <= m; i++)
26. {
27. int s1, s2;
28. Select(*HT, i-1, &s1, &s2);
29. (*HT)[s1].parent = (*HT)[s2].parent = i;
30. (*HT)[i].left = s1;
31. (*HT)[i].right = s2;
32. (*HT)[i].weight = (*HT)[s1].weight + (*HT)[s2].weight;
33. }
34. }

注意，如果使用此程序，對權重值分別為 2、8、7、6、5 的節點構建哈夫曼樹，最終效果如圖 4(A) 所示。但其實，圖 4(B) 中顯示的哈夫曼樹也滿足條件，這兩棵樹的帶權路徑長度相同。
?

圖 4 兩種哈夫曼樹

之所以使用此程序構建的哈夫曼樹，是圖 4(A) 而不是 4(B)，是因為在構建哈夫曼樹時，結點 2 和結點 5 構建的新的結點 7 存儲在動態樹組中位置，比權重值為 7 節點的存儲位置還靠后，所以，在程序繼續選擇兩個權值最小的結點時，直接選擇了的葉子結點 6 和 7 。