This is a quick and straight to the point introduction to Euclidean distance and cosine similarity with a focus on NLP.

這是對歐氏距離和余弦相似度的快速而直接的介紹，重點是NLP。

歐氏距離 (Euclidean Distance)

The Euclidean distance metric allows you to identify how far two points or two vectors are apart from each other.

歐幾里德距離度量標準可讓您確定兩個點或兩個向量彼此相距多遠。

Now suppose you are a high school student and you have three classes. A math class, a philosophy class, and a psychology class. You want to check the similarity between these classes based on the words your professors use in class. For the sake of simplicity, let’s consider these two words: “theory” and “harmony”. You could then create a table like this to record the occurrence of these words in each class:

現在假設您是一名高中生，您有3個班級。 數學課，哲學課和心理學課。 您想根據您的教授在課堂上使用的單詞來檢查這些課程之間的相似性。 為了簡單起見，讓我們考慮以下兩個詞：“理論”和“和諧”。 然后，您可以創建一個像這樣的表來記錄每個類中這些單詞的出現情況：

In this table, the word “theory” is repeated 60 times in math class, 20 times in philosophy class, and 25 times in psychology class whereas the word harmony is repeated 10, 40, and 70 times in math, philosophy, and psychology classes respectively. Let’s translate this data into a 2D plane.

在此表中，“理論”一詞在數學課中重復了60次，在哲學課中重復了20次，在心理學課中重復了25次，而在數學，哲學和心理學課中，“和諧”一詞重復了10、40和70次分別。 讓我們將此數據轉換為2D平面。

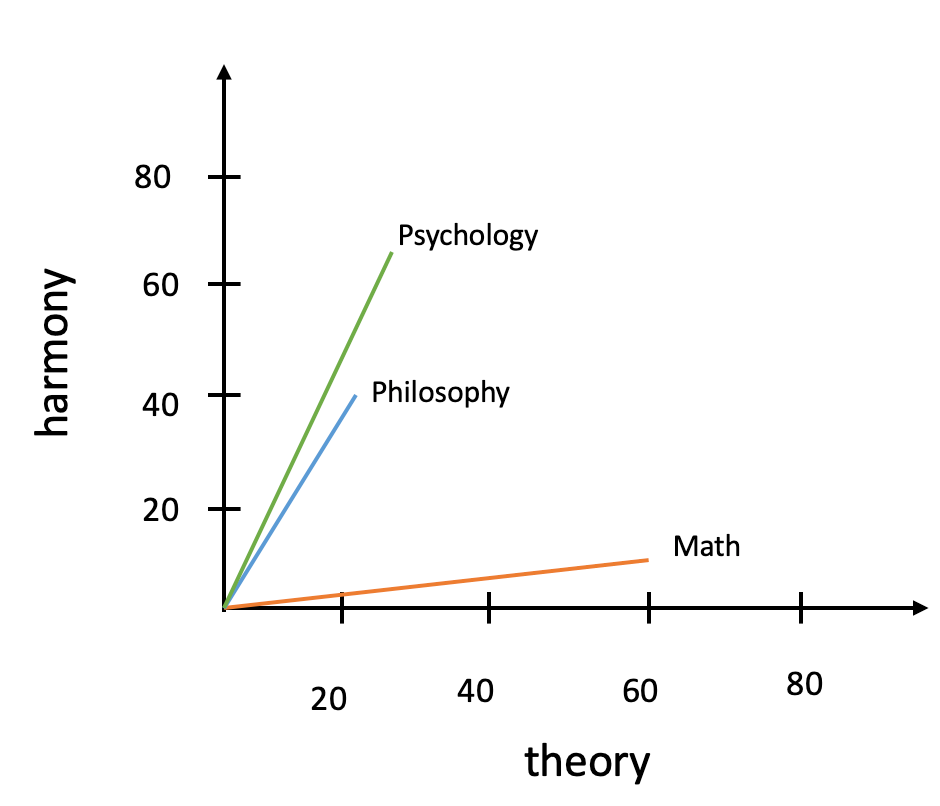
The Euclidean distance is simply the distance between the points. In the graph below.

歐幾里得距離就是點之間的距離。 在下圖中。

You can see clearly that d1 which is the distance between psychology and philosophy is smaller than d2 which is the distance between philosophy and math. But how do you calculate d1 and d2?

您可以清楚地看到，心理學與哲學之間的距離d1小于哲學與數學之間的距離d2。 但是，如何計算d1和d2？

The generic formula is the following.

通用公式如下。

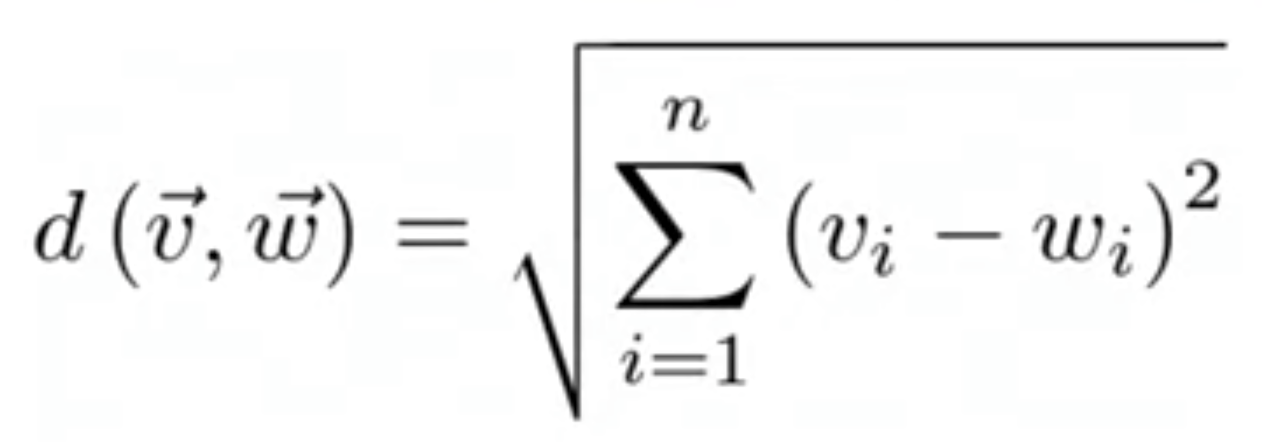
In our case, for d1, d(v, w) = d(philosophy, psychology)`, which is:

在我們的情況下，對于d1， d(v, w) = d(philosophy, psychology) `，即：

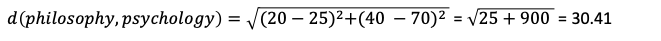
And d2

和d2

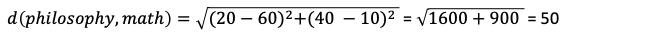
As expected d2 > d1.

如預期的那樣，d2> d1。

How to do this in python?

如何在python中做到這一點？

import numpy as np# define the vectorsmath = np.array([60, 10])philosophy = np.array([20, 40])psychology = np.array([25, 70])# calculate d1d1 = np.linalg.norm(philosophy - psychology)# calculate d2d2 = np.linalg.norm(philosophy - math)

余弦相似度 (Cosine Similarity)

Suppose you only have 2 hours of psychology class per week and 5 hours of both math class and philosophy class. Because you attend more of these two classes, the occurrence of the words “theory” and “harmony” will be greater than for the psychology class. Thus the updated table:

假設您每周只有2個小時的心理學課，而數學課和哲學課則只有5個小時。 由于您參加這兩個課程中的更多課程，因此“理論”和“和諧”一詞的出現將比心理學課程中的要大。 因此，更新后的表：

And the updated 2D graph:

以及更新后的2D圖形：

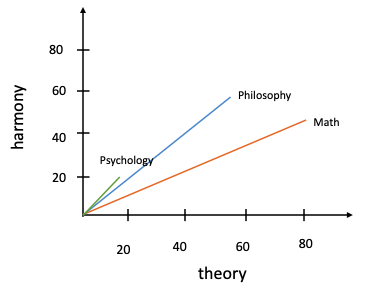
Using the formula we’ve given earlier for Euclidean distance, we will find that, in this case, d1 is greater than d2. But we know psychology is closer to philosophy than it is to math. The frequency of the courses, trick the Euclidean distance metric. Cosine similarity is here to solve this problem.

使用我們先前給出的歐幾里得距離公式，我們會發現，在這種情況下，d1大于d2。 但是我們知道心理學比數學更接近于哲學。 課程的頻率欺騙歐幾里德距離度量標準。 余弦相似度在這里解決了這個問題。

Instead of calculating the straight line distance between the points, cosine similarity cares about the angle between the vectors.

余弦相似度關心的是矢量之間的角度，而不是計算點之間的直線距離。

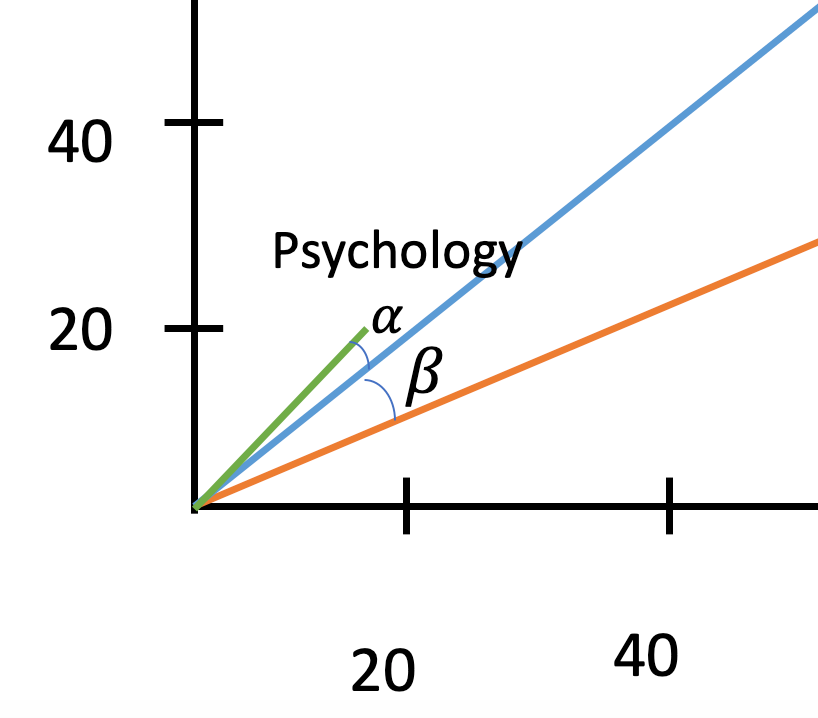
Zooming in on the graph, we can see that the angle α, is smaller than the angle β. That’s all cosine similarity wants to know. In other words, the smaller the angle, the closer the vectors are to each other.

放大該圖，我們可以看到角度α小于角度β。 這就是所有余弦相似度想要知道的。 換句話說，角度越小，向量彼此越接近。

The generic formula goes as follows

通用公式如下

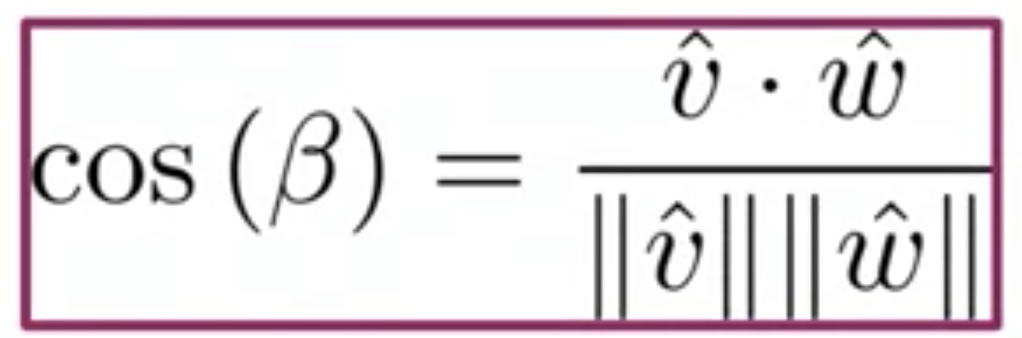
β is the angle between the vectors philosophy (represented by v) and math (represented by w).

β是向量原理(用v表示)和數學(用w表示)之間的夾角。

Whereas cos(alpha) = 0.99 which is higher than cos(beta) meaning philosophy is closer to psychology than it is to math.

而cos(alpha) = 0.99 (高于cos(beta)意味著哲學比數學更接近心理學。

Recall that

回想起那個

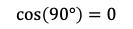
and

和

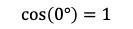
This implies that the smaller the angle, the greater your cosine similarity will be and the greater your cosine similarity, the more similar your vectors are.

這意味著角度越小，您的余弦相似度就越大，并且您的余弦相似度越大，向量就越相似。

Python implementation

Python實現

import numpy as npmath = np.array([80, 45])philosophy = np.array([50, 60])psychology = np.array([15, 20])cos_beta = np.dot(philosophy, math) / (np.linalg.norm(philosophy) * np.linalg.norm(math))print(cos_beta)

帶走 (Takeaway)

I bet you should know by now how Euclidean distance and cosine similarity works. The former considers the straight line distance between two points whereas the latter cares about the angle between the two vectors in question.

我敢打賭，您現在應該知道歐幾里得距離和余弦相似度是如何工作的。 前者考慮了兩個點之間的直線距離，而后者則考慮了所討論的兩個向量之間的角度。

Euclidean distance is more straightforward and is guaranteed to work whenever your features distribution is balanced. But most of the time, we deal with unbalanced data. In such cases, it’s better to use cosine similarity.

歐幾里得距離更簡單明了，并且可以保證只要要素分布平衡就可以使用。 但是大多數時候，我們處理不平衡的數據。 在這種情況下，最好使用余弦相似度。