5939. 半徑為 k 的子數組平均值

給你一個下標從 0 開始的數組 nums ，數組中有 n 個整數，另給你一個整數 k 。

半徑為 k 的子數組平均值 是指：nums 中一個以下標 i 為 中心 且 半徑 為 k 的子數組中所有元素的平均值，即下標在 i - k 和 i + k 范圍（含 i - k 和 i + k）內所有元素的平均值。如果在下標 i 前或后不足 k 個元素，那么 半徑為 k 的子數組平均值 是 -1 。

構建并返回一個長度為 n 的數組 avgs ，其中 avgs[i] 是以下標 i 為中心的子數組的 半徑為 k 的子數組平均值 。

x 個元素的 平均值 是 x 個元素相加之和除以 x ，此時使用截斷式 整數除法 ，即需要去掉結果的小數部分。

例如，四個元素 2、3、1 和 5 的平均值是 (2 + 3 + 1 + 5) / 4 = 11 / 4 = 3.75，截斷后得到 3 。

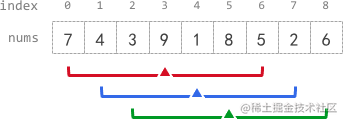
示例 1：輸入：nums = [7,4,3,9,1,8,5,2,6], k = 3
輸出：[-1,-1,-1,5,4,4,-1,-1,-1]
解釋：
- avg[0]、avg[1] 和 avg[2] 是 -1 ，因為在這幾個下標前的元素數量都不足 k 個。
- 中心為下標 3 且半徑為 3 的子數組的元素總和是：7 + 4 + 3 + 9 + 1 + 8 + 5 = 37 。使用截斷式 整數除法，avg[3] = 37 / 7 = 5 。
- 中心為下標 4 的子數組，avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4 。
- 中心為下標 5 的子數組，avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4 。
- avg[6]、avg[7] 和 avg[8] 是 -1 ，因為在這幾個下標后的元素數量都不足 k 個。示例 2：輸入：nums = [100000], k = 0
輸出：[100000]
解釋：
- 中心為下標 0 且半徑 0 的子數組的元素總和是：100000 。avg[0] = 100000 / 1 = 100000 。示例 3：輸入：nums = [8], k = 100000
輸出：[-1]
解釋：
- avg[0] 是 -1 ，因為在下標 0 前后的元素數量均不足 k 。

提示：

• n == nums.length
• 1 <= n <= $10^5$
• 0 <= nums[i], k <= $10^5$

解題思路

使用前綴和，可以快速計算出下標在 i - k 和 i + k 范圍（含 i - k 和 i + k）內所有元素的總和，計算公式為：pre[i+k]-pre[i-k-1]，如果在下標 i 前或后不足 k 個元素，則直接跳過該半徑為 k 的子數組平均值 的計算。

代碼

class Solution {
public:vector<int> getAverages(vector<int> &nums, int k) {int n = nums.size(),cnt=2*k+1;vector<long long > pre(n);vector<int> res(n,-1);pre[0]=nums[0];for (int i = 1; i < n; i++) {pre[i]=pre[i-1]+nums[i];}if (2*k<n)res[k]=pre[2*k]/cnt;for (int i = k+1; i+k < n; ++i) {res[i]=(pre[i+k]-pre[i-k-1])/cnt;}return res;}
};