層次聚類
層次聚類的概念:
層次聚類是一種很直觀的算法。顧名思義就是要一層一層地進行聚類。
層次法(Hierarchicalmethods)先計算樣本之間的距離。每次將距離最近的點合并到同一個類。然后,再 計算類與類之間的距離,將距離最近的類合并為一個大類。不停的合并,直到合成了一個類。其中類與類 的距離的計算方法有:最短距離法,最長距離法,中間距離法,類平均法等。比如最短距離法,將類與類 的距離定義為類與類之間樣本的最短距離。
層次聚類算法根據層次分解的順序分為:自下底向上和自上向下,即凝聚的層次聚類算法和分裂的層次聚 類算法(agglomerative和divisive),也可以理解為自下而上法(bottom-up)和自上而下法(top- down)
凝聚層次聚類的流程:
凝聚型層次聚類的策略是先將每個對象作為一個簇,然后合并這些原子簇為越來越大的簇,直到所有對 象都在一個簇中,或者某個終結條件被滿足。絕大多數層次聚類屬于凝聚型層次聚類,它們只是在簇間 相似度的定義上有所不同。
這里給出采用最小距離的凝聚層次聚類算法流程:
(1) 將每個對象看作一類,計算兩兩之間的最小距離;
(2) 將距離最小的兩個類合并成一個新類;
(3) 重新計算新類與所有類之間的距離;
(4) 重復(2)、(3),直到所有類最后合并成一類。
特點:
? 凝聚的層次聚類并沒有類似K均值的全局目標函數,沒有局部極小問題或是很難選擇初始點的問題。
? 合并的操作往往是最終的,一旦合并兩個簇之后就不會撤銷。
? 當然其計算存儲的代價是昂貴的。
層次聚類的優缺點:
優點:
1,距離和規則的相似度容易定義,限制少;
2,不需要預先制定聚類數;
3,可以發現類的層次關系;
4,可以聚類成其它形狀
缺點:
1,計算復雜度太高;
2,奇異值也能產生很大影響;
3,算法很可能聚類成鏈狀
代碼實現:
from scipy.cluster.hierarchy import dendrogram, linkage,fcluster
from matplotlib import pyplot as pltX = [[1,2],[3,2],[4,4],[1,2],[1,3]]
Z = linkage(X, 'ward')
f = fcluster(Z,4,'distance')
fig = plt.figure(figsize=(5, 3))
dn = dendrogram(Z) #層級聚類結果以樹狀圖表示出來并保存
print(Z)
plt.show()代碼解讀:
1.linkage(X, 'ward')
函數功能:進行層次聚類/凝聚聚類
linkage(y, method=’single’, metric=’euclidean’) 共包含3個參數:
(1) y是距離矩陣,可以是1維壓縮向量(距離向量),也可以是2維觀測向量(坐標矩陣)。
若y是1維壓縮向量,則y必須是n個初始觀測值的組合,n是坐標矩陣中成對的觀測值。
(2)method是指計算類間距離的方法。
method = ‘single’
d(u,v) = min(dist(u[i],u[j]))
對于u中所有點i和v中所有點j。這被稱為最近鄰點算法。
method = 'complete’
d(u,v) = max(dist(u[i],u[j]))
對于u中所有點i和v中所有點j。這被稱為最近鄰點算法。
method = 'average’
|u|,|v|是聚類u和v中元素的的個數,這被稱為UPGMA算法(非加權組平均)法。
method = 'weighted’
d(u,v) = (dist(s,v) + dist(t,v))/2
u是由s和t形成的,而v是森林中剩余的聚類簇,這被稱為WPGMA(加權分組平均)法。
method = ‘ward’ (沃德方差最小化算法)
新的輸入d(u,v)通過下式計算得出:
u是s和t組成的新的聚類,v是森林中未使用的聚類。T = |v|+|s|+|t|,|*|是聚類簇中觀測值的個數
參考來源聚類算法(五)——層次聚類 linkage (含代碼)
2.fcluster(Z,4,'distance')
fcluster(Z, t, criterion=’inconsistent’, depth=2, R=None, monocrit=None)
(1)第一個參數Z是linkage得到的矩陣,記錄了層次聚類的層次信息;
(2)t是一個聚類的閾值。
Z代表了利用“關聯函數”關聯好的數據。
比如上面的調用實例就是使用歐式距離來生成距離矩陣,并對矩陣的距離取平均
這里可以使用不同的距離公式
t這個參數是用來區分不同聚類的閾值,在不同的criterion條件下所設置的參數是不同的。
比如當criterion為’inconsistent’時,t值應該在0-1之間波動,t越接近1代表兩個數據之間的相關性越大,t越趨于0表明兩個數據的相關性越小。這種相關性可以用來比較兩個向量之間的相關性,可用于高維空間的聚類
depth 代表了進行不一致性(‘inconsistent’)計算的時候的最大深度,對于其他的參數是沒有意義的,默認為2
criterion這個參數代表了判定條件,這里詳細解釋下各個參數的含義:
(1)當criterion為’inconsistent’時,t值應該在0-1之間波動,t越接近1代表兩個數據之間的相關性越大,t越趨于0表明兩個數據的相關性越小。這種相關性可以用來比較兩個向量之間的相關性,可用于高維空間的聚類
(2)當criterion為’distance’時,t值代表了絕對的差值,如果小于這個差值,兩個數據將會被合并,當大于這個差值,兩個數據將會被分開。
(3)當criterion為’maxclust’時,t代表了最大的聚類的個數,設置4則最大聚類數量為4類,當聚類滿足4類的時候,迭代停止
(4)當criterion為’monocrit’時,t的選擇不是固定的,而是根據一個函數monocrit[j]來確定。
參考來源python的scipy層次聚類參數詳解
結果展示:
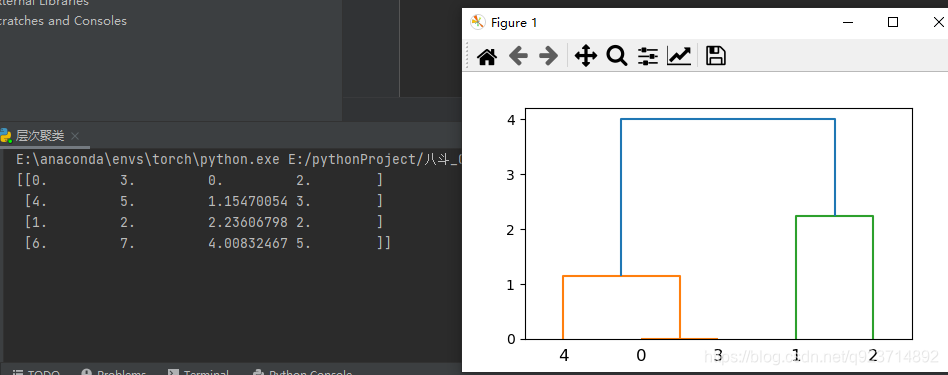
結果解讀:


第三行、第四行以此類推, 因為類別5有兩個樣本,加上類別4形成類別6,有3個樣本;
類別7是類別1、2聚類形成,有兩個樣本;
類別6、7聚成一類后,類別8有5個樣本,這樣X全部樣本參與聚類,聚類完成。
Z第四列中有樣本的個數,當最下面一行中的樣本數達到樣本總數時,聚類就完成了。
想分兩類時,就從上往下數有兩根豎線時進行切割,那么所對應的豎線下面所連接的為一類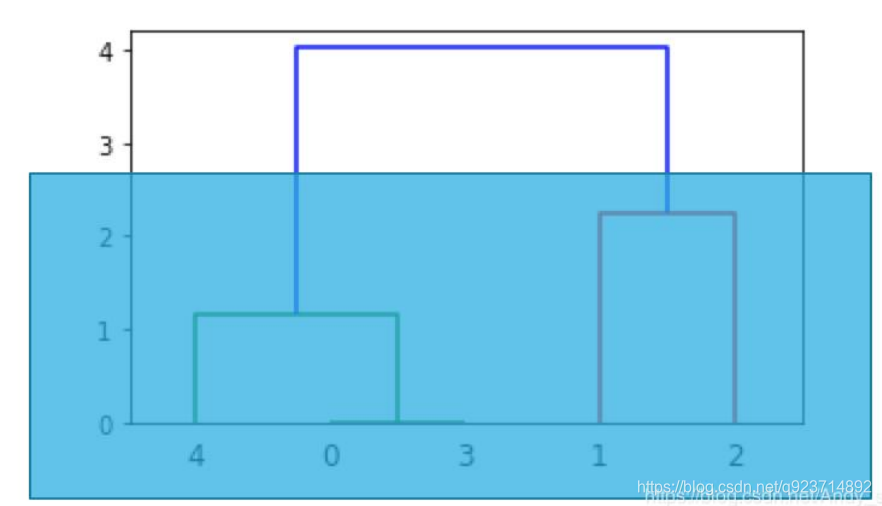
想分三類時,就從上往下數有三根豎線時進行切割,那么所對應的豎線下面所連接的為一類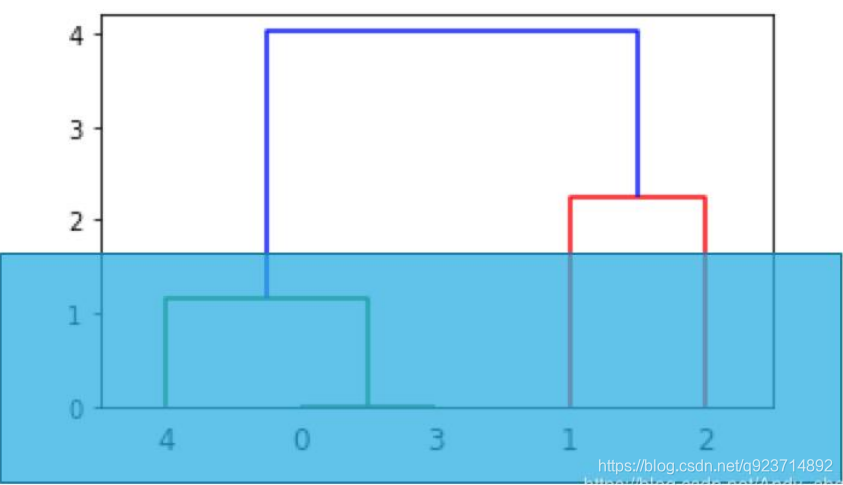
每一種聚類方法都有其特定的數據結構,對于服從高斯分布的數據用K-Means來進行聚類效果 會比較好。 而對于類別之間存在層結構的數據,用層次聚類會比較好。
密度聚類
密度聚類算法思想:
需要兩個參數:ε (eps) 和形成高密度區域所需要的最少點數 (minPts)
? 它由一個任意未被訪問的點開始,然后探索這個點的 ε-鄰域,如果 ε-鄰域里有足夠的點,則建立一 個新的聚類,否則這個點被標簽為雜音。
? 注意,這個點之后可能被發現在其它點的 ε-鄰域里,而該 ε-鄰域可能有足夠的點,屆時這個點會被 加入該聚類中。
密度聚類的優缺點:
優點:
1.對噪聲不敏感;
2.能發現任意形狀的聚類。
缺點:
1.但是聚類的結果與參數有很大的關系;
2.用固定參數識別聚類,但當聚類的稀疏程度不同時,相同的判定標準可能會破壞聚類的自然結構, 即較稀的聚類會被劃分為多個類或密度較大且離得較近的類會被合并成一個聚類。
代碼實現:
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.cluster import DBSCANiris = datasets.load_iris()
X = iris.data[:, :4] # #表示我們只取特征空間中的4個維度
print(X.shape)
# 繪制數據分布圖
'''
plt.scatter(X[:, 0], X[:, 1], c="red", marker='o', label='see')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
plt.show()
'''dbscan = DBSCAN(eps=0.4, min_samples=9)
#eps是兩個點的距離不大于eps時為一類,min_samples是指每個類最少min_samples個點
dbscan.fit(X)
#對x進行聚類
label_pred = dbscan.labels_# 繪制結果
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
x2 = X[label_pred == 2]
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label0')
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label1')
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label2')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
plt.show() 結果展示:
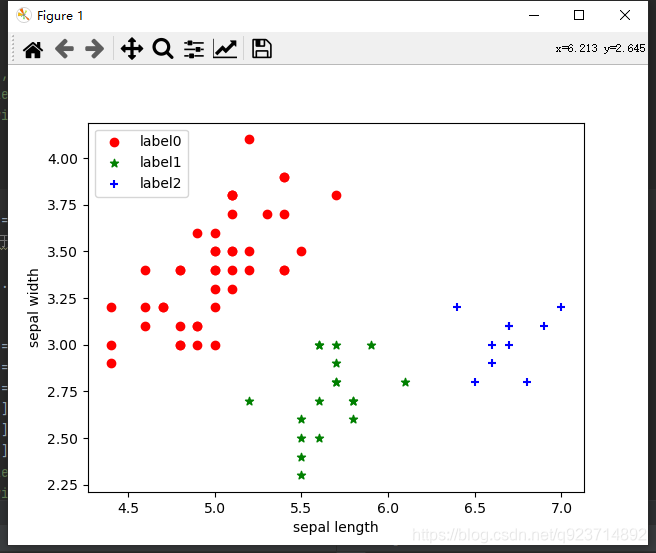
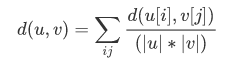
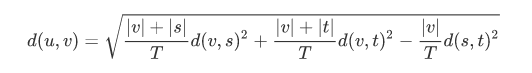







_主成分分析技巧)




![bzoj1095 [ZJOI2007]Hide 捉迷藏](http://pic.xiahunao.cn/bzoj1095 [ZJOI2007]Hide 捉迷藏)




思想及實現)

