統計 (Statistics)

I have read a few stories on Medium about writing advice, and there were some of them which, along with other tips, suggested that putting numbers in your story’s title will increase the number of views, as people tend to be more attracted by such headlines, and therefore, more people will click on your story.

我已經閱讀了有關“撰寫建議”的“媒體”上的一些故事，其中有一些故事以及其他技巧建議將數字放在故事標題中會增加觀看次數，因為人們通常會被此類標題吸引，因此會有更多人點擊您的故事。

It seems interesting that people are attracted by such headlines. But I don’t like to take things for granted. I want to convince myself that this fact is actually true.

人們被這樣的頭條新聞吸引似乎很有趣。 但是我不喜歡把事情當作理所當然。 我想說服自己，這個事實確實是真的。

So, what I have been thinking? Let’s use Statistics to check if this thing is actually true. But Statistics is useless without data. I first need to obtain some data about Medium articles and use that to do hypothesis testing. Therefore, I used Python and Beautiful Soup to scrape data about a random set of 6K+ Medium articles from 7 different publications. This dataset can be found on Kaggle. If you want to see how I scraped this data, I have an article about that here:

所以，我一直在想什么？ 讓我們使用統計信息來檢查這件事是否真的正確。 但是，如果沒有數據，統計信息將無用。 我首先需要獲取有關中型文章的一些數據，并使用這些數據進行假設檢驗。 因此，我使用Python和Beautiful Soup來刮取來自7個不同出版物的6K +中型隨機文章集的數據。 該數據集可以在Kaggle上找到。 如果您想了解如何抓取這些數據，請在此處發表有關此內容的文章：

What we are going to do now is to split this dataset into 2 groups (or samples): one that has numbers in headlines and one without numbers. Then, we will do a hypothesis test on the expected value for the number of claps in these 2 groups. We use the number of claps as a measure of “how successful” a story is, although a more logical variable for our scenario would be the number of views as it is the one that is more directly affected by our choice for the title. People typically click on a story because of the preview that they see (including headline and image), and then after they read the story, they decide whether to clap or not. But, because the number of views is not publicly shown on Medium, we use the number of claps as it should be highly correlated with views (the more the views, the more likely is that someone would clap).

現在，我們要做的就是將此數據集分為2組(或樣本)：一組在標題上有數字，而另一組沒有數字。 然后，我們將對這兩組的拍手數量的期望值進行假設檢驗。 我們使用拍手次數來衡量故事的“成功”程度，盡管對于我們的場景而言，更合乎邏輯的變量是觀看次數，因為觀看次數會直接受到我們對標題的選擇的影響。 人們通常會因為看到的預覽(包括標題和圖像)而點擊故事，然后在閱讀故事后決定是否拍手。 但是，由于視圖的數量未在“媒體”上公開顯示，因此我們使用拍手的數量，因為它應該與視圖高度相關(視圖越多，有人拍手的可能性就越大)。

If you are not familiar with hypothesis testing, here is an article you can read:

如果您不熟悉假設檢驗，則可以閱讀以下文章：

That being said, we will consider the following model:

話雖如此，我們將考慮以下模型：

Sample 1: Articles with numbers in headlines

示例1：標題中帶有數字的文章

We will model the number of claps inside this group as n i.i.d. (independent and identically distributed) random variables: X?, X?, …, X? with expected value μ? and variance σ?2, both of which are finite.

我們將這個組中拍手的數量建模為n iid(獨立且分布均勻)的隨機變量：X 1，X 2，…，X 1，其期望值為μ1，方差為σ2，這兩個都是有限的。

Sample 2: Articles without numbers in headlines

示例2：標題中沒有數字的文章

We will model the number of claps inside this group as m i.i.d. random variables: Y?, Y?, …, Y? with expected value μ? and variance σ?2, both of which are finite.

我們會為m IID隨機變量本組內拍手的次數型號：Y 1 Y 2，...，Y?與期望值μ?和方差σ?2，這兩者都是有限的。

We formulate the null hypothesis as “articles with numbers in headlines bring no improvement over articles that have no numbers in headlines”, and the alternative hypothesis as “articles with numbers in headlines are more successful compared to articles without numbers in headlines”.

我們將無效假設表述為“標題中帶有數字的文章與標題中沒有數字的文章沒有任何改進”，替代假設為“標題中帶有數字的文章比標題中沒有數字的文章更成功”。

Mathematically this means:

從數學上講，這意味著：

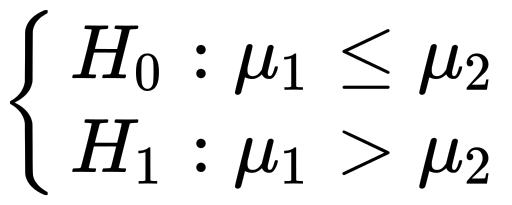
We will consider the following test statistic:

我們將考慮以下測試統計信息：

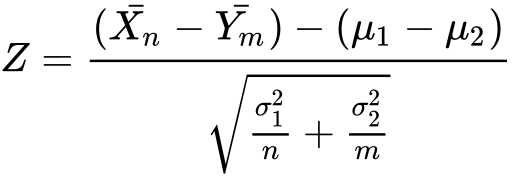
Where Xn bar and Ym bar are the averages of sample 1, respectively sample 2.

其中Xn bar和Ym bar是樣本1的平均值，分別是樣本2的平均值。

Because the sample sizes are pretty large and due to the Central Limit Theorem, the probability distribution of our test statistic Z can be approximated very well by a standard normal distribution, and the true variances σ?2, σ?2 should be very close to the estimated variances from our data. So, when we compute the test statistic, we can just substitute the estimated variances for σ?2, σ?2.

由于樣本量非常大并且由于中心極限定理，所以我們的測試統計量Z的概率分布可以通過標準正態分布很好地近似，并且真實方差σ?2，σ22應該非常接近于估計的方差我們的數據。 因此，當我們計算檢驗統計量時，我們可以僅將估計方差替換為σ?2，σ22。

But, what about μ? - μ?? By assuming H? to be true, it follows that μ? - μ? ≤ 0. And we choose μ? - μ? = 0 as this value is the worst-case scenario for the probability of type I error (we don’t want to underestimate the error).

但是，μ?-μ2呢？ 通過假設H?為真，可得出μ?-μ2≤0。我們選擇μ?-μ2 = 0，因為該值是I型錯誤概率的最壞情況(我們不想低估該錯誤) )。

Now, let’s run some Python code. We start by importing the required packages and defining a utility function: like(x, pattern). This function is used to match regular expressions in pandas data frames; x is the column, and pattern is a regular expression. I named this function after SQL’s LIKE operator as it is meant to do something similar, but for pandas data frames.

現在，讓我們運行一些Python代碼。 我們首先導入所需的包并定義一個實用程序函數： like(x, pattern) 。 該函數用于匹配熊貓數據幀中的正則表達式。 x是列，而pattern是正則表達式。 我將此函數命名為SQL的LIKE運算符，因為它的意思是做類似的事情，但適用于熊貓數據幀。

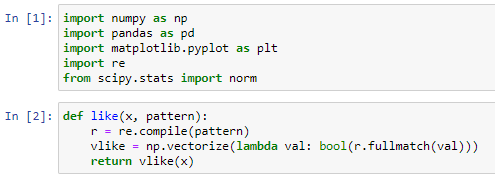
After that, we read the CSV file into a pandas data frame:

之后，我們將CSV文件讀入pandas數據框中：

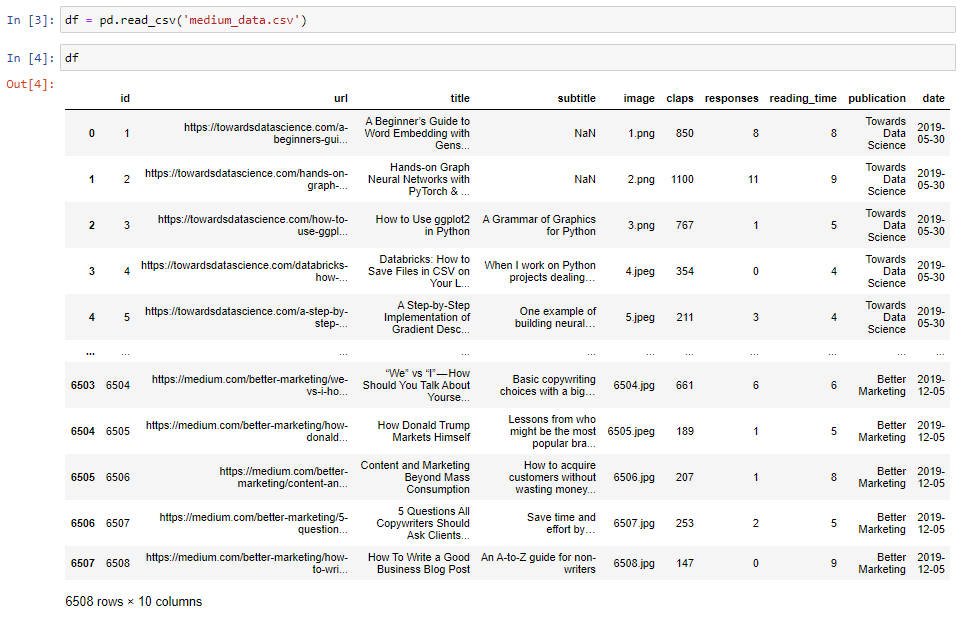
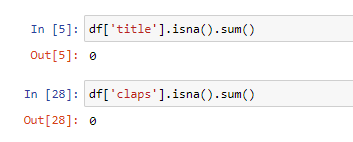
We make sure we don’t have missing values in the “title” or “claps” columns:

我們確保在“標題”或“拍子”列中沒有缺失的值：

Then, we create 2 new data frames (numbers/no-numbers) using the like() function defined earlier:

然后，我們使用前面定義的like()函數創建2個新的數據幀(數字/無數字)：

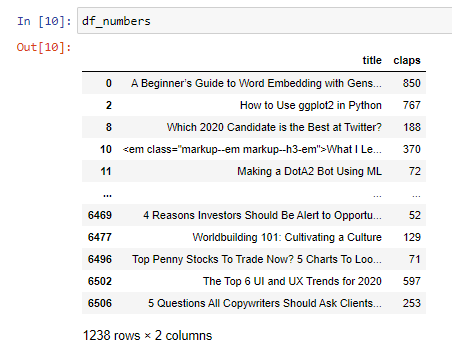
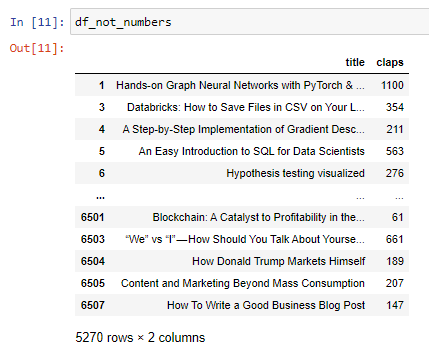
These 2 new data frames are shown below:

這兩個新數據幀如下所示：

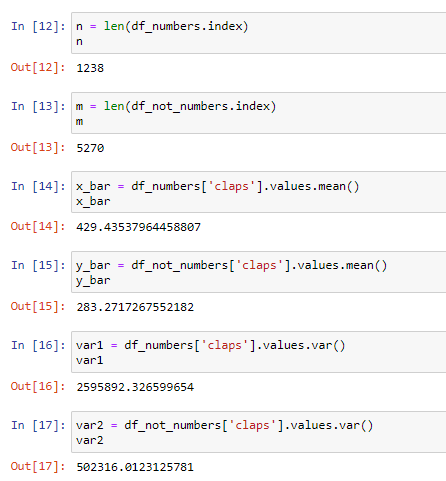
After that, we compute the quantities that we need for the test statistic:

之后，我們計算測試統計所需的數量：

Now, we compute the test statistic and the p-value. In our case, because we’re doing a one-sided test, the p-value is the area to the right of our test statistic under a standard gaussian:

現在，我們計算檢驗統計量和p值。 在我們的例子中，因為我們正在進行單面測試，所以p值是標準高斯下測試統計量右側的面積：

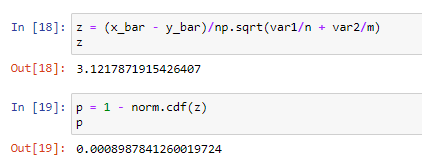
And we got a p-value much smaller than the usual threshold of 0.05. That’s good news, we can reject the null hypothesis very confidently.

而且我們得到的p值比通常的閾值0.05小得多。 這是個好消息，我們可以非常有信心地拒絕原假設。

For a significance level of α = 0.001, it follows that p ≈ 0.0009 < α, and therefore we reject the null hypothesis and accept the alternative. In plain English, this means: “We are 99.9% confident that stories with numbers in their headlines are expected to have more claps than stories without numbers in headlines”.

對于顯著性水平α= 0.001，可以得出p≈0.0009 <α，因此我們拒絕零假設并接受替代假設。 用簡單的英語來說，這意味著：“ 我們相信99.9％的人相信標題中帶有數字的故事比標題中沒有數字的故事更有拍手聲 ”。

You can find the Jupyter notebook on Kaggle.

您可以在Kaggle上找到Jupyter筆記本。

Thanks for reading!

謝謝閱讀！