I’m going to try something a little different today, in which I combine two (completely unrelated) topics I love talking about, and hopefully create something that is interesting and educational.

今天，我將嘗試一些與眾不同的東西，其中我結合了兩個我喜歡談論的主題(完全不相關)，并希望創建一些有趣且具有教育意義的東西。

…Actually, scratch that. If you’ve ever read anything I’ve written on Medium, this is actually pretty on brand (Explaining Linear Regression to Michael Scott, anyone?) In today’s article, I am going to explain what confidence intervals are, how to calculate them, and how to interpret them — all through the use case of Harry Potter’s infamous Divination teacher.

…實際上，把它刮掉。 如果您曾經讀過我在Medium上寫過的任何文章，那么實際上這在品牌上是很??不錯的( 向Michael Scott解釋線性回歸 ，有人嗎？)在今天的文章中，我將解釋什么是置信區間，如何計算它們，以及如何解釋它們-全部以哈利·波特臭名昭著的占卜老師為例。

For those of you who are unfamiliar with Harry Potter and Sybill Trelawney (which I’m assuming is nobody currently reading this, because it means you’ve been without internet for 20+ years), she is a witch who can “see into the future” through 99% educated guessing and 1% true prophecies. Confidence intervals, at least in my opinion, are pretty similar: making educated guesses about entire populations based on a small set of observations. However, instead of crystal balls and tea leaves, our tools are standard deviations and sample means.

對于不熟悉哈利·波特(Harry Potter)和西比爾·特勞拉尼(Sybill Trelawney)(我認為目前沒有人讀這本書，因為這意味著您已經有20多年沒有互聯網了)的那些人，她是一個巫婆，可以“觀察未來”通過99％的有根據的猜測和1％的真實預言。 至少在我看來，置信區間非常相似：根據一小組觀察結果對整個人群進行有根據的猜測。 但是，我們的工具不是標準的球和茶葉，而是水晶球和茶葉。

什么是置信區間，為什么人們使用它們？ (What is a Confidence Interval, and Why do People Use Them?)

Professor Trelawney has had thousands of students during her tenure at Hogwarts, and Dumbledore is doing an audit of her work to see how accurate she really is at predicting the future. However, Dumbledore is a busy guy (trying to hunt down Horcruxes and run a school) and can’t reach out to every student who has ever taken Trelawney’s class. So instead, he randomly selects a sample of 300 previous students and asks them what percentage of her predictions have come true so far.

特里勞妮教授她在霍格沃茨任職期間，已經有成千上萬的學生，和鄧布利多正在做她的工作進行審核，看她真的是在預測未來如何準確。 但是，鄧布利多是個忙碌的人(試圖追捕Horcruxes并經營一所學校)，無法接觸到曾經參加過Trelawney課的每個學生。 因此，他取而代之的是，從300名以前的學生中隨機選擇一個樣本，并詢問他們到目前為止，她的預測中有多少百分比是正確的。

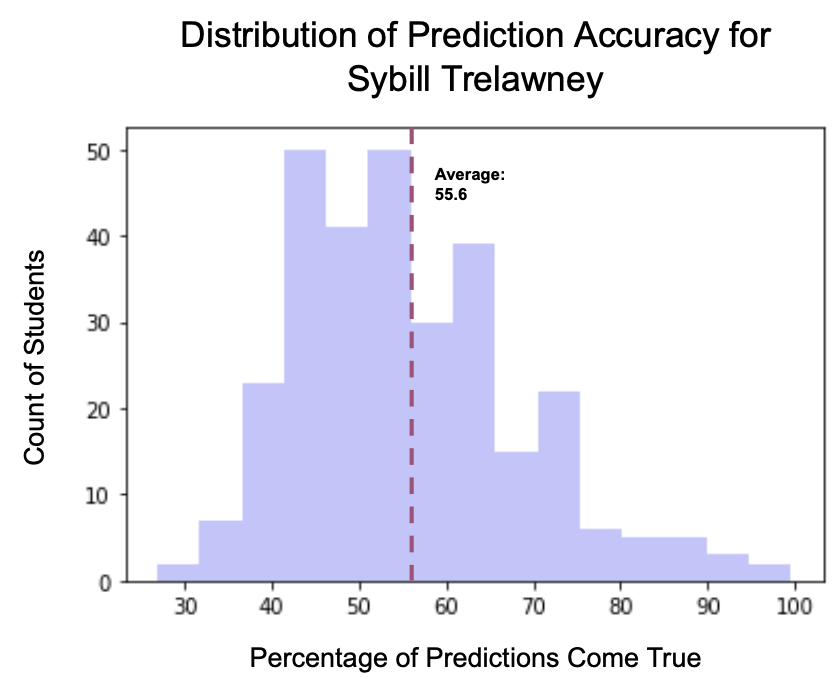
Dumbledore collects the responses and finds that the distribution of responses is left skewed, which means students are more likely to find Trelawney’s predictions to be inaccurate than accurate. In fact, the sample average is 55.6%, which means that Trelawney’s “predictions” are barely better than random guessing.

鄧布利多收集了答案，發現答案的分布是偏斜的，這意味著學生更有可能發現Trelawney的預測是不準確的，而不是準確的。 實際上，樣本平均值為55.6％，這意味著Trelawney的“預測”僅比隨機猜測好。

This is pretty concerning to Dumbledore, because he does not want a teacher who is essentially guessing when they teach Divination. He wonders what the true mean accuracy of her predictions is, and if it might actually be lower than the sample mean of 55.6% if he had reached out to every student she ever taught.

對于鄧布利多來說，這很令人擔憂，因為他不希望有一位在教授占卜術時實質上在猜測的老師。 他想知道她的預測的真正平均準確度是多少，如果他接觸過她曾經教過的每一個學生，那么它是否真的可能低于樣本平均水平55.6％。

Luckily, Dumbledore remembers a Muggle concept called the Central Limit Theorem (what can I say, he’s a multifaceted guy), which gives him the ability to approximate the true mean accuracy of Trelawney’s predictions. The Central Limit Theorem posits that when you have a sample of data and you want to find the true population statistic (i.e. a common example is mean so I will use it in this article, but it can be other measures as well), you can take smaller groups of the sample and find their mean (i.e. random samples of 30 people at a time, when you have a total sample of 300 people and total population of 30,000 people). If you have enough samples and the samples fulfill certain criteria, the sample means will fall into a normal distribution (regardless of the original distribution of the data) and the mean of the sampling distribution of the sample mean (I hate statistics sometimes) will approximate the true population mean (the mean, if you had actually surveyed all 30,000 people in the population).

幸運的是，鄧布利多記得一個麻瓜概念，即中心極限定理(我可以說，他是一個多面的人)，這使他能夠近似特雷勞尼的預測的真實平均準確度。 中心極限定理假設，當您有數據樣本并想要找到真實的總體統計量時(即，一個普通的例子是平均值，因此我將在本文中使用它，但也可以是其他度量)，您可以取較小的樣本組并找到平均值(即，當您的樣本總數為300人且總人口為30,000人時，一次隨機抽樣30人)。 如果您有足夠的樣本，并且樣本滿足某些條件，則樣本均值將落入正態分布(無論數據的原始分布如何)，并且樣本均值的采樣分布均值 (有時會討厭統計)真實人口均值(均值，如果您實際調查了人口中的所有30,000個人)。

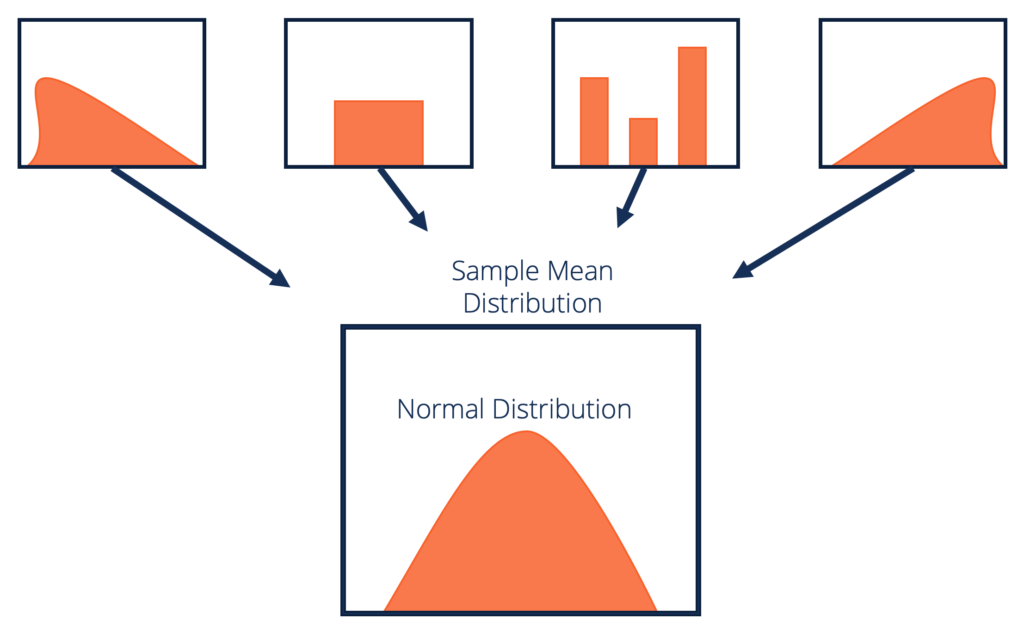
Based on this concept, Dumbledore knows that the 55.6% average accuracy is somewhere on the normally distributed curve of sample means, and the true accuracy is in the middle of this same distribution.

基于這樣的理念，鄧布利多知道，55.6％的平均準確度是某處的樣本均值的正態分布曲線上，而真正的精度在這相同的分布的中間。

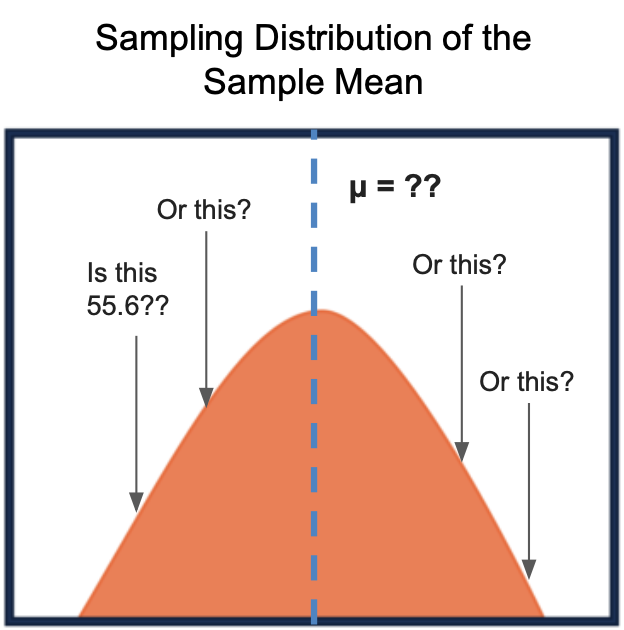
However, he still doesn’t know exactly where the sample mean lies on the distribution, and how close it is to the actual population mean (denoted as μ). This is where confidence intervals come in.

但是，他仍然不知道樣本均值在分布上的確切位置以及它與實際總體均值(表示為μ )有多接近。 這就是置信區間的來源。

Confidence intervals create an interval of standard deviations centered around the sample mean. Based on the size of the interval, you can declare that the interval will include the true population mean x% of the time. Many researchers and companies use 95% confidence intervals (span 2 standard deviations away from the sample mean on each side), but based on your use case, you can go higher or lower in confidence (i.e. 3 standard deviations away from the mean is 99.7% confidence).

置信區間創建一個以樣本平均值為中心的標準偏差區間。 根據時間間隔的大小，您可以聲明時間間隔將包括x時間的真實總體平均值。 許多研究人員和公司都使用95％的置信區間(距樣本均值2個標準偏差)，但是根據您的用例，您可以提高或降低置信度(即距均值3個標準偏差為99.7) ％ 置信度)。

Based on the example above, you can see how sample means that fall within 2 standard deviations of the population mean (inside the dark purple lines) will include the population mean (dotted blue line) in their 95% confidence interval. However, the sample means that are located more than 2 standard deviations from the population mean will not include the population mean in their confidence interval.

根據上面的示例，您可以看到樣本如何表示落入總體平均值的 2個標準偏差(深紫色線內)將在其95％置信區間內包括總體平均值(藍色虛線)。 但是，樣本均值與總體均值的差超過2個標準差時，不會在其置信區間內包括總體均值。

Since 95% of the values in a normal distribution reside within 2 standard deviations from the mean, we can be confident that 95% of the sample means will be within 2 standard deviations from the population mean. Following this, we can also say that 95% of all random samples taken from this population will include the true population mean in their 95% confidence interval.

由于正態分布中95％的值位于均值的2個標準差之內，因此我們可以確信95％的樣本均值將與總體均值在2個標準差之內。 之后，我們還可以說， 從該總體中抽取的所有隨機樣本中有95％將在其95％置信區間內包含真實總體平均值 。

如何計算置信區間 (How to Calculate a Confidence Interval)

Now that we have a general idea of what confidence intervals are used for and why they work, we can return to Hogwarts and help Dumbledore calculate the confidence interval for Professor Trelawney’s prediction accuracy.

既然我們對所用的置信區間及其工作原理有了一個大致的了解，我們可以返回霍格沃茨，并幫助鄧布利多計算特雷勞尼教授的預測準確性的置信區間。

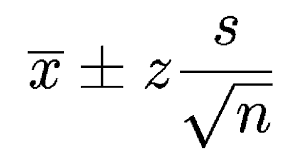
Above is the generic formula for calculating a confidence interval, where x? is the sample mean, z is the number of standard deviations from the mean we want the interval to span, s is the standard deviation of the sample, and n is the number of samples in the group.

上面是計算置信區間的通用公式，其中x?是樣本均值， z是相對于我們希望區間跨越的均值的標準偏差數， s是樣本的標準差， n是樣本數的標準差。組中的樣本。

The second half of the formula ( z * s / √n) calculates the actual value of what z standard deviations are (z = 2 for 95% confidence interval), and you add and remove this value from x? to find the upper and lower bound of your confidence interval.

公式的后半部分(z * s /√n)計算z標準差的實際值(對于95％置信區間， z = 2)，然后從x?中添加和刪??除該值以找到 置信區間的上限和下限。

If Dumbledore plugs in the assessment values into this formula, he will get:

如果Dumbledore將評估值插入此公式，他將得到：

Upper-bound

上限

= 55.6 + (2 x (12.9/√300)

= 55.6 +(2 x(12.9 /√300)

= 57.08%

= 57.08％

Lower-bound

下界

= 55.6 - (2 x (12.9/√300)

= 55.6-(2 x(12.9 /√300)

= 54.12%

= 54.12％

This means there is a good chance the true accuracy of Professor Trelawney’s prediction is between 54.12% — 57.08%. However, since Dumbledore only assessed one sample, we cannot say if this sample average (55.6%) was within 2 standard deviations of the population mean, and if its confidence interval successfully captured the true population average. There is a chance the sample average happened to be in the 5% of data that is > 2 standard deviations from the mean (aka one of the BAD BOIS in red below), and therefore completely missed the population mean.

這意味著特雷勞尼教授的預測的真實準確性很有可能在54.12％— 57.08％之間 。 但是，由于Dumbledore僅評估了一個樣本，因此我們無法確定該樣本平均值(55.6％)是否在總體均值的2個標準差之內，以及其置信區間是否成功捕獲了真實總體均值。 樣本平均值有可能在數據的5％內，與平均值相差> 2個標準差(也就是下面的紅色中的BAD BOIS之一)，因此完全錯過了總體平均值。

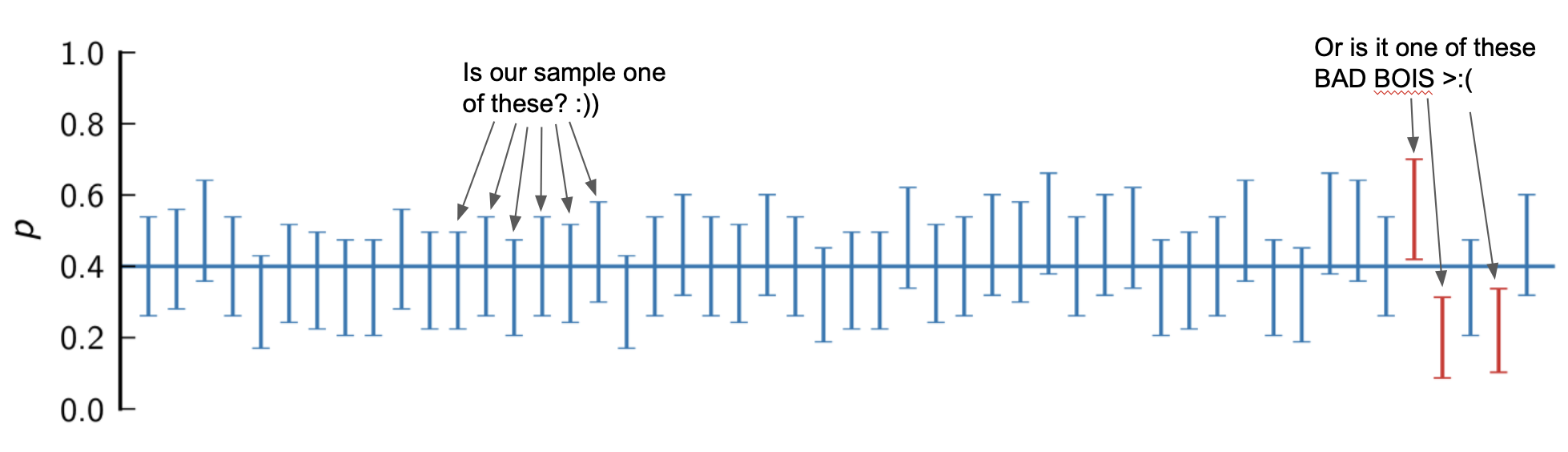
特雷勞尼教授的命運(又名鄧布利多的下一步) (Professor Trelawney’s Fate (aka Dumbledore’s next steps))

Dumbledore has a few options for next steps:

鄧布利多有幾個可供選擇的下一步：

1. He can send out the survey to a few more cohorts of 300 students each, and start plotting the cohort averages in a distribution. This will give him a better idea of where the 55.6% falls (i.e. close to the other values and likely within 2 standard deviations of the population mean, or significantly further from the other values and likely > 2 standard deviations).
   他可以將調查問卷發送給另外300個學生的隊列，然后開始在分布中繪制隊列平均值。 這將使他更好地了解55.6％的下降位置(即接近其他值，并且可能在總體均值的2個標準差內，或者比其他值明顯更遠，并且可能大于2個標準差)。
2. He can re-run the same analysis, this time taking smaller groups out of his 300 responses and plotting their means in a distribution (i.e. 100 random groups of 30 students each, with replacement). The mean of this distribution will give him a good idea of what the actual population mean is, without needing to use a confidence interval. A sample size of 30 (n=30) is the “rule-of-thumb” for the theorem of central tendency to work well, so Dumbledore actually went above and beyond with his original sample size of 300.
   他可以重新運行相同的分析，這次將他的300個響應中的較小的組從中抽取出來，并在分布中繪制平均值(即100個隨機組，每組30個學生，并有替換)。 該分布的平均值將使他對實際總體的平均值有一個很好的了解，而無需使用置信區間。 樣本大小為30(n = 30)是中心趨勢定理很好的“經驗法則”，因此鄧布利多實際上超過了他最初的樣本大小300。

Dumbledore considers his options, and decides to accept the confidence interval of 54.12% — 57.08% prediction accuracy for now. He is not terribly thrilled with the results, but he is relieved to see that the lower-bound of the interval is still greater than 50%, which means — at the very least — Professor Trelawney’s predictions are better than random guessing!

鄧布利多考慮了自己的選擇，決定暫時接受54.12％的置信區間-57.08％的預測準確度。 他對結果并不感到非常興奮，但看到該區間的下限仍然大于50％感到欣慰，這意味著-至少-至少，Trelawney教授的預測比隨機猜測要好！

He has summarized his findings, and will present them to Pressor Trelawney in her next performance review. Maybe he will recommend for her to add confidence intervals to her to her syllabus in the coming years 🧙🏼?♀?🔮

他總結了他的發現，并將在下一次性能評估中向Pressor Trelawney提出。 也許他會建議她在未來幾年為她的課程提綱增加信心intervals?🧙🏼?🔮