短時傅里葉變換及其逆變換

本篇文章主要記錄了使用python進行短時傅里葉變換，分析頻譜，以及通過頻譜實現在頻域內降低底噪的代碼及分析，希望可以給同樣在學習信號處理的大家一點幫助，也希望大家對我的文章多提意見建議。

一. 短時傅里葉變換與離散傅里葉變換

在這篇文章中我們主要運用了短時傅里葉變換，要想清楚地理解短時傅里葉變換，首先必須要了解離散傅里葉變換(Discrete Fourier Transform，DFT)。

1.離散傅里葉變換

離散傅里葉的定義:
$$?k\in [0,M?1],X[k]=\sum _{n=0}^{N?1}x[n]e^{?\frac{2j\pi n{f}_k}{F_e}}=\sum _{n=0}^{N?1}x[n]e^{?\frac{2j\pi nk\frac{F_e}{M}}{Fe}}$$
$={\sum }_{n=0}^{N?1}x[n]e^{?\frac{2j\pi kn}{M}}$

離散傅里葉變換適用于在時域上不連續且有限的數字信號，在上述公式中，x[n] 就是我們在時域中的初始數字信號，Fe 對應這個信號的采樣頻率。在離散傅里葉變換中，首先初始數字信號本身是離散的，在上式中初始信號x[n]是在時域內的一段有限信號，N代表了該段數字信號一共包含N個采樣點，即其在時域上的長度為1/Fe * N。同時離散傅里葉變換所得的結果X[k]在頻域上也是離散的，簡而言之，是將頻域[0,Fe]等分成了M份 :

X[k]也可以理解為包含了M個復數值的向量。在離散傅里葉變換中，采樣點的個數N(時域上的取樣長度)，以及頻域上的采樣個數M都是可調整的，兩個采樣個數的選擇對于DFT的解析度和精確度會有影響，這里就不過多展開。

我們在實際應用離散傅里葉變換時，會發現，有的時域上完全不同的信號，他們的離散傅里葉變換頻譜卻是一致的，因此我們引入一個新的 短時傅里葉變換(STFT)。

2.短時傅里葉變換

短時傅里葉變換的定義 :

$X(\tau ,f)={\int }_{R}x(t)h^{?}(t?\tau )e^{?2j\pi ft}dt$

其中，$h^{?}(t?\tau )$ 是一個中心為$\tau$的窗函數

當引入了時間變量$\tau$之后我們就可以針對不同瞬間進行頻譜分析，對于每一個瞬間$\tau$我們都可以獲取信號在該時刻的頻譜。

二. 使用python 進行短時傅里葉變換

在這一部分我會分享基于python的短時傅里葉變換的實現，可供參考。
首先是可能使用到的python庫

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import wavfile
from IPython.display import display, Audio
from numpy import log10

接下來就是短時傅里葉變換的python實現

def TFCT(trame, Fe, Nfft,fenetre,Nwin,Nhop):L = round((len(trame) - len(fenetre))/Nhop)+1M = Nfftxmat = np.zeros((M,L))print('xmat',xmat.shape)print(Nwin+Nhop)for j in range(L):xmat[:,j] = np.fft.fft(trame[j*Nhop:Nwin+Nhop*j]*fenetre,Nfft)  x_temporel = np.linspace(0,(1/Fe)*len(trame),len(trame))x_frequentiel = np.linspace(0, Fe,Nfft)return xmat,x_temporel,x_frequentiel

上述函數解釋:
參數部分
trame和Fe : 初始的數字信號和它的采樣頻率
Nfft : 上文提到的離散傅里葉變換中，頻域的采樣個數M
fenetre : 短時傅里葉變換中使用的窗函數，在接下來的實現中我都使用了漢明窗np.hamming。
Nwin : 窗函數的長度(包含點的個數)
Nhop : 窗函數每次滑動的長度，一般規定為Nwin/2，窗函數長度的一半

首先創建一個M行L列的矩陣xmat，該矩陣的每一行代表一個0-Fe的頻率，單位為Hz，每一列對應該段被窗函數截取的信號的FFT快速傅里葉變換。

三. 使用overlapp-add算法進行短時傅里葉變換的逆變換重構原信號

在這一部分中，我們使用了overlapp-add算法來進行短時傅里葉變換的逆變換。
下面是該部分的全部代碼，之后會逐步解釋算法的實現 :

def ITFD(xmat,Fe,Nfft,Nwin,Nhop):window = np.hamming(Nwin)Te = 1/Feyvect = np.zeros(Nfft + (xmat.shape[1]-1)*Nhop,dtype=complex)t_vecteur = np.arange(0,Te*len(yvect),Te)index = 0K = 0L = xmat.shape[1]yl = np.zeros(xmat.shape,dtype=complex)for j in range(L):yl[:,j] = np.fft.ifft(xmat[:,j])# 平移和求和for k in range(L):yvect[Nhop*k:Nfft+Nhop*k] += yl[:,k]# 標準化幅值for n in range(Nwin-1):K +=  window[n]K /= Nhopyvect /=Kreturn t_vecteur, yvect

該算法的實現需要三步。

1. 快速傅里葉逆變換

yl = np.zeros(xmat.shape,dtype=complex)
for j in range(L):yl[:,j] = np.fft.ifft(xmat[:,j])

第一步，對上一部分得出的矩陣xmat進行快速傅里葉變換的逆變換，得出同樣規格M行L列的矩陣yl。

2. 對各列進行平移并疊加

 # 平移和求和for k in range(L):yvect[Nhop*k:Nfft+Nhop*k] += yl[:,k]

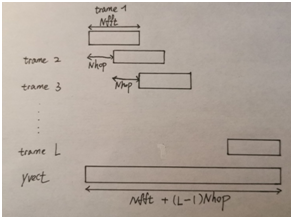
對yl矩陣的每一列平移 (l-1)Nhop，l $\in$ [1,L]，例如第一列不變，第二列平移Nhop，第三列平移2Nhop，以此類推。之后將所有列的轉置，疊加到總長度為Nfft +(L-1)*Nhop的向量yvect中。

3. 標準化

# 標準化幅值
for n in range(Nwin-1):K +=  window[n]K /= Nhopyvect /=K
return t_vecteur, yvect

window[n] (w[n]) 是長度為Nwin的窗函數，在選取窗函數的時候，我們總滿足規則 $$K=\sum _{l=1}^{L}w[n?(l?1)Nhop]$$ K的值與n無關。在此基礎上不難證明
$$K\approx \sum _{n=0}^{Nwin?1}w[n]/Nhop$$

那么通過以上的三個步驟，我們就可以從信號的短時傅里葉變換矩陣中完美重構原信號了。
下一篇文章我們將使用這些算法，使用譜減法進行聲音信號的降噪處理。