一文看懂計算機神經網絡與梯度下降

1. 計算機神經網絡與神經元

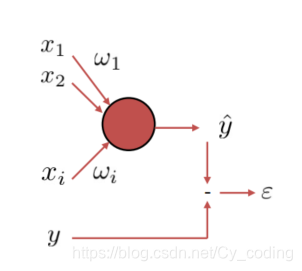
要理解神經網絡中的梯度下降算法，首先我們必須清楚神經元的定義。如下圖所示，每一個神經元可以由關系式 $f(\sum_{i=1}^nw_ix_i + b)$ 來描述，其中 $X = [x_1,x_2,...,x_n]$ 就是N維的輸入信號， $W =[w_1,w_2,...,w_n]$ 是與輸入向量一一對應的n維權重， $b$ bias 偏斜， $y$ 對應該神經元的輸出， $f$ 函數稱為激勵函數，例如sigmoid函數，softmax函數等等。

那么一個神經網絡是如何進行學習的呢？以一個神經元為例，在一組輸入信號 $X$ 經過該神經元后，我們得到了一個輸出信號稱之為 $y_{etoile}$ ，而訓練集中給出的實際輸出例如為 $y$ ，那么顯而易見地，想要提高正確率，即正確地學習對于一組輸入應該獲得的輸出 $y$ ，一個神經元所做的計算，就是一個最優化(最小化)問題，通過改變權重 $W$ 來最小化損失(誤差) $l(y,y_{etoile})$ 。當然，這個誤差的定義可以根據問題的不同有所區別，例如簡單的向量L1，L2距離，MSE均方誤差。對于整個訓練集而言，當然不止包含了一組輸入輸出。因此整體而言，誤差Loss Function $\frac{1} {N}\sum_{t=1}^{K}l(y_t,y_{t_{etoile}})$ 是所有K組訓練數據誤差的總和的平均數。

我們已經知道了，Loss Function損失函數與神經元的權重息息相關，神經元要做的計算，就是找到能最小化該損失函數的權重 $W$ 。優化的算法紛繁多樣，使用的較為廣泛的就是梯度下降 $gradientdescentgradient\space\space descent$ 及其衍生算法SGD隨機梯度下降，BGD批量梯度下降。

在這里插入圖片描述

2. 梯度下降算法 $gradientdescentgradient\space\space descent$

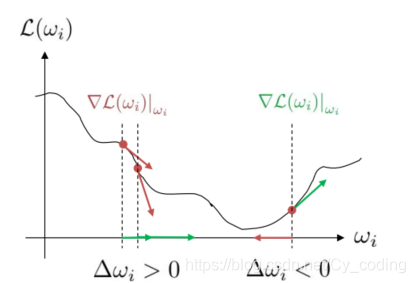
梯度下降算法，一言以蔽之，就是沿著梯度下降的方向不斷迭代，最終逼近函數最小值的優化方法。如下圖所示，在最小化Loss Function損失函數的過程中，權重總是沿著損失函數梯度下降的方向變化，即 $wi=wi?λ?L∣wiw_i = w_i - \lambda\nabla L|_{w_i}$ ，其中 $λ\lambda$ 為學習率。當損失函數的梯度接近0時，可以終止迭代。大致理解了梯度下降算法的原理，接下我們看看在優化神經元的過程中，梯度下降算法是如何實現的。

在這里插入圖片描述

3. backpropagation 反向傳播算法

通過上一個部分，我們理解了使權重沿著Loss的梯度下降方向迭代，可以最終最小化損失函數。這個過程中，權重的更新 $wi=wi?λ?L∣wiw_i = w_i - \lambda\nabla L|_{w_i}$ 取決于損失函數的梯度。計算該梯度的最常用方法，就是反向傳播算法。反向傳播算法其實際原理類似于復合函數導數。我們通過鏈式法則，可以將所需求的梯度分割成子變量的梯度的乘積。
以單個神經元的神經網絡的優化為例:
$yetoile=f(∑i=1nwixi+b)y_{etoile} = f(\sum_{i=1}^nw_ix_i + b)$

$e_i = w_ix_i$ ,

$v=∑iei+θv=\sum_ie_i+ \theta$

默認使用sigmoid激勵函數:

$yetoile=σ(v)y_{etoile} = \sigma(v)\space\space$ 經過激勵函數后的輸出

$σ(v)=11+e?v\sigma(v) = \frac{1}{1+e^{-v}}\space\space$ sigmoid函數

$?=yetoile?y\epsilon = y_{etoile} - y\space\space$ $y_{etoile}$ 與實際值 $y$ 的誤差

$\epsilon^2$

使用鏈式法則我們不難得到 :
$?L?wi=?L?ei?ei?wiwhere?ei?wi=xi\frac{\partial L}{\partial w_i} = \frac{\partial L}{\partial e_i}\frac{\partial e_i}{\partial w_i} \space\space where \space\frac{\partial e_i}{\partial w_i} = x_i$

$?L?ei=?L?v?v?eiwhere?v?ei=1\frac{\partial L}{\partial e_i} = \frac{\partial L}{\partial v}\frac{\partial v}{\partial e_i} \space\space where \space\frac{\partial v}{\partial e_i} =1$

$?L?v=?L?yetoile?yetoile?vwhere?yetoile?v=σ′(v)=e?v(1+e?v)2\frac{\partial L}{\partial v} = \frac{\partial L}{\partial y_{etoile}}\frac{\partial y_{etoile}}{\partial v} \space\space where \space\frac{\partial y_{etoile}}{\partial v} =\sigma'(v) = \frac{e^{-v}}{(1+e^{-v})^2}$

$?L?yetoile=?L?????yetoilewhere???yetoile=1\frac{\partial L}{\partial y_{etoile}} = \frac{\partial L}{\partial \epsilon}\frac{\partial \epsilon}{\partial y_{etoile}} \space\space where \space\frac{\partial \epsilon}{\partial y_{etoile}} =1$

最后， $?L??=2?\frac{\partial L}{\partial \epsilon} = 2\epsilon$

通過鏈式法則，我們將復雜的復合函數的梯度拆解為一個個基礎的梯度，他們的乘積就是我們需要的損失函數Loss Function關于權重的梯度:
$?L∣wi=2(?)σ′(v)xi\nabla L|_{w_i} = 2(\epsilon)\sigma'(v)x_i$

首先對于每個訓練集中的數據 $X$ ，以及對應的當前權重 $W$ ，我們首先通過正向傳播，計算出各個關鍵值并儲存在內存中。
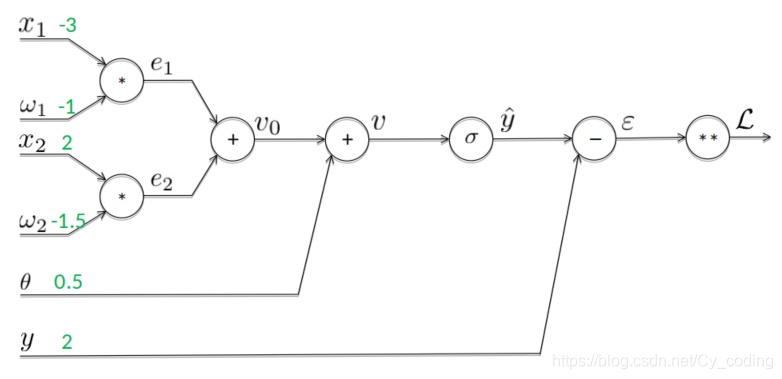
在這里插入圖片描述
如下所示，通過正向傳播以及各個變量之間的數值關系，我們可以很簡單地計算出每次迭代各個變量對應的值。

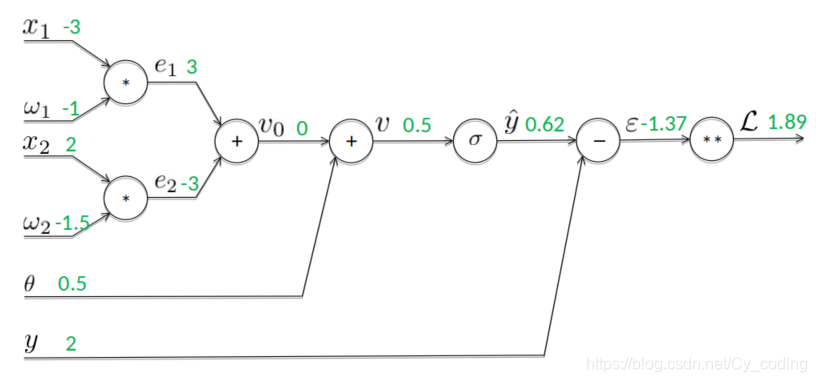
接著就是反向傳播計算梯度的過程了，如下圖所示，例如我們有 $?L??=2?=?1.37?2=?2.75\frac{\partial L}{\partial \epsilon} = 2\epsilon = -1.37 * 2 = -2.75$
又有
$???yetoile=1\frac{\partial \epsilon}{\partial y_{etoile}} =1$
因此
$?L?yetoile=?L?????yetoile=?2.75\frac{\partial L}{\partial y_{etoile}} = \frac{\partial L}{\partial \epsilon}\frac{\partial \epsilon}{\partial y_{etoile}} = -2.75$

…
依此類推，我們不難通過鏈式法則，一步一步反向傳播，直到計算出我們最終需求的梯度值: $?L?wi\frac{\partial L}{\partial w_i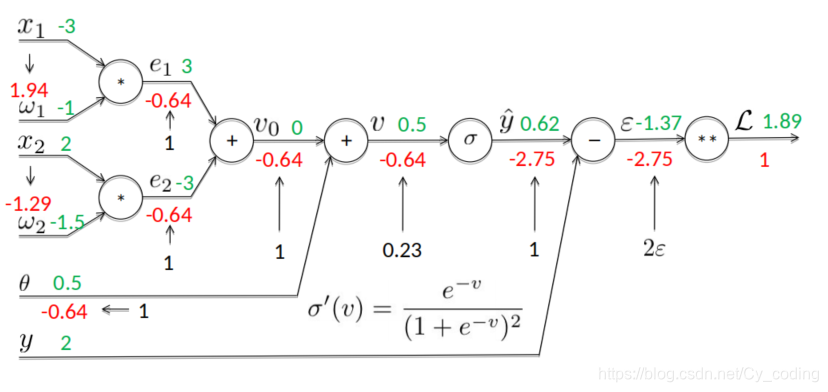}$ 在這里插入圖片描述
理解了梯度下降算法在訓練神經元過程中的應用，以及反向傳播算法如何計算出復合梯度的過程，接下來分享一個Tensorflow模塊中非常好用的計算梯度的類，這大大簡化了我們計算反向傳播的過程。

4. Tensorflow GradientTape

用幾個簡單的例子介紹一下功能強大的GradientTape類，可以幫助我們在深度學習中簡便地計算函數的梯度。

import tensorflow as tf
with tf.GradientTape(watch_accessed_variables=True) as t:x = tf.Variable(3.0)y = x ** 2# t.watch(x)dy_dx = t.gradient(y,x)print(type(dy_dx))print(dy_dx.numpy())print(dy_dx)

上述代碼計算了 $y = x^2$ 這個函數在 $x =$
輸出結果如下 :
在這里插入圖片描述
Tensorflow庫中的GradientTape類使用簡單，其中輸入輸出都推薦定義為張量tensor的形式，即可訓練的變量形式。GradientTape類中的watch_accessed_variables參數決定了類是否會自動觀測保存可訓練的變量，當這個參數值為False時，我們可以使用 t.watch()方法指定類觀察的具體變量。

如下例子，調用t.gradient()方法時，變量也可以是高維的tensor。

w = tf.Variable(tf.random.normal((3,2)),name='w')
b = tf.Variable(tf.zeros(2,dtype=tf.float32),name='b')
x = [[1.,2.,3.]]with tf.GradientTape() as tape:y = x @ w + bloss = tf.reduce_mean(y**2)# 可以用張量的形式同時計算多個變量tensor對應的梯度[dl_dw, dl_db] = tape.gradient(loss,[w,b])print(dl_dw)print(dl_db)

輸出結果如下:
在這里插入圖片描述
以我們在上一部分做的反向傳播算法為例 :

with tf.GradientTape() as tape:W = tf.Variable([[-1.,-1.5]])X = tf.Variable([[-3.],[2.]])thelta = tf.Variable(0.5,dtype=tf.float32)y_etoile = tf.sigmoid(W @ X + thelta)y = tf.Variable(2,dtype=tf.float32)loss = (y_etoile - y) ** 2(dl_dx, dl_dw, dl_dthe) = tape.gradient(loss,[X,W,thelta])print(dl_dw)

輸出結果如下:

可以看到，我們使用tensorflow計算出的梯度 $?L?wi\frac{\partial L}{\partial w_i}$ 與使用反向傳播算法的計算結果是一致的。
在這里插入圖片描述

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/386860.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/386860.shtml
英文地址，請注明出處：http://en.pswp.cn/news/386860.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！