
本文主要介紹了當前機器學習模型中廣泛應用的交叉熵損失函數與softmax激勵函數。
這個損失函數主要應用于多分類問題,用于衡量預測值與實際值之間的相似程度。
交叉熵損失函數定義如下: LCE(y^,y?)=?∑i=1Nclassesyi?log(yi^)L_{CE}(\hat{y}, y^*) = - \sum_{i=1}^{Nclasses} y_i^*log(\hat{y_i})LCE?(y^?,y?)=?i=1∑Nclasses?yi??log(yi?^?)
其中 y^\hat{y}y^? 為預測向量,y?y^*y?為真實標簽向量。在多分類問題機器學習中,y?y^*y? 一般使用獨熱編碼。例如,在一個三分類問題中, y?y^*y?向量的維度就是三維,對應屬于某一類則該位為1,其余位為0。第一類對應的真實標簽向量即為[1,0,0]T[1, 0, 0]^T[1,0,0]T,第二類對應的真實標簽向量為[0,1,0][0,1,0][0,1,0] 等等以此類推。
很顯然,對于這個損失函數而言,取到最小值的時候就是當求和部分取得最大值,即預測向量與標簽向量相似度最大時,其乘積也最大。以下圖為例,例如該類真實標簽為Class2,當向量y^\hat{y}y^?的第二項趨向于于1,此時損失函數取得最小值,我們也保證了預測值與真實值之間的誤差最小了。
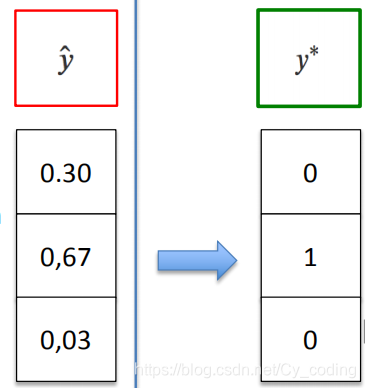
很顯然,這里我們有兩個問題,其一是為什么要使用預測值的log函數值與真實的標簽相乘而不直接使用兩者原始值相乘。其原因在于,由于我們的概率范圍總是在0-1之間,直接獲取乘積往往會使得不同的損失之間的差別不大,不利于我們進一步通過這個誤差來優化我們的模型。
第二個問題是,如何保證預測向量滿足概率分布。我們都知道標簽向量y?y^*y? 由于使用了獨熱編碼,因此他永遠滿足概率分布即∑p(x)=1\sum p(x) = 1∑p(x)=1,但是我們的預測向量 y^\hat{y}y^? 卻不一定。這里就要用到我們的softmax激勵函數了。簡單的來說,softmax函數就幫助我們將一個隨機數值的向量,轉化為了一個所有值在0-1之間,且和為1的向量,以滿足概率分布關系。softmax函數的定義如下: yt,k=e(yt,k)∑ke(yt,k)y_{t,k} = \frac{e^{(y_{t,k})}}{\sum_ke^{(y_{t,k})}}yt,k?=∑k?e(yt,k?)e(yt,k?)?
其中下標t對應第t個樣本,k對應輸出層的第k個神經元。softmax函數首先將所有輸出層神經元對應的值通過指數函數轉換為正值,再通過歸一化處理,除以他們的指數函數值之和,以保證所有項對應的值之和為1。
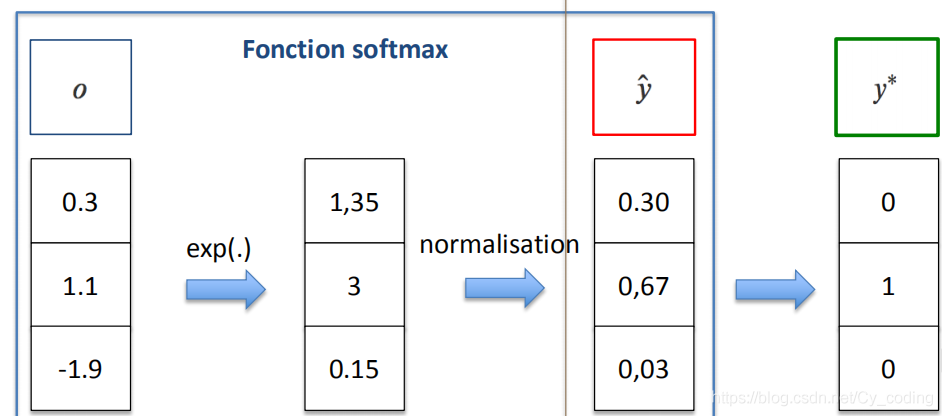
通過softmax函數構建概率分布再通過交叉熵,我們就構建了交叉熵損失函數。



















