MySQL為何不選擇平衡二叉樹

既然平衡二叉樹解決了普通二叉樹的問題，那么mysql為何不選擇平衡二叉樹作為索引呢?

索引需要存儲什么

讓我們想一想，如果我們要把索引存起來，那么應該存哪些信息呢，它應該存儲三塊信息：

• 索引的值：就是表里面索引列對應的值。

• 數據的磁盤地址(通過磁盤地址找到當前數據)或者直接存儲整條數據。

• 子節點的引用：我們需要從根節點往下走，所以需要知道左右子節點的地址。 根據這三點，可以有如下大致的一個簡單的結構圖：

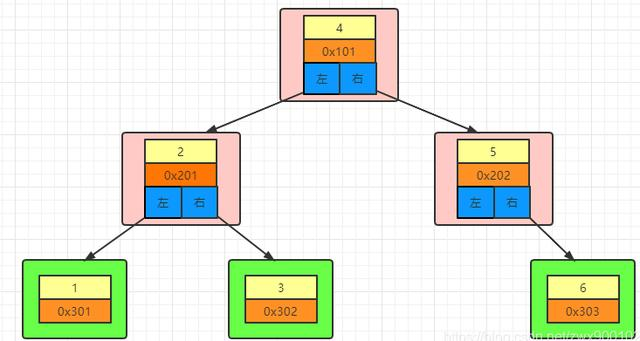
上圖中數字表示的是索引的值，0x開頭的表示磁盤地址，根節點中存了左右節點的引用。

AVL樹用來存儲索引存在什么問題

我們知道，頁（Page）是 Innodb 存儲引擎用于管理數據的最小磁盤單位，頁的默認大小為16KB。頁也就是上圖中的節點，每查詢一次節點就需要進行一次IO操作，IO操作是一種非常耗時的操作，很多業務系統的瓶頸都是卡在IO操作上，所以如果我們需要提高查詢效率的辦法之一就是減少IO次數，那么問題就來了，AVL樹一個節點上只存了一個關鍵字(索引值)+一個磁盤地址+左右節點的引用，這是遠遠達不到16KB的，會浪費了大量的空間。

上圖中如果我們要找到6這條數據，需要進行3次IO(獲取一個節點就是一個IO操作)，如果這棵樹很高的話，就會進行大量的IO操作，所以說AVL樹存在的最大問題就是空間利用不足，浪費了大量空間，數據量大的時候就會成為一顆瘦高的樹，那么我們可以怎么改進呢？答案很明顯了，那就是每個磁盤塊多存一點東西，也就是說每個磁盤多存幾個關鍵字，因為關鍵字越多，路數越多；路數越多，樹也就越矮越胖，相應的操作IO次數就會越少。

多路平衡樹(Balanced Tree)

多路平衡樹簡稱B樹，又稱B-樹，和AVL樹一樣，B樹在枝節點和葉子節點存儲鍵值、磁盤地址、左右節點引用。請看下圖的一個多路平衡樹的示例：

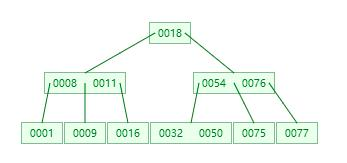
B樹的特點

相比較AVL樹，B樹一個磁盤上可以存多個關鍵字(值)，而且有一個特點就是：

• 分叉數（路數）永遠比關鍵字數多1。 我們可以畫出如下簡圖(下圖中只畫了3路，即兩個關鍵字，實際取決于一頁能存儲多少個關鍵字)：

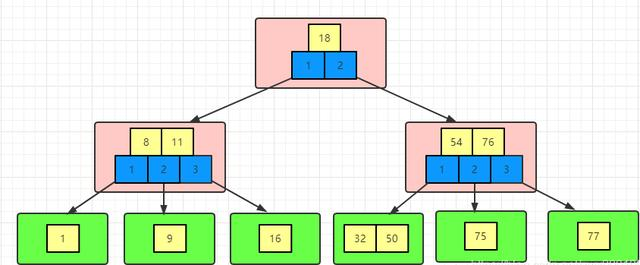
從上圖可以很明顯的看出，同樣高度的樹，B樹能存的數據遠遠大于平衡二叉樹。

B樹是如何查找數據的

以上圖為例，假如我們要找key=32這個數字，首先獲取到根節點，發現18小于key，所以往右邊走，獲取到右邊的數據，54和76，這時候遵循以下原則：

• key<54,命中最左邊分叉；

• key=54,直接命中，返回數據；

• 54<key<76,走中間的一個分叉；

• key=76,直接命中，返回數據；

• key>76，命中右邊分支； 這里因為key=32，所以走得是第1條，命中左邊分支，這時候再去獲取左邊分支，獲取到32和50，比較發現key=32，命中，返回數據。

從上面我們可以看出B樹效率相對于AVL樹，在數據量大的情況效率已經提高了很多，那么為什么MySQL還是不選擇B樹作為索引呢？ 那么接下來讓我們先看看改良版的B+樹，然后再下結論吧！

B+樹

B+樹由B樹改良而來，屬于改良版的多路平衡查找樹。 首先讓我們來看看B+樹到底長什么樣呢：

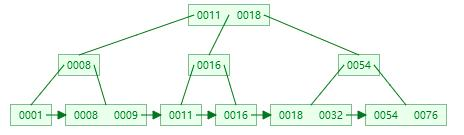
對比B+樹，我們可以發現一個很明顯的區別就是葉子節點有一個箭頭指引而且從左到右是有序的。

InnoDB中使用的B+樹相比較于傳統B+樹，改進之后的B+樹具有以下特點

InnoDB中B+樹的特點

• 它的關鍵字的數量是跟路數相等的。

• B+樹的根節點和枝節點中都不會存儲數據，只有葉子節點才存儲數據。而搜索到關鍵字不會直接返回，會到最后一層的葉子節點。

• B+樹的每個葉子節點增加了一個指向相鄰葉子節點的指針，它的最后一個數據會指向下一個葉子節點的第一個數據，形成了一個有序鏈表的結構。

• 它是根據左閉右開的區間來檢索數據的 按照B+樹的特點，我們可以畫出一個存儲數據的簡圖，如下：

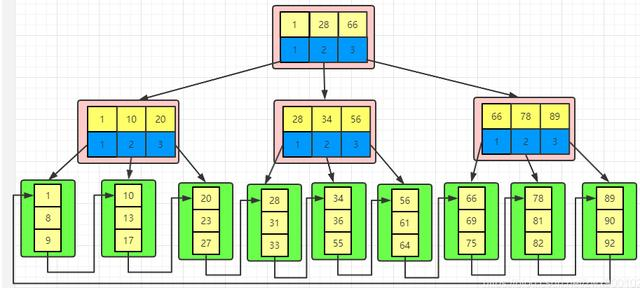
最后

給大家送上一份福利，領取方式：戳這里免費下載

Java架構進階面試及知識點文檔筆記

這份文檔共498頁，其中包括Java集合，并發編程，JVM，Dubbo,Redis，Spring全家桶，MySQL，Kafka等面試解析及知識點整理

Java分布式高級面試問題解析文檔

其中都是包括分布式的面試問題解析，內容有分布式消息隊列，Redis緩存，分庫分表，微服務架構，分布式高可用，讀寫分離等等！

互聯網Java程序員面試必備問題解析及文檔學習筆記

Java架構進階視頻解析合集

)]

互聯網Java程序員面試必備問題解析及文檔學習筆記

[外鏈圖片轉存中…(img-kDFntc1E-1625205424045)]

Java架構進階視頻解析合集