如何利用pytorch創建一個簡單的網絡模型？

Step1. 感知機，多層感知機（MLP）的基本結構

感知機（Perceptron）是神經網絡中的基本單元，神經網絡的雛形，也被稱作神經元（原理就是仿照生物上的神經元）、單層神經網絡。

通過設置不同的權重，并加上一個激活函數（判決門限），就構成了一個單層感知機的基本網絡結構，可以實現與或非三種基本邏輯：


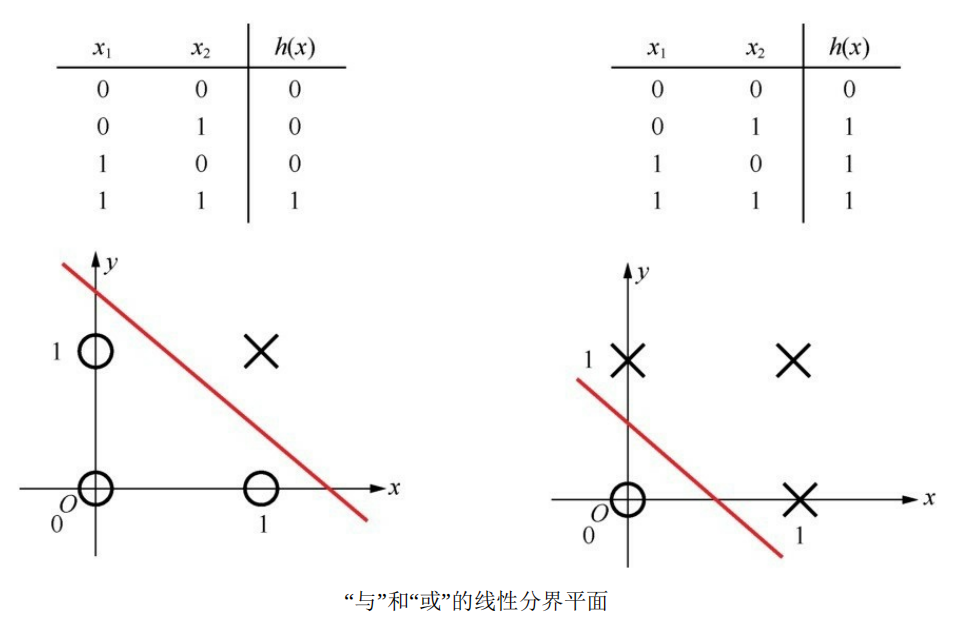
但是單層感知機的功能還是具有局限性，因為它畢竟只是一種二元線性分類模型（其輸入為實例的特征向量，輸出為實例的類別，取1和0【sigmoid激活判決】或+1和-1【sign激活判決】 ），像同或、異或這種稍微復雜一點的邏輯，就無法用單層感知機擬合出結果：

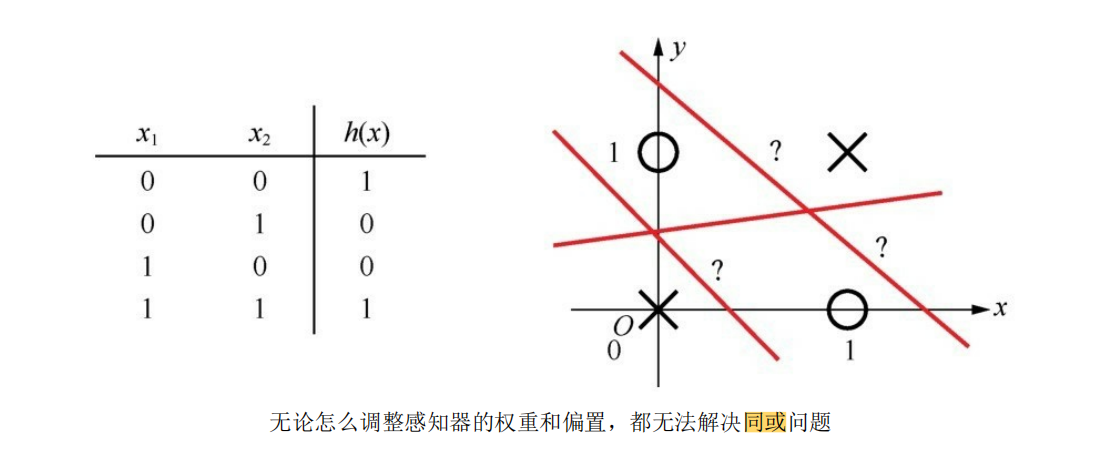
所以通過擴展感知機的層數，引入更多層的神經元（多層感知機MLP的由來），從而帶來更多可以訓練的參數，得到一種非線性模型，以達到擬合出預期的效果：

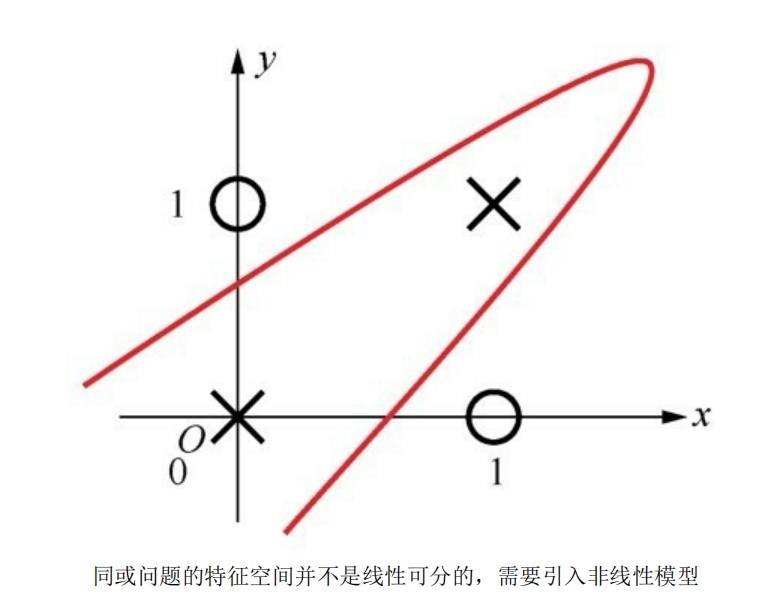
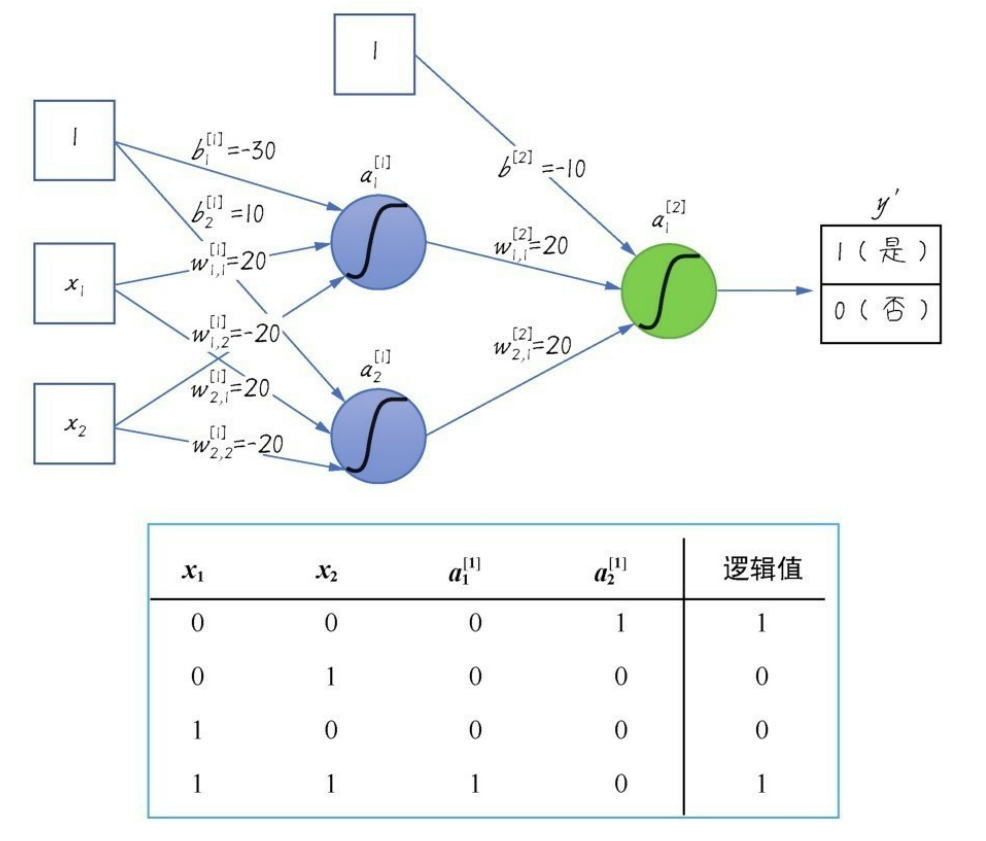
加入一層隱層網絡之后，同或數據集就變得可以擬合了：

$a_1^{[1]}=sigmoid({\omega }_{1,1}^{[1]}?x_1+{\omega }_{2,1}^{[1]}?x_2+b_1^{[1]})$

$a_2^{[1]}=sigmoid({\omega }_{2,1}^{[1]}?x_1+{\omega }_{2,2}^{[1]}?x_2+b_2^{[1]})$

$a_1^{[2]}=sigmoid({\omega }_{1,1}^{[2]}?a_1^{[1]}+{\omega }_{2,1}^{[2]}?a_2^{[1]}+b^{[2]})$【邏輯值】

上標${}^{[i]}$代表第幾層；

Step2. 超平面 ${\omega }^T?x+b=0$ or ${\omega }^T?x=b$

初學者第一次見到 ${\omega }^T?x+b=0$這個表達式時，會覺得它非常像線性函數， ${\omega }^T?x+b=0$為什么是一條斜線呢？實際上這只是為了在二維平面更好表示其線性分類效果；

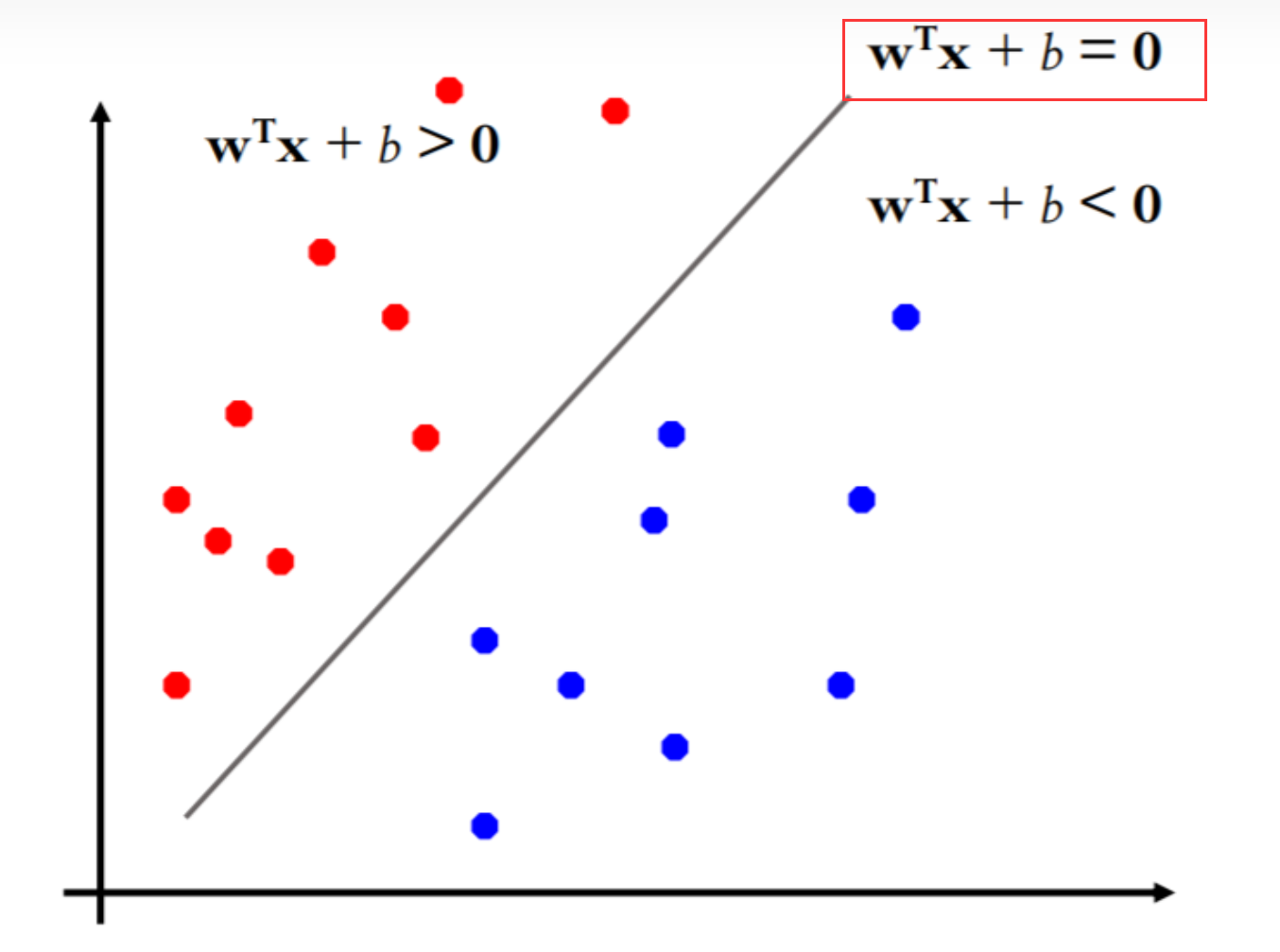
在三維空間中，分類效果是這樣：

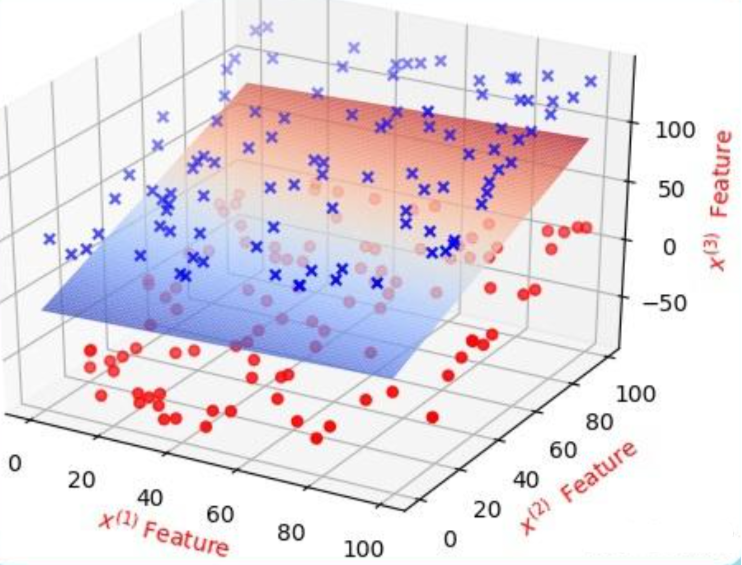
投影在 XOZ/YOZ 軸平面就是二維平面中所看到的效果。

在高等數學中我們學習過三維平面的一般表達式：$Ax+By+Cz+D=0$，

$(A,B,C)$為平面的法向量，亦可寫為點法式：$A(x?x_0)+B(y?y_0)+C(z?z_0)=0$，

$(x_0,y_0,z_0)$是平面上的一個點，將點法式拆開：$Ax+By+Cz=A{x}_0+B{y}_0+C{z}_0$，

這里的$A{x}_0+B{y}_0+C{z}_0$就是一般式中的$D$.

當擴展至N維超平面時，式子就變成了：$A(x_1?x_0)+B(x_2?x_0)+C(x_3?x_0)+...+N(x_n?x_0)=0$，

即$A{x}_1+B{x}_2+C{x}_3+...N{x}_n=A{x}_0+B{x}_0+C{x}_0+...N{x}_0$，

改寫成向量相乘的形式：

令行向量${\omega }^T=[{\omega }_1,{\omega }_2,...,{\omega }_n]=[A,B,...,N]$，

列向量$x=[x_1,x_2,...,x_n{]}^{\prime }$，$b=A{x}_0+B{x}_0+C{x}_0+...N{x}_0$

則N維超平面的定義式：${\omega }^T?x=b$ 就產生了，$b$為超平面的常數項截距，${\omega }^T$是超平面的法向量。

感知機函數

Step1中我們見過了感知機加激活函數得到與門的效果：

感知機函數可以表示為：$Sigmoid({\omega }^{T}x+b)$

$Sigmoid({\omega }^T?x+b)=\{\begin{array}{l}1,{\omega }^{T}x+b\ge 0\\ 0,{\omega }^{T}x+b<0\end{array}$

或

$Sign({\omega }^T?x+b)=\{\begin{array}{l}+1,{\omega }^{T}x+b\ge 0\\ ?1,{\omega }^{T}x+b<0\end{array}$

我們現在采用 $Sign$ 符號函數作為激活函數，利用超平面 ${\omega }^{T}x+b=0$ 進行決策分類任務，并定義輸出標簽 $y=+1$ 時為“是”，$y=?1$ 時為“否”；

則分類出現錯誤時必定會有$y?({\omega }^{T}x+b)<0$.

因此，我們定義損失函數：$\mathcal{L}(\omega ,b)=?{\sum }_{i=1}^n{y}_i?({\omega }_i^{T}x+b)$；

實際上損失函數的定義也并非這么直截了當就得出，因為還要保證損失函數連續可導，才能對其求偏導進行$argmin(\omega ,b)$;極小化損失函數的過程不是一次使得所有誤分類點的梯度下降，而是一次隨機選取一個誤分類點使其梯度下降，而損失函數中$y_i?({\omega }_i^{T}x+b)$的由來，其實就是選取了誤分類點到超平面距離公式中的分子項，分母項是個L2范數只起到了縮放作用，不影響損失函數的優化，所以可以忽略不計。
具體推導過程可以參考：感知機w·x+b=0怎么理解？數學推導是什么樣的？

我們的目標就是想讓損失函數盡可能地小，并選取使得損失函數最小的$w$和$b$.

利用經典的隨機梯度下降（SGD）算法對損失函數進行優化訓練：

$\{\begin{array}{l}\frac{?L}{?\omega }=\mathcal{L}(\omega ,b)=?{\sum }_{i=1}^n{y}_i?x\\ \frac{?L}{?b}=\mathcal{L}(\omega ,b)=?{\sum }_{i=1}^n{y}_i\end{array}$

$\{\begin{array}{l}\omega =\omega +\alpha \frac{?L}{?\omega }\\ b=b+\alpha \frac{?L}{?b}\end{array}$

利用感知機進行線性分類的訓練過程如上，這也是支持向量機（SVM）算法的雛形。

Step3. 利用感知機進行決策分類的訓練過程 -【Matlab代碼】

clc,clear,close all;
%% 定義變量
n = 50;        % 正負樣本的個數，總樣本數為2n
r = 0.5;       % 學習率
m = 2;         % 樣本的維數
i_max = 100;  % 最大迭代次數%% 生成樣本（以二維為例）
pix = linspace(-pi,pi,n);
randx = 2*pix.*rand(1,n) - pi;
x1 = [cos(randx) + 2*rand(1,n); 3+sin(randx) + 2*rand(1,n)];
x2 = [3+cos(randx) + 2*rand(1,n); sin(randx) + 2*rand(1,n)];
x = [x1'; x2'];  % 一共2n個點
y = [ones(n,1); -ones(n,1)];  %添加標簽
figure(1)
hold on; 
plot(x1(1,:),x1(2,:),'rx'); 
plot(x2(1,:),x2(2,:),'go'); %% 訓練感知機
x = [ones(2*n,1) x];    % 增加一個常數偏置項 [1, x1;x2]
w = zeros(1,m+1);       % 初始化權值 [w0, w1, w2]
flag = true;            % 退出循環的標志，為true時退出循環
for i=1:i_max for j=1:2*n if sign(x(j,:)*w') ~= y(j)  % 超平面加激活函數：sign(w'x+w0)disp(num2str(sign(x(j,:)*w')))disp(y(j))flag = false; w = w + r*y(j)*x(j,:);  % 利用SGD算法更新參數% beginpause(0.3);cla('reset');axis([-1,6,-1,6]);hold onplot(x1(1,:),x1(2,:),'rx'); plot(x2(1,:),x2(2,:),'go');x_test = linspace(0,5,20); y_test = -w(2)/w(3).*x_test-w(1)/w(3); plot(x_test,y_test,'m-.');% endM=getframe(gcf);nn=frame2im(M);[nn,cm]=rgb2ind(nn,256);if i==1imwrite(nn,cm,'out.gif','gif','LoopCount',inf,'DelayTime',0.1);elseimwrite(nn,cm,'out.gif','gif','WriteMode','append','DelayTime',0.5)endend end if flagdisp(num2str(sign(x(j,:)*w')))disp(y(j))break; end 
end
disp(num2str(sign(x(j,:)*w')))
disp(y(j))%% 畫分割線
cla('reset');
hold on
axis([-1,6,-1,6]);
plot(x1(1,:),x1(2,:),'rx'); 
plot(x2(1,:),x2(2,:),'go');
x_test = linspace(0,5,20); 
y_test = -w(2)/w(3).*x_test-w(1)/w(3);  
plot(x_test,y_test,'linewidth',2);
legend('標簽為正的樣本','標簽為負的樣本','分類超平面');
M=getframe(gcf);
nn=frame2im(M);
[nn,cm]=rgb2ind(nn,256);
imwrite(nn,cm,'out.gif','gif','WriteMode','append','DelayTime',0.5)

程序中的超平面就是一條二維直線：${\omega }_1+{\omega }_2{x}_1+{\omega }_3{x}_2=0$，

訓練出的超平面縱坐標 $y_{test}=x_2=?{\omega }_1/{\omega }_3?{\omega }_2{x}_1/{\omega }_3$.

打印觀察$Sign({\omega }^T?x+b)$和標簽$y$的值：

disp(num2str(sign(x(j,:)*w')))disp(y(j))

011-1-111-1-111-1-111-1-111-1-111-1-111-1-111-1-1-1

可以看到當$Sign({\omega }^T?x+b)==y$的時候終止迭代循環，得到正確分類結果。

從線性回歸到貫序模型

除了感知機，ML入門時我們還會使用線性回歸和邏輯回歸這類經典統計分析方法。線性回歸就是想要通過數據，訓練出一個符合數據變化規律的超平面（二維中的超平面就是一條直線，三維中的超平面是一個平面）進行未來數據的預測。
正是因為實際問題中的數據可能是復雜多變的，所以僅靠線性的超平面不一定能得到最好的擬合效果，所以可以通過添加其他的網絡結構，添加非線性的隱藏層來實現具有更復雜擬合能力的網絡結構。

而所謂的貫序模型就是將自定義的不同層網絡（可以是線性層，激活函數層，卷積層、池化層、循環層、注意力層等等）串成一個模型。

# 添加激活層后的貫序模型
seq_model = nn.Sequential(OrderedDict([('input_linear', nn.Linear(1, 12)),('hidden_activation', nn.Tanh()),('output_linear', nn.Linear(12, 1))
]))

該模型的網絡結構包括：
輸入層：第一層是一個線性層 (nn.Linear(1, 12))，它將接受一個維度為1的輸入。
隱藏層：包含一個激活函數層 (nn.Tanh())。該隱藏層不改變維度，僅應用激活函數。
輸出層：包含一個線性層 (nn.Linear(12, 1))，將隱藏層的輸出維度(12)投影到一個維度為1的輸出。
因此，該模型總共有三層：輸入層、隱藏層和輸出層。輸入層的維度為1，輸出層的維度為1。

nn.Linear(_, _)

nn.Linear 是 PyTorch 中的一個類，也可以理解為一個函數，用于定義一個線性變換（也稱為全連接層或仿射變換），將輸入特征映射到輸出特征。它是神經網絡模塊 nn 提供的一個常用函數之一。

nn.Linear(in_features, out_features)中的第一個參數為in_features: 輸入特征的數量（維度）。這個參數決定了輸入的大小，通常也就是數據集中的特征數，即輸入張量的最后一維大小；

nn.Linear(in_features, out_features)中的第二個參數為out_features: 輸出特征的數量（維度）。這個參數決定了輸出的大小，即輸出張量的最后一維大小。

bias: 是否在變換中使用偏置項（偏置向量）。默認為 True，表示會使用偏置項；設置為 False 則不使用偏置項。
前向傳播計算： 在神經網絡的前向傳播過程中，nn.Linear 定義的線性變換會對輸入特征進行矩陣乘積運算，然后加上偏置項。具體計算公式如下：

$\text{output}=\text{input}\times {\text{weight}}^{?}+\text{bias}$

其中，in_features是需要嚴格按照數據集中需要訓練的特征數確定的，如波士頓房價數據集中：

0-505就是數據集的batch_size，batch_size表示一次選多少行數據進行訓練，而crim, age, tax…這類的特征一共14個特征數量，就是nn.Linear中的in_features了，當然大小也是根據你需要哪幾個特征參與訓練確定的。

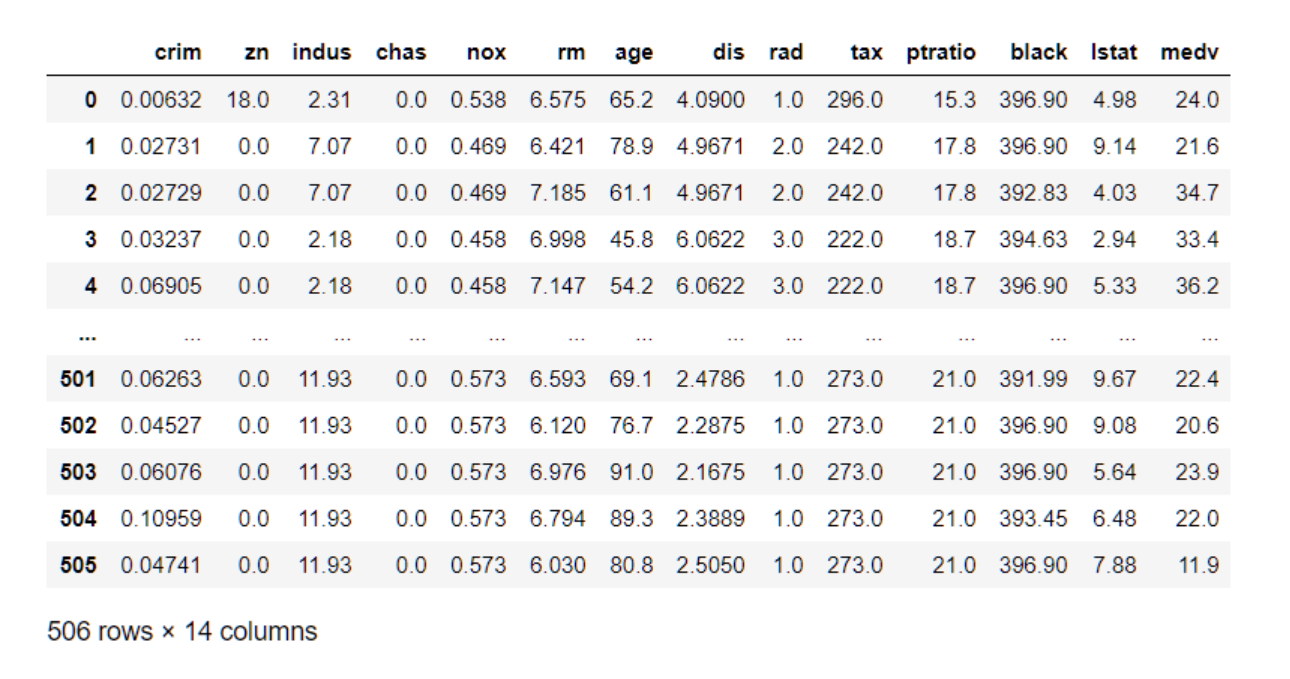
nn,Linear線性層計算的輸入和輸出格式：

相比in_features, out_features 就靈活多變一些。如果 out_features 設置得太大，模型可能會過于復雜，導致過擬合問題。相反，如果設置得太小，模型可能無法捕捉足夠的特征，導致欠擬合問題。選擇適當的輸出特征數量是在訓練集和驗證集上達到良好性能的關鍵之一。

nn.Linear 在神經網絡中非常常見，它可以用于構建模型的一層或多層，實現從輸入到輸出的特征變換。通過多層的堆疊和非線性激活函數的引入，可以構建出更復雜的神經網絡模型，適用于各種任務。

模型訓練

在pytorch中我們通過定義一個training_loop來指定模型訓練時的迭代次數，所選優化方法，調用創建的網絡模型，以及選取的損失函數、訓練集/驗證集：

def training_loop(n_epochs, optimizer, model, loss_fn, t_u_train, t_u_val,t_c_train, t_c_val):for epoch in range(1, n_epochs + 1):t_p_train = model(t_u_train)loss_train = loss_fn(t_p_train, t_c_train)t_p_val = model(t_u_val)loss_val = loss_fn(t_p_val, t_c_val)optimizer.zero_grad()   # 清除舊梯度loss_train.backward()   # 后向傳播計算新梯度optimizer.step()        # 根據梯度進行SGD優化if epoch == 1 or epoch % 500 == 0:print(f"Epoch {epoch}, Training loss {loss_train.item():.4f},"f" Validation loss {loss_val.item():.4f}")def loss_fn(t_p, t_c):squared_diffs = (t_p - t_c) ** 2return squared_diffs.mean()linear_model = nn.Linear(1, 1)
optimizer = optim.SGD(linear_model.parameters(), lr=1e-2)# 嘗試線性模型訓練
training_loop(n_epochs=3000,optimizer=optimizer,model=linear_model,# loss_fn=loss_fn,loss_fn=nn.MSELoss(),t_u_train=t_un_train,t_u_val=t_un_val,t_c_train=t_c_train,t_c_val=t_c_val)

貫序模型例程 -【Pytorch完整代碼】

import torch
import torch.optim as optim
import torch.nn as nn
from collections import OrderedDict
from matplotlib import pyplot as plttorch.set_printoptions(edgeitems=2, linewidth=75)# 數據集準備
t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_c = torch.tensor(t_c).unsqueeze(1)
t_u = torch.tensor(t_u).unsqueeze(1)n_samples = t_u.shape[0]  # 獲取數據集的樣本數量（數據集中元素的數量）
n_val = int(0.2 * n_samples)  # 計算驗證集的樣本數量。這里使用了0.2作為驗證集的比例，將數據集中的20%作為驗證集# 生成一個長度為n_samples的隨機排列的索引數組。這里使用torch.rand-perm函數生成一個隨機排列的整數數組，用于打亂原始數據集的索引順序
shuffled_indices = torch.randperm(n_samples)
train_indices = shuffled_indices[:-n_val]
val_indices = shuffled_indices[-n_val:]
t_u_train = t_u[train_indices]
t_c_train = t_c[train_indices]
t_u_val = t_u[val_indices]
t_c_val = t_c[val_indices]
t_un_train = 0.1 * t_u_train
t_un_val = 0.1 * t_u_vallinear_model = nn.Linear(1, 1)
linear_model(t_un_val)def training_loop(n_epochs, optimizer, model, loss_fn, t_u_train, t_u_val,t_c_train, t_c_val):for epoch in range(1, n_epochs + 1):t_p_train = model(t_u_train)loss_train = loss_fn(t_p_train, t_c_train)t_p_val = model(t_u_val)loss_val = loss_fn(t_p_val, t_c_val)optimizer.zero_grad()   # 清除舊梯度loss_train.backward()   # 后向傳播計算新梯度optimizer.step()        # 根據梯度進行SGD優化if epoch == 1 or epoch % 500 == 0:print(f"Epoch {epoch}, Training loss {loss_train.item():.4f},"f" Validation loss {loss_val.item():.4f}")def loss_fn(t_p, t_c):squared_diffs = (t_p - t_c) ** 2return squared_diffs.mean()linear_model = nn.Linear(1, 1)
optimizer = optim.SGD(linear_model.parameters(), lr=1e-2)# 嘗試線性模型訓練
training_loop(n_epochs=3000,optimizer=optimizer,model=linear_model,# loss_fn=loss_fn,loss_fn=nn.MSELoss(),t_u_train=t_un_train,t_u_val=t_un_val,t_c_train=t_c_train,t_c_val=t_c_val)print()
print(linear_model.weight)
print(linear_model.bias)# 添加激活層后的貫序模型
seq_model = nn.Sequential(OrderedDict([('input_linear', nn.Linear(1, 12)),('hidden_activation', nn.Tanh()),('output_linear', nn.Linear(12, 1))
]))print(seq_model)
print([param.shape for param in seq_model.parameters()])for name, param in seq_model.named_parameters():print(name, param.shape)optimizer = optim.SGD(seq_model.parameters(), lr=1e-3)training_loop(n_epochs=5000,optimizer=optimizer,model=seq_model,        # 使用貫序模型重新訓練loss_fn=nn.MSELoss(),t_u_train=t_un_train,t_u_val=t_un_val,t_c_train=t_c_train,t_c_val=t_c_val)# 打印模型參數訓練結果：
# print('output', seq_model(t_un_val))
# print('answer', t_c_val)
# print('hidden', seq_model.hidden_linear.weight.grad)t_range = torch.arange(20., 90.).unsqueeze(1)fig = plt.figure(dpi=100)
plt.xlabel("Fahrenheit")
plt.ylabel("Celsius")
plt.plot(t_u.numpy(), t_c.numpy(), 'o')
plt.plot(t_range.numpy(), seq_model(0.1 * t_range).detach().numpy(), 'c-')
plt.plot(t_u.numpy(), seq_model(0.1 * t_u).detach().numpy(), 'kx')
plt.show()

打印結果：

Epoch 1, Training loss 287.7947, Validation loss 243.3686
Epoch 500, Training loss 6.3782, Validation loss 5.3946
Epoch 1000, Training loss 2.9283, Validation loss 6.1271
Epoch 1500, Training loss 2.4918, Validation loss 6.4090
Epoch 2000, Training loss 2.4366, Validation loss 6.5120
Epoch 2500, Training loss 2.4296, Validation loss 6.5489
Epoch 3000, Training loss 2.4288, Validation loss 6.5621Parameter containing:
tensor([[5.4817]], requires_grad=True)
Parameter containing:
tensor([-17.4273], requires_grad=True)
Sequential((hidden_linear): Linear(in_features=1, out_features=12, bias=True)(hidden_activation): Tanh()(output_linear): Linear(in_features=12, out_features=1, bias=True)
)
[torch.Size([12, 1]), torch.Size([12]), torch.Size([1, 12]), torch.Size([1])]
hidden_linear.weight torch.Size([12, 1])
hidden_linear.bias torch.Size([12])
output_linear.weight torch.Size([1, 12])
output_linear.bias torch.Size([1])
Epoch 1, Training loss 200.8066, Validation loss 149.6482
Epoch 500, Training loss 8.0419, Validation loss 6.9692
Epoch 1000, Training loss 2.8967, Validation loss 9.0610
Epoch 1500, Training loss 1.7860, Validation loss 8.2857
Epoch 2000, Training loss 1.4266, Validation loss 7.6947
Epoch 2500, Training loss 1.3101, Validation loss 7.3714
Epoch 3000, Training loss 1.2710, Validation loss 7.2340
Epoch 3500, Training loss 1.2550, Validation loss 7.2035
Epoch 4000, Training loss 1.2451, Validation loss 7.2175
Epoch 4500, Training loss 1.2367, Validation loss 7.2404
Epoch 5000, Training loss 1.2289, Validation loss 7.2637

這個例子中雖然采用的輸入層和輸出層都是線性層nn.Linear，但是最終擬合出的卻是曲線，而非二維的超平面（一條直線），這就是因為隱藏層我們選用了tanh函數，是非線性的，也因此提升了網絡的擬合效果：

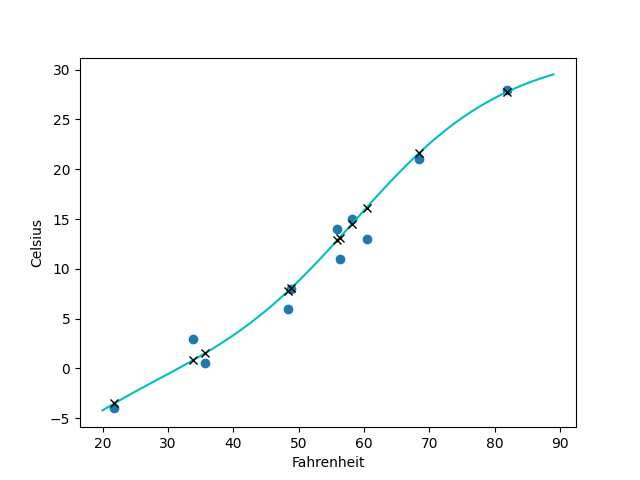
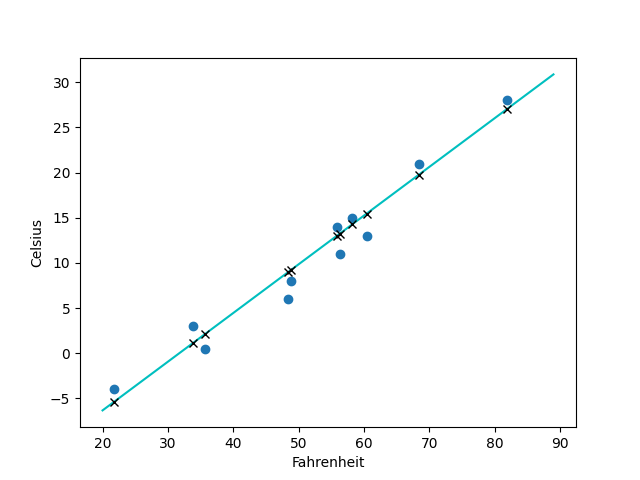
如果我們將nn.Tanh()改為nn.Relu()激活函數，擬合出來的就是一條直線了：

參考文獻：
[1] Pytorch官方 - Deep Learning With Pytorch
[2] 《零基礎學機器學習》
[3] 感知機 - 謝晉- 算法與數學之美
[4] 感知機w·x+b=0怎么理解？數學推導是什么樣的？
[5] 啥都斷更的小c-從0開始深度學習：什么是線性層？pytorch中nn.linear怎么用？
[6] 機器學習| 算法筆記-線性回歸（Linear Regression）