核心問題就是那個等式
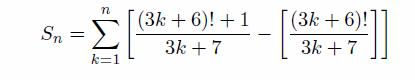
我們觀察到等式可以寫成(n-1)!-1/n-[(n-1)!/n]的形式，這樣就應該聯想到威爾遜定理了。
回顧一下威爾遜定理的內容：當且僅當n為素數的時候n|(n-1)!-1，n為合數且大于4的時候n|(n-1)!【參見威爾遜定理的證明】
對于這個等式，n顯然是大于4的，那么如果n是一個合數，后一個就是一個整數，前一個就是這個整數加上一個1/n，向下取整以后就是0，如果n是一個素數，前一個為一個整數，后一個顯然不可能為整數，比前一個小1/n，那么向下取整以后差為1
因此Sn的變化規律就是，如果是質數就加1，如果是合數加0
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<iostream>
#include<cmath>
#include<ctime>
#include<climits>
#include<queue>
#include<vector>
#include<set>
#include<map>
using namespace std;typedef long long ll;
const int INF=0x3f3f3f3f;
const int MAXN=3e6+50;
int prime[MAXN];
bool check[MAXN];
int ans[MAXN];
int tot=0;void creat_prime()
{for(int i=2;i<MAXN;i++){if(!check[i]) prime[tot++]=i;for(int j=0;j<tot && prime[j]*i<MAXN;j++){check[prime[j]*i]=true;if(i%prime[j]==0) break;}}
}void init()
{int limit=1e6+5;for(int i=1;i<limit;i++){if(!check[3*i+7]) ans[i]=ans[i-1]+1;else ans[i]=ans[i-1];}
}int main()
{creat_prime();init();int T,n;scanf("%d",&T);while(T--){scanf("%d",&n);printf("%d\n",ans[n]);}return 0;
}
)
)
