轉載請注明出處：http://blog.csdn.net/ns_code/article/details/20227303

前言

? ??堆排序、快速排序、歸并排序（下篇會寫這兩種排序算法）的平均時間復雜度都為O（n*logn）。要弄清楚堆排序，就要先了解下二叉堆這種數據結構。本文不打算完全講述二叉堆的所有操作，而是著重講述堆排序中要用到的操作。比如我們建堆的時候可以采用堆的插入操作（將元素插入到適當的位置，使新的序列仍符合堆的定義）將元素一個一個地插入到堆中，但其實我們完全沒必要這么做，我們有執行操作更少的方法，后面你會看到，我們基本上只用到了堆的刪除操作，更具體地說，應該是刪除堆的根節點后，將剩余元素繼續調整為堆的操作。先來看二叉堆的定義。

二叉堆

? ? 二叉堆其實是一棵有著特殊性質的完全二叉樹，這里的特殊性質是指：

? ? 1、二叉堆的父節點的值總是大于等于（或小于等于）其左右孩子的值；

? ? 2、每個節點的左右子樹都是一棵這樣的二叉堆。

? ? 如果一個二叉堆的父節點的值總是大于其左右孩子的值，那么該二叉堆為最大堆，反之為最小堆。我們在排序時，如果要排序后的順序為從小到大，則需選擇最大堆，反之，選擇最小堆，這點通過后面對堆排序分析，你會有所體會。

堆排序

? ? 由二叉堆的定義可知，堆頂元素（即二叉堆的根節點）一定為堆中的最大值或最小值，因此如果我們輸出堆頂元素后，將剩余的元素再調整為二叉堆，繼而再次輸出堆頂元素，再將剩余的元素調整為二叉堆，反復執行該過程，這樣便可輸出一個有序序列，這個過程我們就叫做堆排序。

? ? 由于我們的輸入是一個無序序列，因此要實現堆排序，我們要先后解決如下兩個問題：

? ? 1、如何將一個無序序列建成一個二叉堆；

? ? 2、在去掉堆頂元素后，如何將剩余的元素調整為一個二叉堆。

? ? 針對第一個問題，可能很明顯會想到用堆的插入操作，一個一個地插入元素，每次插入后調整元素的位置，使新的序列依然為二叉堆。這種操作一般是自底向上的調整操作，即先將待插入元素放在二叉堆后面，而后逐漸向上將其與父節點比較，進而調整位置。但正如前言中所說，我們完全用不著一個節點一個節點地插入，那我們要怎么做呢？我們需要先來解決第二個問題，解決了第二個問題，第一個問題問題也就迎刃而解了。

? ??調整二叉堆

? ? 要分析第二個問題，我們先給出以下前提：

? ? 1、我們排序的目標是從小到大，因此我們用最大堆；

? ? 2、我們將二叉堆中的元素以層序遍歷后的順序保存在一維數組中，根節點在數組中的位置序號為0。

? ? 這樣，如果某個節點在數組中的位置序號為i，那么它的左右孩子的位置序號分別為2i+1和2i+2。

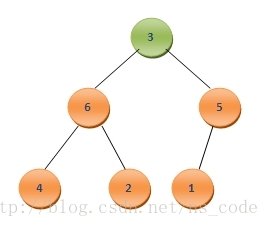
? ? 為了使調整過程更易于理解，我們采用如下二叉堆來分析（注意下面的分析，我們并沒有采用額外的數組來存儲每次去掉的堆頂數據）：?

??? ? ??

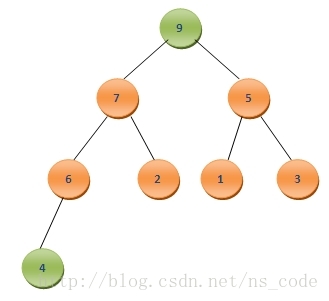
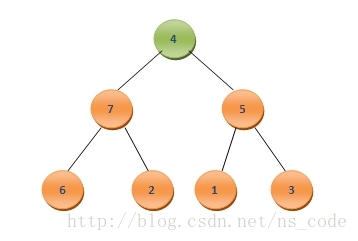
? ? 這里數組A中元素的個數為8，很明顯最大值為A0，為了實現排序后的元素按照從小到大的順序排列，我們可以將二叉堆中的最后一個元素A7與A0互換，這樣A7中保存的就是數組中的最大值，而此時該二叉樹變為了如下情況：

? ?

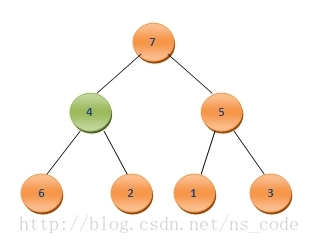
? ? 為了將其調整為二叉堆，我們需要尋找4應該插入的位置。為此，我們讓4與它的孩子節點中最大的那個，也就是其左孩子7，進行比較，由于4<7,我們便把二者互換，這樣二叉樹便變成了如下的形式：

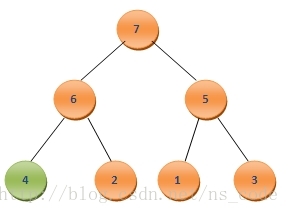
? ? 接下來，繼續讓4與其左右孩子中的最大者，也就是6，進行比較，同樣由于4<6，需要將二者互換，這樣二叉樹變成了如下的形式：

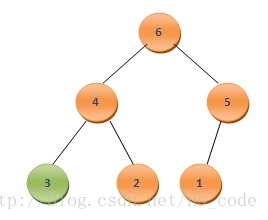
? ? 這樣便又構成了二叉堆，這時候A0為7，是所有元素中的最大元素。同樣我們此時繼續將二叉堆中的最后一個元素A6和A0互換，這樣A6中保存的就是第二大的數值7，而A0就變為了3，形式如下：

? ? 為了將其調整為二叉堆，一樣將3與其孩子結點中的最大值比較，由于3<6，需要將二者互換，而后繼續和其孩子節點比較，需要將3和4互換，最終再次調整好的二叉堆形式如下：

? ? 一樣將A0與此時堆中的最后一個元素A5互換，這樣A5中保存的便是第三大的數值，再次調整剩余的節點，如此反復，直到最后堆中僅剩一個元素，這時整個數組便已經按照從小到大的順序排列好了。

? ? 據此，我們不難得出將剩余元素繼續調整為二叉堆的操作實現代碼如下（同前面兩篇博文中一樣，我們不需每次比較后都交換元素位置，代碼中可以再次體會到這點）：

? ? 這樣，將已經建好的二叉堆進行排序的代碼如下：

? ??建立二叉堆

? ? 搞懂了第二個問題，那么我們回過頭來看如何將無序的數組建成一個二叉堆。

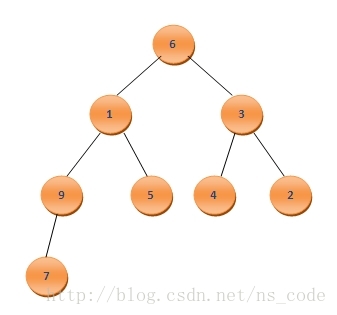
? ? 我們同樣以上面的數組為例，假設其數組內元素的原始順序為：A[]={6,1,3,9,5,4,2,7}，那么在沒有建成二叉堆前，個元素在該完全二叉樹中的存放位置如下：

? ? 這里的后面四個元素均為葉子節點，很明顯，這四個葉子可以認為是一個堆（因為堆的定義中并沒有對左右孩子間的關系有任何要求，所以可以將這幾個葉子節點看做是一個堆），而后我們便考慮將第一個非葉子節點9插入到這個堆中，再次構成一個堆，接著再將3插入到新的堆中，再次構成新堆，如此繼續，直到該二叉樹的根節點6也插入到了該堆中，此時構成的堆便是由該數組建成的二叉堆。因此，我們這里同樣可以利用到上面所寫的HeapAdjustDown(int *,int,int)函數，因此建堆的代碼可寫成如下的形式:

? ? 如果還不是很明白，注意讀下HeapAdjustDown(int *,int,int)函數代碼中關于該函數作用的注釋。

完整源碼

? ? 最后貼出完整源碼：

? ? 測試結果如下：

總結

? ? 最后我們簡要分析下堆排序的時間復雜度。我們在每次重新調整堆時，都要將父節點與孩子節點比較，這樣，每次重新調整堆的時間復雜度變為O（logn），而堆排序時有n-1次重新調整堆的操作，建堆時有（（len-1）/2+1）次重新調整堆的操作，因此堆排序的平均時間復雜度為O（n*logn）。由于我們這里沒有借用輔助存儲空間，因此空間復雜度為O（1）。

? ? 堆排序在排序元素較少時有點大才小用，待排序列元素較多時，堆排序還是很有效的。另外，堆排序在最壞情況下，時間復雜度也為O（n*logn）。相對于快速排序（平均時間復雜度為O（n*logn），最壞情況下為O（n*n）），這是堆排序的最大優點。