已知一系列除數和模數,求最小的滿足條件的數

我們先考慮一般的情況，即模數不互質。（擴展中國剩余定理）

我們考慮兩個方程的情況
x%M=R $x=k1?M+R$
x%m=r $x=k2?m+r$
所以$k1?M+R=k2?m+r$
即$k1?M?k2?m=r?R$
我們可以用擴展歐幾里得求出k1,求出一個x
X的解系為$X=x+k?lcm(M,m)$
即將原來的兩個方程變成了一個方程X%lcm(M,m)=x

剩下要做的就是不斷將方程進行合并合并成一個,再按要求輸出

由以上得到算法

bool mod_equation(ll n,ll &M,ll &R)
{ll m,r;scanf("%lld%lld",&M,&R);bool flag=true;for(int i=1;i<n;i++){scanf("%lld%lld",&m,&r);if(flag){ll k1,k2,C=r-R,d;ex_gcd(M,m,d,k1,k2);if(C%d)	{flag=false; continue;}k1=C/d*k1%(m/d); R+=k1*M; M=M/d*m; R%=M;}}R=(R%M+M)%M;return flag;
}

一個小問題是ax+by=gcd(a,b)的解系為x+b/d * k,y-a/d * k
而ax+by=c的一個解為x*=c/d y*=c/d,解系仍然為x+b/d * k,y-a/d * k,也就是說解系只和系數有關系而和等式右邊沒有關系

當模數互質的時候，我們不必要這樣做，可以直接構造出答案。

假設模數分別為m1,m2,…,mk，且(m1,m2,…,mk)=1,我們令M=lcm(m1,m2,…,mk)，ti為M/mi模mi的逆元，那么有一個答案為

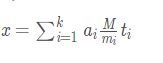
所有的答案為X=x+k*M

直覺上理解的話，x中M/mj模mi肯定是0，只有M/mi這項為ai

因此直接計算答案，逆元用擴展歐幾里得求解

bool mod_equation(ll n,ll &M,ll&R)
{M=1; ll t,d,k,x=0;for(int i=1;i<=n;i++) M=M*m[i];for(int i=1;i<=n;i++){ex_gcd(M/m[i],m[i],d,t,k);t=(t%m[i]+m[i])%m[i];x=(x+t*M/m[i]*r[i])%M;}R=(x%M+M)%M;return true;
}