紅黑樹概念及其相關操作的實現

紅黑樹的概念

紅黑樹，是一種二叉搜索樹，但它并不像AVL樹一樣，每個結點綁定一個平衡因子。但在每個結點上增加一個存儲位表示結點的顏色，可以是Red或Black。通過 對任何一條從根到葉子的路徑上各個結點著色方式的限制，紅黑樹確保沒有一條路徑會比其他路徑長出倆倍，因而是接近平衡的。
最長路徑中結點的個數不會超過最短路徑中結點個數的兩倍

紅黑樹的性質

每個結點不是紅色就是黑色
根節點是黑色的，空樹也是紅黑樹。
如果一個節點是紅色的，則它的兩個孩子結點是黑色的，不可能出現連在一起的紅色結點。
對于每個結點，從該結點到其所有后代葉結點的簡單路徑上,均包含相同數目的黑色結點，每條路徑里黑色結點個數是相等的。
每個葉子結點都是黑色的(此處的葉子結點指的是空結點)

問題

為什么滿足上面的性質，紅黑樹就能保證：其最長路徑中節點個數不會超過最短路徑節點個數的兩倍？
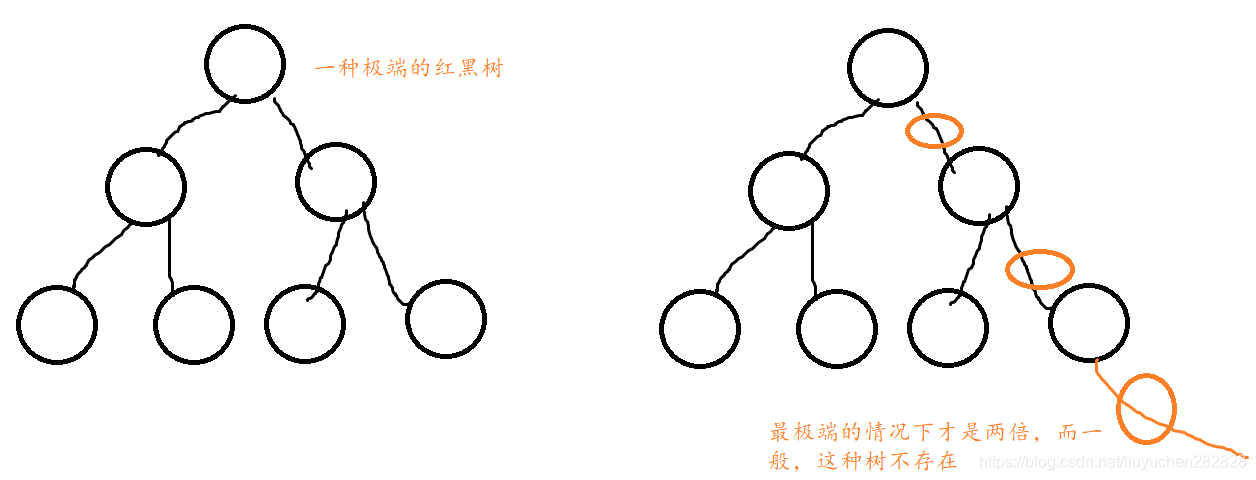
在這里插入圖片描述
極端情況下，剛好是兩倍，但是這種極端情況不存在。因為根結點是黑的，那么第二層的兩個結點都必須是紅色的。

紅黑樹的結構

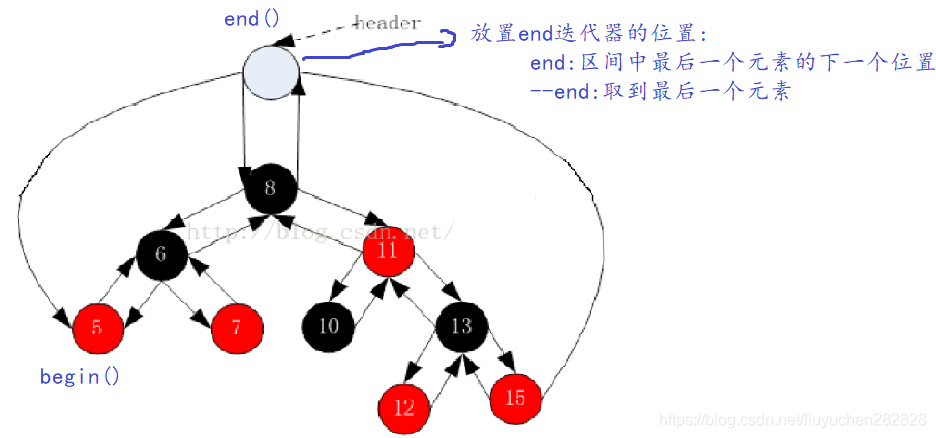
在這里插入圖片描述

紅黑樹結點的定義

enum COLOR{RED,BLACK};template<class T>
struct RBTreeNode
{RBTreeNode(const T& data = T(), COLOR color = RED):_pLeft(nullptr), _pRight(nullptr), _pParent(nullptr), _data(data), _color(color)	{}RBTreeNode<T>* _pLeft;RBTreeNode<T>* _pRight;RBTreeNode<T>* _pParent;T _data;COLOR _color;
};

為什么要將結點的默認顏色給成紅色的？

因為如果默認顏色是黑色的話，往已經是一顆紅黑樹里插入的話，性質4一定遭到破壞，所以給成紅色，有些情況下破壞，有些情況下不被破壞。

紅黑樹的插入

紅黑樹是在二叉搜索樹的基礎上加上其平衡限制條件，因此紅黑樹的插入可分為兩步：

1. 按照二叉搜索的樹規則插入新節點

template<class T>
class RBTree
{typedef RBTreeNode<T> Node;
public:RBTree(){_pHead = new Node;_pHead->_pLeft = _pHead;_pHead->_pRight = _pHead;//構造里已經將雙親給成空}bool Insert(const T&data){Node* pRoot = GetRoot();if (nullptr == pRoot) //樹為空,創建根結點{pRoot = new Node(data,BLACK);pRoot->_pParent = _pHead;//只有一個結點，head就是根節點的雙親_pHead->_pLeft = pRoot; //改變左右指針域_pHead->_pRight = pRoot;return true;}else{//說明樹已經不為空了//1.按照二叉搜索樹的性質找到帶插入結點在紅黑樹的位置Node* pCur = pRoot;Node* pParent = nullptr;while (pCur){pParent = pCur;//標記雙親位置if (data < pCur->_data)pCur = pCur->_pLeft;else if (data>pCur->_data)pCur = pCur->_pRight;else//相同不插入return false;}//2. 插入新結點pCur = new Node(data);if (data < pParent->_data)pParent->_pLeft = pCur;else{pParent->_pRight = pCur;}//3. 更新雙親位置pCur->_pParent = pParent;//4.檢測:是否新結點插入后連在一起的紅色結點if (RED == pParent->_color){//調整//檢測新節點插入后，紅黑樹的性質是否造到破壞}}//5.調整頭結點的左右指針域//保證根節點是黑色pRoot->_color = BLACK;_pHead->_pLeft=leftMost();_pHead->_pRight = RightMost();return true;}Node* LeftMost(){//得到根節點Node* pRoot = GetRoot();if (nullptr == pRoot)return _pHead;Node* pCur = pRoot;//找到最左側結點while (pCur->_pLeft)pCur = pCur->_pLeft;return pCur;}Node* RightMost(){//得到根節點Node* pRoot = GetRoot();if (nullptr == pRoot)return _pHead;Node* pCur = pRoot;//找到最右側結點while (pCur->_pRight)pCur = pCur->_pRight;return pCur;}
protected:Node*& GetRoot()  //head是new出來的，head存在parent一定存在，按引用方式返回沒有問題{//得到根節點，也就是頭結點的下一個結點return _pHead->_pParent;}
private:Node* _pHead;
};

2. 檢測新節點插入后，紅黑樹的性質是否造到破壞

因為新節點的默認顏色是紅色，因此：如果其雙親節點的顏色是黑色，沒有違反紅黑樹任何性質，則不需要調整；但當新插入節點的雙親節點顏色為紅色時，就違反了性質三不能有連在一起的紅色節點此時需要對紅黑樹分情況來討論
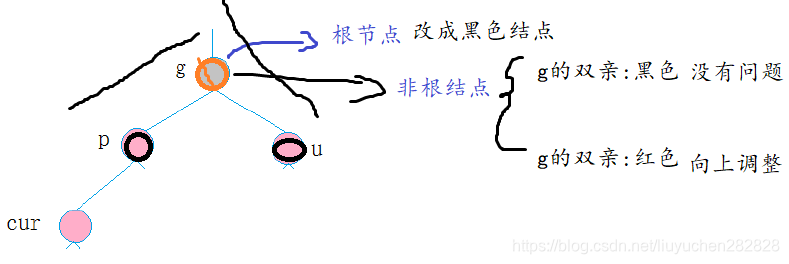
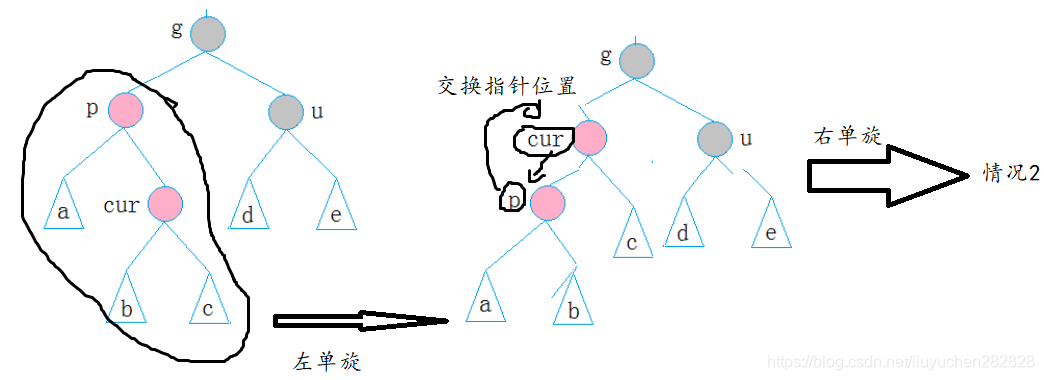
cur為當前節點，p為父節點，g為祖父節點，u為叔叔節點

2.1 cur為紅，p為紅，g為黑，u存在且為紅

解決方式：將p,u改為黑，g改為紅，然后把g當成cur，繼續向上調整。
在這里插入圖片描述

2.2 cur為紅，p為紅，g為黑，u不存在/u為黑

p為g的左孩子，cur為p的左孩子，則進行右單旋轉；相反，
p為g的右孩子，cur為p的右孩子，則進行左單旋轉
p、g變色–p變黑，g變紅
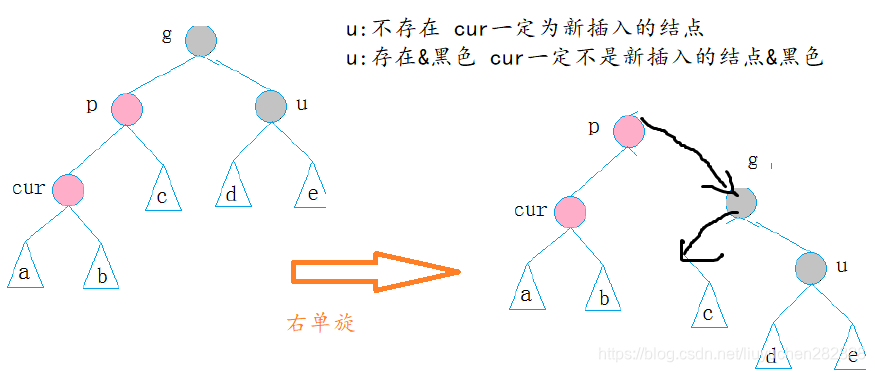
在這里插入圖片描述

如果u不存在，假設cur本來就存在，cur和雙親比然是黑的，因為兩個紅的不能連在一起，那么這條路徑里就有兩個黑色，所以不滿足性質4，cur所以一定是新插入的結點
如果u存在且為黑色，右側路徑里有兩個黑色路徑，因為兩條路徑黑色結點必須一樣。新節點一插入，插入到cur的子樹中，導致子樹中不滿足情況。向上調整時，把cur改成黑色。

2.3 cur為紅，p為紅，g為黑，u不存在/u為黑

在這里插入圖片描述

紅黑樹的驗證

紅黑樹的檢測分為兩步：

檢測其是否滿足二叉搜索樹(中序遍歷是否為有序序列)
檢測其是否滿足紅黑樹的性質

template<class T>
class RBTree
{typedef RBTreeNode<T> Node;
public:RBTree(){_pHead = new Node;_pHead->_pLeft = _pHead;_pHead->_pRight = _pHead;//構造里已經將雙親給成空}bool Insert(const T&data){Node*& pRoot = GetRoot(); //必須以引用的方式進行接受if (nullptr == pRoot) //樹為空,創建根結點{pRoot = new Node(data,BLACK);pRoot->_pParent = _pHead;//只有一個結點，head就是根節點的雙親_pHead->_pLeft = pRoot; //改變左右指針域_pHead->_pRight = pRoot;return true;}else{//說明樹已經不為空了//1.按照二叉搜索樹的性質找到帶插入結點在紅黑樹的位置Node* pCur = pRoot;Node* pParent = nullptr;while (pCur){pParent = pCur;//標記雙親位置if (data < pCur->_data)pCur = pCur->_pLeft;else if (data > pCur->_data)pCur = pCur->_pRight;else//相同不插入return false;}//2. 插入新結點pCur = new Node(data);if (data < pParent->_data)pParent->_pLeft = pCur;elsepParent->_pRight = pCur;//3. 更新雙親位置pCur->_pParent = pParent;//以上沒錯//4.檢測:是否新結點插入后連在一起的紅色結點while (pParent!=_pHead && RED == pParent->_color){Node* granderFather = pParent->_pParent;if (pParent == granderFather->_pLeft){//叔叔結點在右側Node* uncle = granderFather->_pRight;//情況一:叔叔結點存在，且為紅if (uncle && RED == uncle->_color){pParent->_color = BLACK;uncle->_color = BLACK;granderFather->_color = RED;pCur = granderFather;pParent = pCur->_pParent;}//以上沒問題else{//情況三if (pCur == pParent->_pRight) //情況三{//轉變成情況二RotateLeft(pParent);swap(pParent, pCur);}//情況二pParent->_color = BLACK;granderFather->_color = RED;RotateRight(granderFather);}//以上沒問題}else{//叔叔結點在左側Node* uncle = granderFather->_pLeft;//情況一的反情況if (uncle && uncle->_color == RED){pParent->_color = BLACK;uncle->_color = BLACK;granderFather->_color = RED;pCur = granderFather;pParent = pCur->_pParent;}//以上沒問題else{//情況三的反情況if (pCur == pParent->_pLeft)	/**/{//情況三的反情況變成情況二的反情況RotateRight(pParent);swap(pParent, pCur);}//情況二反情況處理pParent->_color = BLACK;granderFather->_color = RED;RotateLeft(granderFather);}//以上沒問題}}}//5.調整頭結點的左右指針域//保證根節點是黑色pRoot->_color = BLACK;_pHead->_pLeft = LeftMost();_pHead->_pRight = RightMost();return true;}void InOrder(){_InOrder(GetRoot());}//檢測紅黑樹bool IsValidRBTree(){Node* pRoot = GetRoot();if (nullptr == pRoot)return true;if (pRoot->_color != BLACK){cout << "違反性質2：根結點顏色必須為黑色" << endl;return false;}//獲取一條路徑中結點的個數size_t blackCount = 0; //基準值Node* pCur = pRoot;while (pCur){if (pCur->_color == BLACK)blackCount++;pCur = pCur->_pLeft;}size_t pathBlack = 0; //每條路徑中的黑色結點個數return _IsValidRBTree(pRoot, blackCount,pathBlack);}
protected:bool _IsValidRBTree(Node* pRoot, size_t blackCount, size_t pathBlack){if (nullptr == pRoot)return true;if (pRoot->_color == BLACK)pathBlack++;//檢測性質3Node* pParent = pRoot->_pParent;if (pParent != _pHead && pParent->_color == RED&&pRoot->_color == RED){cout << "違反性質3:不能有連在一起的紅色結點" << endl;return false;}if (nullptr == pRoot->_pLeft&&nullptr == pRoot->_pRight){//一條路徑到葉子if (blackCount != pathBlack){cout << "違反了性質4：每條路徑中黑色結點個數必須相同" << endl;return false;}}return _IsValidRBTree(pRoot->_pLeft, blackCount, pathBlack) &&_IsValidRBTree(pRoot->_pRight, blackCount, pathBlack);}Node* LeftMost(){//得到根節點Node* pRoot = GetRoot();if (nullptr == pRoot)return _pHead;Node* pCur = pRoot;//找到最左側結點while (pCur->_pLeft)pCur = pCur->_pLeft;return pCur;}Node* RightMost(){//得到根節點Node* pRoot = GetRoot();if (nullptr == pRoot)return _pHead;Node* pCur = pRoot;//找到最右側結點while (pCur->_pRight)pCur = pCur->_pRight;return pCur;}void RotateLeft(Node* pParent){Node* pSubR = pParent->_pRight;Node* pSubRL = pSubR->_pLeft;pParent->_pRight = pSubRL;if (pSubRL)pSubRL->_pParent = pParent;pSubR->_pLeft = pParent;Node* pPParent = pParent->_pParent;pParent->_pParent = pSubR;pSubR->_pParent = pPParent;if (pPParent == _pHead)GetRoot() = pSubR;else{if (pPParent->_pLeft == pParent)pPParent->_pLeft = pSubR;elsepPParent->_pRight = pSubR;}}void RotateRight(Node* pParent){Node* pSubL = pParent->_pLeft;Node* pSubLR = pSubL->_pRight;pParent->_pLeft = pSubLR;if (pSubLR)pSubLR->_pParent = pParent;pSubL->_pRight = pParent;Node* pPParent = pParent->_pParent;pParent->_pParent = pSubL;pSubL->_pParent = pPParent;//pParent是根結點if (pPParent == _pHead)GetRoot() = pSubL;else{//非根結點if (pPParent->_pLeft == pParent)pPParent->_pLeft = pSubL;elsepPParent->_pRight = pSubL;}}Node*& GetRoot()  //head是new出來的，head存在parent一定存在，按引用方式返回沒有問題{//得到根節點，也就是頭結點的下一個結點return _pHead->_pParent;}void _InOrder(Node* pRoot){if (pRoot){_InOrder(pRoot->_pLeft);cout << pRoot->_data << " ";_InOrder(pRoot->_pRight);}}
private:Node* _pHead;
};void TestRBTree()
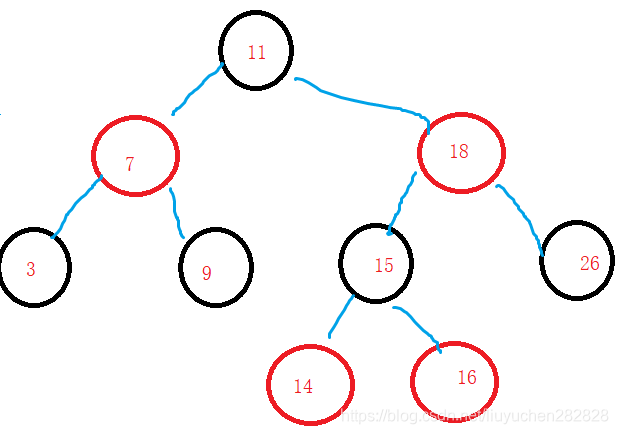
{int array[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };RBTree<int>t;for (auto e : array)t.Insert(e);t.InOrder();if (t.IsValidRBTree()){cout << "t is vaild rbTree" << endl;}elsecout << "t is not vaild rbTree" << endl;
}