排序的概念
- 排序:所謂排序,就是使一串記錄,按照其中的某個或某些關鍵字的大小,遞增或遞減的排列起來的操作。
- 穩定性:假定在待排序的記錄序列中,存在多個具有相同的關鍵字的記錄,若經過排序,這些記錄的相對次序保持不變,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,則稱這種排序算法是穩定的;否則稱為不穩定的。
- 內部排序:數據元素全部放在內存中的排序。
- 外部排序:數據元素太多不能同時放在內存中,根據排序過程的要求不能在內外存之間移動數據的排序。
常見的排序算法

基本思想
直接插入排序是一種簡單的插入排序法,其基本思想是:把待排序的記錄按其關鍵碼值的大小逐個插入到一個已經排好序的有序序列中,直到所有的記錄插入完為止,得到一個新的有序序列 。
直接插入排序
比如有手上有很多的牌,第一次抓一張牌出來,放到最前面,認為有序,第二次在抓一張牌出來和有序的牌中作比較,找到合適位置插入,依次類推。
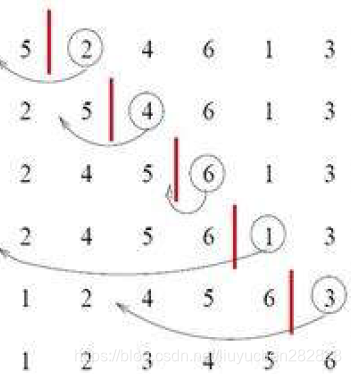
直接插入排序的特性總結:
- 元素集合越接近有序,數據量比較少,直接插入排序算法的時間效率越高
- 時間復雜度:O(N^2)
- 空間復雜度:O(1),它是一種穩定的排序算法
- 穩定性:穩定
算法實現
對于 3 2 5 8 4 7 6 9

對于這種情況
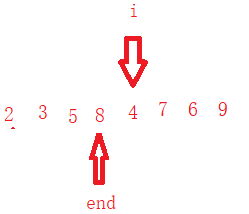
不斷重復重復第一次的操作就行,如果當前數比前一個數大,外循環就往后走
//2 4 5 9 3 6 8 7 1 0
for(int i=1;i<size;++i)
{int key =array[i];//保存當前數int end = i-1;while(key < array[end]&& end>=0){array[end+1] = array[end];//往后搬移end--;}array[end+1]=key
}
void InsertSort(int *array, int size)
{for (int i = 1; i < size; ++i){int key = array[i];int end = i - 1; //i前面的已經排好序了while (key < array[end] && end >= 0){array[end + 1] = array[end];end--;}array[end + 1] = key;}
}
希爾排序
希爾排序法又稱縮小增量法。希爾排序法的基本思想是:先選定一個整數,把待排序文件中所有記錄分成個組,所有距離為的記錄分在同一組內,并對每一組內的記錄進行排序。然后,取,重復上述分組和排序的工作。當到達=1時,所有記錄在統一組內排好序。
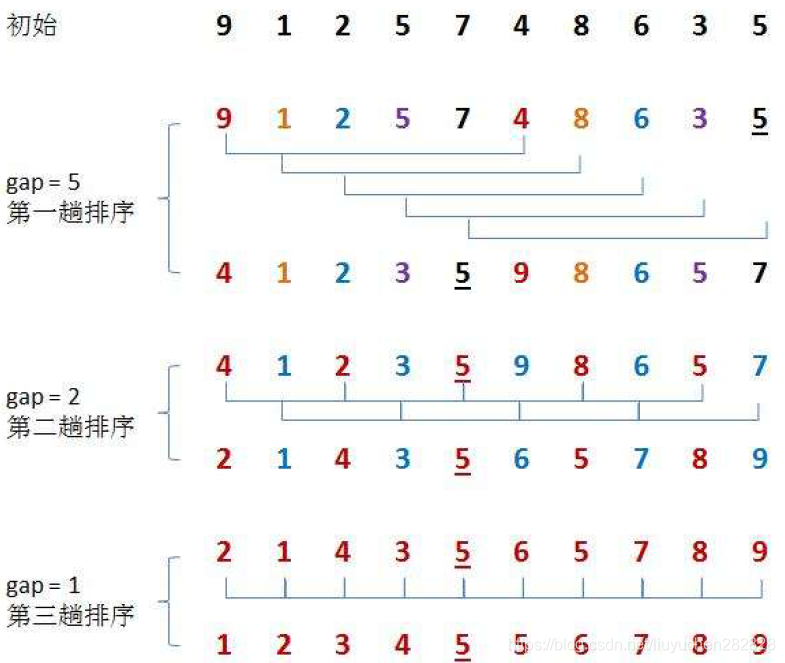
希爾排序的特性總結:
- 希爾排序是對直接插入排序的優化。
- 當gap > 1時都是預排序,目的是讓數組更接近于有序。當gap == 1時,數組已經接近有序的了,這樣就會很快。這樣整體而言,可以達到優化的效果。我們實現后可以進行性能測試的對比。
- 希爾排序的時間復雜度不好計算,需要進行推導,推導出來平均時間復雜度: O(N1.3—N2)沒有到O(N2)
- 穩定性:不穩定‘
void ShellSort(int* array, int size)
{int gap = size;while (gap > 1) {gap = gap / 3 + 1;for (int i = gap; i < size; ++i)//i每回加1,讓分組同時進行排序,不需要+gap{int key = array[i];int end = i - gap; //i的前一個元素while (key < array[end] && end >= 0){array[end + gap] = array[end];end -= gap;}array[end + gap] = key;} }
}
選擇排序
基本思想:
每一次從待排序的數據元素中選出最小(或最大)的一個元素,存放在序列的起始位置,直到全部待排序的數據元素排完 。
直接選擇排序:
- 在元素集合
array[i]--array[n-1]中選擇關鍵碼最大(小)的數據元素 - 若它不是這組元素中的最后一個(第一個)元素,則將它與這組元素中的最后一個(第一個)元素交換
- 在剩余的
array[i]--array[n-2](array[i+1]--array[n-1])集合中,重復上述步驟,直到集合剩余1個元素
直接選擇排序的特性總結:
- 直接選擇排序思考非常好理解,但是效率不是很好。實際中很少使用
- 時間復雜度:O(N^2)
- 空間復雜度:O(1)
- 穩定性:不穩定
代碼實現
void Swap(int *pLeft, int *pRight)
{int temp = *pLeft;*pLeft = *pRight;*pRight = temp;
}
//直接選擇排序
void SelectSort(int*array, int size)
{for (int i = 0; i < size - 1; ++i) //總共找多少次,-1是因為最后一次,區間中只有一個元素了{//找區間中最大元素的位置//找最大元素的方式int maxPos = 0; //找最大的元素for (int j = 1; j < size - i; ++j) //-i,從沒排序的序列中找最大的元素{if (array[j]>array[maxPos]) //如果大,下標變更maxPos = j;}if (maxPos != size - i - 1) //如果最大元素下標不等于此時當前沒排序區間的最后一個元素Swap(&array[maxPos], &array[size - i - 1]);//最大位置的元素和最后位置的元素交換}
}
直接選擇排序優化
一次排序時,找出當前區間,當前區間,當前區間最大和最小的元素,最大元素和當前區間的最后一個元素交換最小元素和當前區間第一個元素進行交換,交換完,區間縮小,重復操作,直到有序
//選擇排序優化
void SelectSort_OP(int*array, int size)
{int begin = 0;int end = size - 1;while (begin < end){int maxPos = begin;//認為當前區間第一個元素最大int minPos = begin;//認為當前區間第一個元素最小int i = begin;//i從當前區間第一個元素開始//在區間中找到最大和最小元素的位置while (i <= end){if (array[i]>array[maxPos])maxPos = i;if (array[i] < array[minPos])minPos = i;i++;}//最大和最小元素和當前區間第一位置和最后一位置進行交換if (maxPos != end)Swap(&array[maxPos], &array[end]);//交換的是下標里的值,下標并沒有改變//如果當前區間最后的元素放的正好是你找到最小元素,更新最小元素的位置if (minPos == end)minPos = maxPos;if (minPos != 0)Swap(&array[minPos], &array[begin]);//縮小區間begin++;end--;}
}
直接選擇排序的缺陷
每選一次都要從前往后再比一次
堆排序
堆的簡介與相關實現
堆排序的特性總結:
- 堆排序使用堆來選數,效率就高了很多。
- 時間復雜度:O(N*logN)
- 空間復雜度:O(1)
- 穩定性:不穩定
代碼實現
//O(logN)
void HeapAdjust(int*array, int size, int parent)
{int child = parent * 2 + 1; //左孩子//int right = parent * 2 + 2;//右孩子while (child<size){//找左右孩子中最大的if (child+1<size && array[child + 1] > array[child])child += 1;//檢測雙親是否滿足堆的性質if (array[child] > array[parent]) //不滿足{Swap(&array[child], &array[parent]);parent = child;child = parent * 2 + 1;}elsereturn;}
}//O(NlogN)
void HeapSort(int *array, int size)
{//建堆----升序(大堆) 降序(小堆)//從倒數第一個非葉子結點----向下調整//size-1數組中最后一個數,parent=(child-1)/2;int last = ((size - 1 - 1) / 2);for (; last >= 0; last)HeapAdjust(array, size, last--);//排序---堆的刪除int end = size - 1; //剩余排序的元素個數while (end){Swap(&array[0], &array[end]);HeapAdjust(array, end, 0);--end;}
}
)


















